AcWing 2. 01背包问题

\(AcWing ~ 2\) \(01\)背包

一、知识架构

\(01\)背包
\(N\)个物品，容量\(V\)的背包(上限)，\(w_i\)表示物品的体积,\(v_i\)表示价值
如何组装背包，在\(V\)的上限限制情况下，使得价值最大,求最大值。
总结：每个物品只有\(1\)个，可以选或不选，求在容量限制下的价值最大值。
完全背包
每个物品有无限个，求价值最大是多少。
多重背包
每个物品个数不一样，不是无限，也不是只有一个，有\(k_i\)的个数限制。
多重背包有一个二进制优化的扩展，称为 多重背包II ,就是打包策略。
分组背包
物品有\(n\)组，各一组有若干个。每一组最多选择一个物品，比如水果组选择了苹果，就不能选香蕉。
混合背包
物品一共有三类：
第一类物品只能用\(1\)次（\(01\)背包）；
第二类物品可以用无限次（完全背包）；
第三类物品最多只能用 \(s_i\) 次（多重背包）；

注意：不一定要装满背包

二、01背包的递归表示

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int res;

void dfs(int u, int r, int s) {
    if (u == n + 1) {
        res = max(res, s);
        return;
    }
    if (v[u] <= r) dfs(u + 1, r - v[u], s + w[u]);
    dfs(u + 1, r, s);
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    dfs(1, m, 0);
    printf("%d\n", res);
    return 0;
}

递归表示法的缺点：
因为有大量的重复计算，所以，不出意外的在大数据量的情况下，\(TLE\)了！我们需要找一个办法进行优化。

三、记忆化搜索

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
int n, m;
int w[N], v[N];
int f[N][N];

int dfs(int u, int r) {
    if (~f[u][r]) return f[u][r];
    if (u == n + 1) return 0;
    if (v[u] <= r)
        return f[u][r] = max(dfs(u + 1, r), dfs(u + 1, r - v[u]) + w[u]);
    return f[u][r] = dfs(u + 1, r);
}

int main() {
    memset(f, -1, sizeof f);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    printf("%d\n", dfs(1, m));
    return 0;
}

\(Q\):为什么记忆化搜索要以\(int\)返回，使用以前习惯的\(void\)返回不行吗？

让你失望了，如果\(dfs\)采用\(void\)作为返回值，是无法使用记忆化的：
因为我们利用每一次搜索的结果进而达到记忆化：之前搜过的就不用再搜了。

普通搜索的低效使得很多时候在数据比较大时会导致\(TLE\)，一个重要原因是其搜索过程中重复计算了重叠子问题。记忆化搜索以搜索的形式加上动态规划的思想，面对会有很多重复计算的问题时，在搜索过程中记录一些状态的答案，可以减少重复搜索量。记忆化搜索本质上是\(DP\)，它们都保存了中间结果，不同点是\(DP\)从下往上算，记忆化\(dfs\)因为是递归所以从上往下算。

记忆化搜索

递归函数的结果以返回值形式存在，不能以全局变量或参数形式传递
不依赖任何外部变量

（根据以上两个要求把朴素暴搜\(dfs\)写出来后，添加个记忆化数组就\(ok\)了）

记忆化数组一般初始化为\(-1\)。在每一状态搜索的开始进行判断，如果该状态已经计算过，则直接返回答案，否则正常搜索。

函数的参数表达的是：状态
函数的返回值表达的是:结果

策略与办法
如果对记忆化搜索不熟练，可以先写出\(void\)型\(dfs\)，再转化为有返回值的\(dfs\)，最后再加个数组记录已经搜过的状态就是记忆化\(dfs\)了。

四、二维数组法

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m;
int f[N][N];
int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;
        for (int j = 1; j <= m; j++) {
            f[i][j] = f[i - 1][j];
            if (j >= v)
                f[i][j] = max(f[i][j], f[i - 1][j - v] + w); // 两种情况取最大值
        }
    }

    printf("%d\n", f[n][m]);
    return 0;
}

五、一维数组法

为什么要用一维数组优化\(01\)背包问题
因为我们看到上面的存储方式，其实第\(i\)件物品选择或不选择两种方式，都只和\(i-1\)时的情况相关联，也就是说在\(i-1\)再以前的状态和数据与\(i\)无关，换句话说，就是没啥用了，可以清除掉了。这样一路走一路依赖它前面一行就OK，可以把二维数组优化为一维。

那么，怎么个优化法呢？答案是用一个一维数组。

这里最核心的问题是为什么容量的遍历要从大到小，和上面二维的不一样了呢？？
这是因为第\(i\)个要依赖于第\(i-1\)个，如果从小到大，那么\(i-1\)先变化了，而\(i\)说的依赖于\(i-1\)，其实是在没变化前的\(i-1\) 信息，这么直接来就错了。那怎么才能对呢？就是从大到小反向遍历，这样\(i-1\)都是以前的信息，还没变，就\(OK\)了！有点绕啊，但还算好理解！

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;

int n, m;
int f[N];

int main() {
    cin >> n >> m;

    // 01背包模板
    for (int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }
    printf("%d\n", f[m]);
    return 0;
}

七、\(01\)背包之恰好装满【扩展】

有\(n\)个体积和价值分别为\(v_i\),\(w_i\)的物品，现从这些物品中挑选出总体积恰好为 \(m\) 的物品，求所有方案中价值总和的最大值。

输入：包含多组测试用例，每一例的开头为两位整数 \(n、m\),\((1<=n<=10000,1<=m<=1000)\)，接下来有 \(n\) 行，每一行有两位整数 \(v_i、w_i(1<=v_i<=10000,1<=w_i<=100)\)。

输出：为一行，即所有方案中价值总和的最大值。若不存在刚好填满的情况，输出\(-1\)。

测试用例：

答案：

6
-1

恰好装满：

求最大值时，除了\(f[0]\)为\(0\)，其他都初始化为无穷小 -0x3f3f3f3f
求最小值时，除了\(f[0]\)为\(0\)，其他都初始化为无穷大 0x3f3f3f3f

不必恰好装满：
全初始化为\(0\)

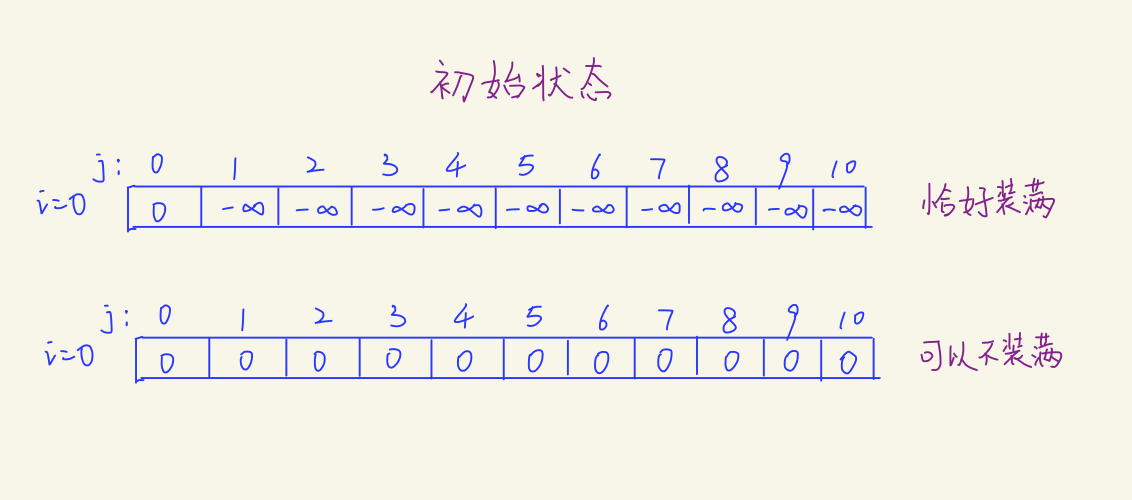
\(Q:\)为什么这样设置？

背包没恰好装满是无效状态， 恰好装满是有效状态。

当背包的状态为无效状态时，\(f[i]\)的值是\(-INF\)，这样就可以从状态转移矩阵中区分出有效状态和无效状态了。

回顾一下状态转移实现过程：

for (int j = 1; j <= m; j++) {
          f[i][j] = f[i - 1][j];
          if (j >= v)
              f[i][j] = max(f[i][j], f[i - 1][j - v] + w); //两种情况取最大值
      }

\(f[i][j]\) 的值是由 \(f[i - 1][j]，f[i - 1][j - w]\)来推导出来的，也就是 \(f[i][j]\) 的取值 只与前面的状态有关系,所有的状态都是从以前的状态来推导出来的。换句话说，所有的有效状态是从之前的有效状态和无效状态推导出来的！！！

目标：
通过初始化无效状态为\(-INF\),在不改变原来代码的情况下，解决掉恰好装满的问题！

我们来分析一下有效状态与无效状态之间的转化关系：

先上结论：

前序状态\(f[i - 1][j]\)	前序状态\(f[i - 1][j - w]\)	当前状态\(f[i][j]\)	转移来源
有效状态(满)	有效状态(满)	有效状态(满)	\(max(f[i-1][j],f[i-1][j-w]+v)\)
无效状态(不满)	有效状态(满)	有效状态(满)	\(max(f[i-1][j-w]+v,-INF)\)
有效状态(满)	无效状态(不满)	有效状态(满)	\(max(f[i-1][j],-INF)\)
无效状态(不满)	无效状态(不满)	无效状态(不满)	转不过来了 \(f[i][j] = max(f[i-1][j], f[i - 1][j - w] + v)\),\(-INF\)会被加上\(v\),不再是\(-INF\),但肯定是负数。

无效状态的处理方法

上面表格中也提到了这个问题：\(f[i][j] = max(f[i][j], f[i - 1][j - v] + w)\),如果两个前序状态都是无效状态，那么\(-INF\)会被加上\(w\),不再是\(-INF\),但肯定是负数。在最终结果判定中，我们可以认为是负数的，就是无效状态：假设负无穷不是靠你简单加上几个小正数就能大于零的~

二维代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n, m, f[N][N];

int main() {
    // 文件输入
    freopen("2_QiaHaoFill.in", "r", stdin);
    while (cin >> n >> m) {
        memset(f, -0x3f, sizeof(f));             // 其它位置全部初始化为-INF
        for (int i = 0; i < N; i++) f[i][0] = 0; // 第一列初始化为0

        for (int i = 1; i <= n; i++) {
            int w, v;
            cin >> v >> w;

            for (int j = v; j <= m; j++)
                f[i][j] = max(f[i][j], f[i - 1][j - v] + w);
        }
        if (f[n][m] < 0)
            puts("-1");
        else
            printf("%d\n", f[n][m]);
    }
    return 0;
}

一维代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 10010;

int n, m, f[N];
int main() {
    // 文件输入
    freopen("2_QiaHaoFill.in", "r", stdin);
    while (cin >> n >> m) {
        memset(f, -0x3f, sizeof(f));
        f[0] = 0;

        for (int i = 1; i <= n; ++i) {
            int v, w;
            cin >> v >> w;

            for (int j = m; j >= v; j--)
                f[j] = max(f[j], f[j - v] + w);
        }
        if (f[m] < 0)
            puts("-1");
        else
            printf("%d\n", f[m]);
    }
    return 0;
}

posted @ 2021-10-04 13:55 糖豆爸爸阅读(548) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

蒟蒻豆进阶之路

AcWing 2. 01背包问题