AcWing 861. 二分图的最大匹配
. 二分图的最大匹配
一、题目描述
给定一个二分图,其中左半部包含 个点(编号 ),右半部包含 个点(编号 ),二分图共包含 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配:给定一个二分图 ,在 的一个子图 中, 的边集 中的任意两条边都不依附于同一个顶点,则称 是一个匹配。
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 、 和 。
接下来 行,每行包含两个整数 和 ,表示左半部点集中的点 和右半部点集中的点 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
,
输入样例:
2 2 4
1 1
1 2
2 1
2 2
输出样例:
2
二、二分图的最大匹配
-
前提:给定一个二分图,不用你判断是不是二分图,已经明确知道是二分图,让你求它的最大匹配。
-
定义:在一个无向图中,定义一条边覆盖的点为这条边的两个端点。
找到一个边集包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。的大小叫做图的最大匹配。
匈牙利算法
又名:【月佬算法】,目标:成就更多美满姻缘!
建立有向图,分为二分图的左侧和右侧。 优先选择左侧序号更小的连接可能的边。 对于两个点的目标点“冲突”的时候,采取“协商”的办法。 即序号小的连接可能连接的另一条边。 若“协商”失败,则放弃序号较大的点的边。
概念看的都好绕,实例比较好懂:
你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
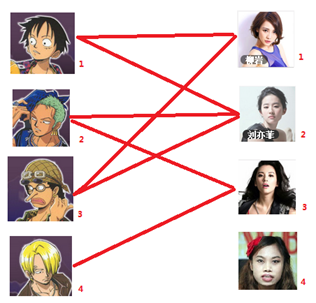
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
- 先试着给号男生找妹子,发现第一个和他相连的号女生还名花无主,,连上一条蓝线
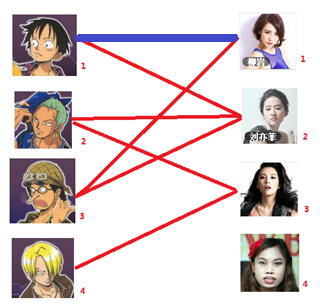
- 接着给号男生找妹子,发现第一个和他相连的号女生名花无主,
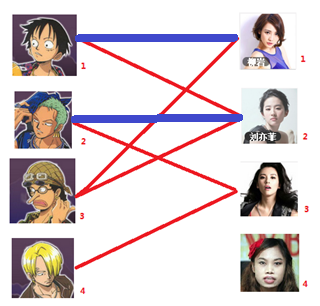
- 接下来是号男生,很遗憾号女生已经有主了,怎么办呢?
我们试着给之前号女生匹配的男生(也就是号男生)另外分配一个妹子。(黄色表示这条边被临时拆掉)
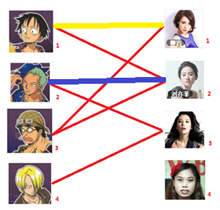
与号男生相连的第二个女生是号女生,但是号女生也有主了,怎么办呢?我们再试着给号女生的原配重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
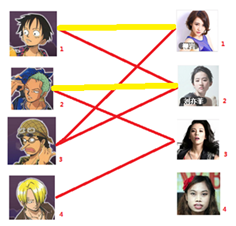
此时发现号男生还能找到号女生,那么之前的问题迎刃而解了,回溯回去
| 号男生可以找号妹子 | 号男生可以找号妹子 | 号男生可以找号妹子 |
|---|---|---|
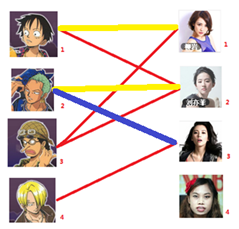 |
 |
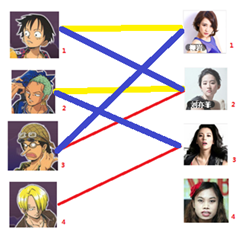 |
所以第3步最后的结果就是:
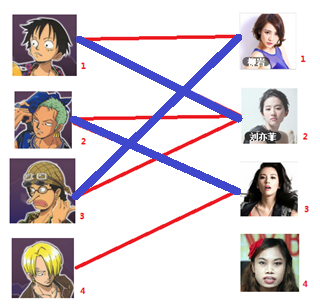
- 接下来是号男生,很遗憾,按照第三步的节奏我们没法给号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
const int M = 100010;
int n1, n2;
int m;
int match[N];
int st[N];
int res;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!st[v]) {
st[v] = 1;
if (match[v] == 0 || dfs(match[v])) {
match[v] = u;
return 1;
}
}
}
return 0;
}
int main() {
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
while (m--) {
int a, b;
cin >> a >> b;
add(a, b);
}
for (int i = 1; i <= n1; i++) {
memset(st, 0, sizeof st);
if (dfs(i)) res++;
}
printf("%d\n", res);
return 0;
}
五、 解释int st[N]的作用
重点:st[]的作用:
首先我们 遍历属于的单链表相当于遍历他所有喜欢的女生
如果某个女生没有被他预定过的话,就标记这个女生被他预定,即
这时如果女还没有匹配过,即的时候,那这个预定就成真了,得到
而如果女之前就被男匹配过了,那我们就,也就是(因为原本)
然后在的过程中,因为,这时候男就不能再选则女了,因为女已经被预定了,所以男就只能在他喜欢的女生里面选择其他人来匹配。
当然,如果返回的话,那就 都不成立,那男就一边玩去吧~



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2017-09-26 使用GitLab进行落地项目的管理,并且自动更新、重启、回滚
2017-09-26 利用ssh反向代理以及autossh实现从外网连接内网服务器
2017-09-26 升级PIP源