AcWing 860. 染色法判定二分图

\(AcWing\) \(860\). 染色法判定二分图

一、题目描述

给定一个 \(n\) 个点 \(m\) 条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式
第一行包含两个整数 \(n\) 和 \(m\)。

接下来 \(m\) 行，每行包含两个整数 \(u\) 和 \(v\)，表示点 \(u\) 和点 \(v\) 之间存在一条边。

输出格式
如果给定图是二分图，则输出 Yes，否则输出 No。

数据范围
\(1≤n,m≤10^5\)

输入样例：

4 4
1 3
1 4
2 3
2 4

输出样例：

Yes

二、二分图的概念

二分图,是图论中的一种特殊模型，设\(G=(V,E)\)是一个无向图，如果顶点\(V\)可分割为 两个互不相交的子集 \((A,B)\)，并且同一集合中不同的两点没有边相连,就是二分图。

举个栗子吧：

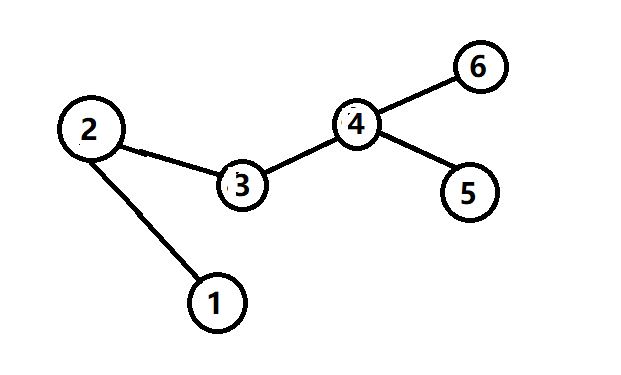
这是不是二分图？
反正我第一次看觉得不是。其实，是的，他是二分图，尽管看上去是连着的。
若我们将图中的一些边转一下，变成：

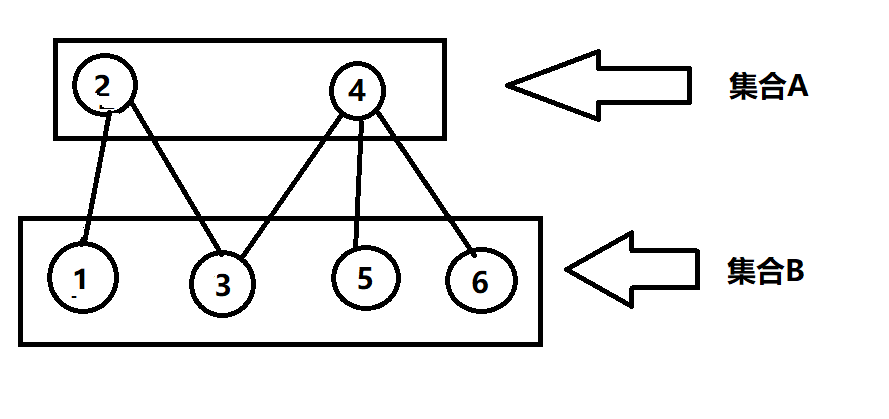
这就是一个明显的二分图。集合A与B中的点互不相连!。

只要两个点之间有边，那么这两个点就不能同属一个集合，必须分在两边。

三、二分图的几个性质

• 二分图不一定是连通图

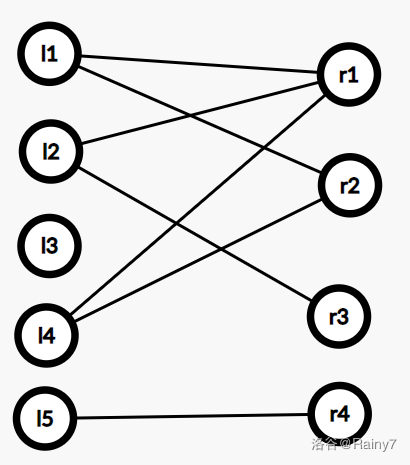
• 一定不含有奇数环，可以包含长度为偶数的环
  

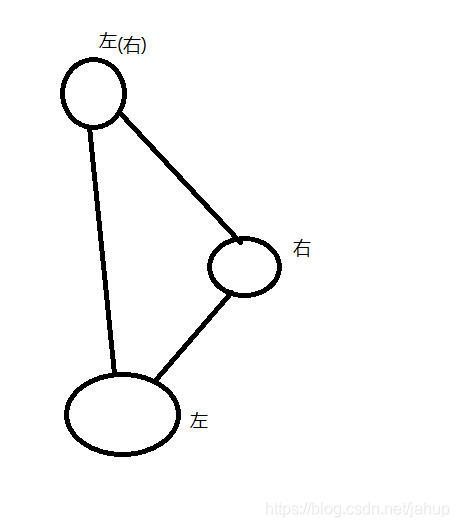
• 任何无回路的图均是二分图

四、\(DFS\)实现

染色法是判断二分图的办法：

#include <bits/stdc++.h>

using namespace std;
const int N = 100010, M = N << 1;

int n, m;
int color[N];

// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

// u:点 c:颜色值
bool dfs(int u, int c) {
    color[u] = c;
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (!color[v]) {                  // 没有染色过
            if (!dfs(v, 3 - c)) return 0; // 这个3-c用的太妙了
        } else if (color[v] == c)
            return 0; // 染色冲突
    }
    return 1;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;

    while (m--) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    bool flag = 1;
    for (int i = 1; i <= n; i++)
        if (!color[i]) { // 把当前点染色为1
            if (!dfs(i, 1)) {
                flag = 0;
                break;
            }
        }
    if (flag)
        puts("Yes");
    else
        puts("No");
    return 0;
}

五、\(BFS\)实现

#include <bits/stdc++.h>

using namespace std;
const int N = 100010, M = N << 1;
typedef pair<int, int> PII;

int n, m;
int color[N];
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs(int x) {
    // 假设 1:黑，2：白，这样方便理解一些
    color[x] = 1;
    queue<PII> q;
    q.push({x, 1});
    while (q.size()) {
        PII t = q.front();
        q.pop();
        int u = t.first, c = t.second;
        for (int i = h[u]; ~i; i = ne[i]) {
            int v = e[i];
            if (!color[v]) {
                color[v] = 3 - c;
                q.push({v, 3 - c});
            } else if (color[v] == c) // 发现冲突
                return 0;
        }
    }
    return 1;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    int a, b;
    while (m--) {
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    int flag = 1;
    for (int i = 1; i <= n; i++) {
        if (!color[i]) {
            if (!bfs(i)) {
                flag = 0;
                break;
            }
        }
    }
    if (flag)
        puts("Yes");
    else
        puts("No");
    return 0;
}