AcWing 854. Floyd求最短路

\(AcWing\) \(854\). \(floyd\) 求最短路

一、题目描述

给定一个 \(n\) 个点 \(m\) 条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 \(k\) 个询问，每个询问包含两个整数 \(x\) 和 \(y\)，表示查询从点 \(x\) 到点 \(y\)的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。

输入格式
第一行包含三个整数 \(n,m,k\)。

接下来 \(m\) 行，每行包含三个整数 \(x,y,z\)，表示存在一条从点 \(x\) 到点 \(y\) 的有向边，边长为 \(z\)。

接下来 \(k\) 行，每行包含两个整数 \(x,y\)，表示询问点 \(x\) 到点 \(y\) 的最短距离。

输出格式
共 \(k\) 行，每行输出一个整数，表示询问的结果，若询问两点间不存在路径，则输出 impossible。

数据范围
\(1≤n≤200,1≤k≤n^2,1≤m≤20000\),
图中涉及边长绝对值均不超过 \(10000\)。

输入样例：

3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3

输出样例：

impossible
1

二、理解和感悟

1. \(Floyd\)可以求多源最短路径，这是其它算法做不到的。
   

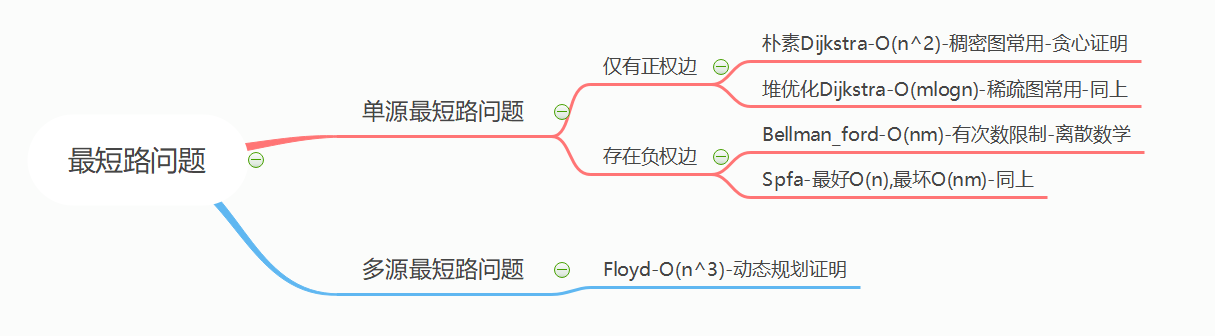
2. \(Floyd\)可以处理负权边，但不能处理负权回路。

3. 核心就是初始化+三重循环，注意顺序是\(k-i-j\)，不能反了！\(Floyd\)是有动态规划思想的算法。

原理解析：
\(f[k][i][j]\)表示\(i\)和\(j\)之间可以通过编号为\(1..k\)的节点的最短路径
初值\(f[0][i][j]\)为原图的邻接矩阵

• \(i\)到\(j\)不经过\(k\)这个节点: \(f[k][i][j]\)可以从\(f[k-1][i][j]\)转移
• \(i\)到\(j\)经过\(k\)这个节点: 从\(f[k-1][i][k]+f[k-1][k][j]\)转移

即\(f[k][i][j]=min(f[k-1][i][j],f[k-1][i][k]+f[k-1][k][j])\)

然后你就会发现最外层一维空间可以省略，因为\(f[k]\)只\(f[k-1]\)与有关。

总结：
一句话，\(Floyd\)算法的本质是\(DP\)，而\(k\)是\(DP\)的阶段，因此要写最外面。

三、实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 210;
const int INF = 0x3f3f3f3f;

int n, m, k;
int d[N][N];

// 算法结束后，d[a][b]表示a到b的最短距离
void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    cin >> n >> m >> k;
    // floyd初始化
    memset(d, 0x3f, sizeof d);               // 任意两点间距离正无穷
    for (int i = 0; i < N; i++) d[i][i] = 0; // 自己和自己是距离为0的
    // 读入数据
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c); // 保留最短边.(可能有重边，保留最短边)
    }
    // 调用floyd
    floyd();

    // 处理所有询问
    while (k--) {
        int a, b;
        cin >> a >> b;
        // 由于有负权边存在所以约大过INF/2也很合理
        if (d[a][b] > INF / 2)
            puts("impossible");
        else
            printf("%d\n", d[a][b]);
    }
    return 0;
}