AcWing 849. Dijkstra求最短路 I

\(AcWing\) \(849\). \(Dijkstra\)求最短路 \(I\)

一、题目描述

给定一个 \(n\) 个点 \(m\) 条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 \(1\) 号点到 \(n\) 号点的最短距离，如果无法从 \(1\) 号点走到 \(n\) 号点，则输出 \(−1\)。

输入格式
第一行包含整数 \(n\) 和 \(m\)。

接下来 \(m\) 行每行包含三个整数 \(x,y,z\)，表示存在一条从点 \(x\) 到点 \(y\) 的有向边，边长为 \(z\)。

输出格式
输出一个整数，表示 \(1\) 号点到 \(n\) 号点的最短距离。

如果路径不存在，则输出 \(−1\)。

数据范围
\(1≤n≤500,1≤m≤10^5\),图中涉及边长均不超过\(10000\)。

输入样例：

3 3
1 2 2
2 3 1
1 3 4

输出样例：

3

二、算法思路

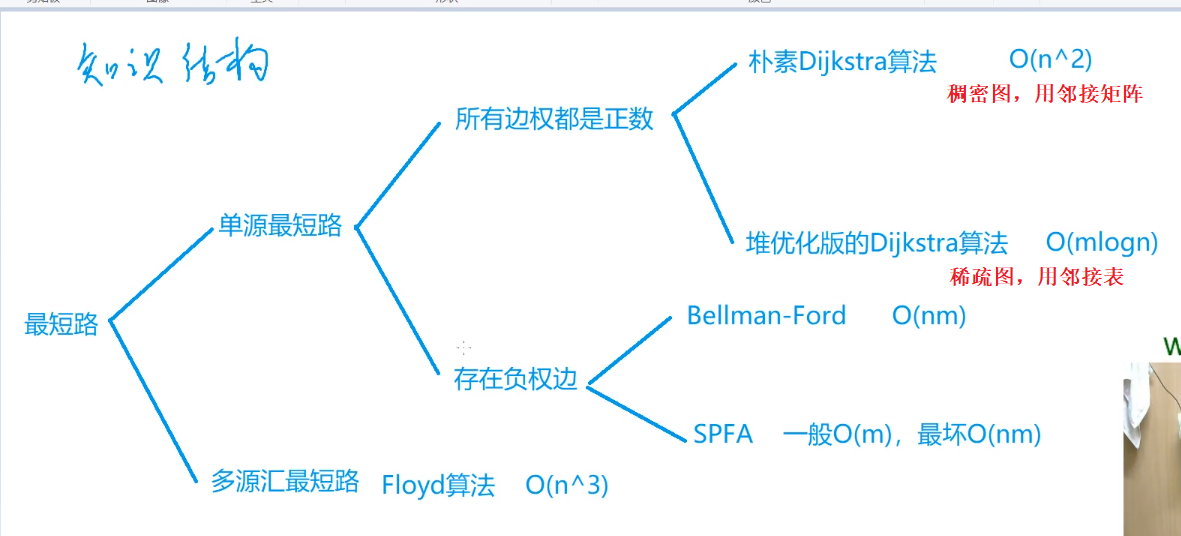
\(Dijkstra\) 的整体思路比较清晰,即进行\(n\)次迭代去确定每个点到起点的最小值,最后输出的终点的即为我们要找的最短路的距离。

按照这个思路除了存储图外我们还需要存储两个量:

dist[n]   //用于存储每个点到起点的最短距离
st[n]     //用于在更新最短距离时 判断当前的点的最短距离是否确定 是否需要更新

每次迭代的过程中我们都 先找到当前未确定的最短距离的点中距离最短的点,（至于为什么是这样那么这就涉及到\(Dijkstra\)算法的具体数学证明了 有兴趣的同学可以百度一下）

int t=-1;                                 //将t设置为-1 因为Dijkstra算法适用于不存在负权边的图
for(int j=1;j<=n;j++){
    if(!st[j]&&(t==-1||dist[t]>dist[j])    //该步骤即寻找还未确定最短路的点中路径最短的点
        t=j;
}

通过上述操作当前我们的\(t\)代表就是剩余未确定最短路的点中路径最短的点,而与此同时该点的最短路径也已经确定我们将该点标记:

st[t]=true;

然后用这个去更新其余未确定点的最短距离

进行\(n\)次迭代后最后就可以确定每个点的最短距离,然后再根据题意输出相应的要求的最短距离。

二、实现代码【这个代码不用背，直接背带堆优化版本的】

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 510;
const int M = 1e5 + 10;
int n, m;

//邻接表
int h[N], w[M], e[M], ne[M], idx;
bool st[N];  //是否使用过
int dist[N]; //最短距离数组

//维护邻接表
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int dijkstra() {
    memset(dist, 0x3f, sizeof dist); //初始化为无穷大
    dist[1] = 0;                     //出发点的距离初始化为0

    for (int i = 0; i < n; i++) {
        //找到距离出发点最近的点
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;

        st[t] = true;
        for (int j = h[t]; ~j; j = ne[j]) {
            int k = e[j];
            dist[k] = min(dist[k], dist[t] + w[j]);
        }
    }
    return dist[n] == INF ? -1 : dist[n];
}

int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    //调用迪卡斯彻算法
    int t = dijkstra();
    printf("%d\n", t);
    return 0;
}