AcWing 846. 树的重心

\(AcWing\) \(846\). 树的重心

一、题目描述

给定一颗树，树中包含 \(n\) 个结点（编号 \(1∼n\)）和 \(n−1\) 条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式
第一行包含整数 \(n\)，表示树的结点数。

接下来 \(n−1\) 行，每行包含两个整数 \(a\) 和 \(b\)，表示点 \(a\) 和点 \(b\) 之间存在一条边。

输出格式
输出一个整数 \(m\)，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围
\(1≤n≤10^5\)

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例：

4

二、题意分析

1. 什么树重心？

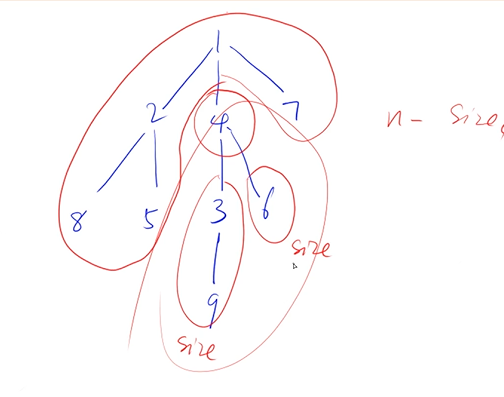
重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

树的重心不一定只是一个，有时可以是两个。

2. 如何求树的重心
在树上可以进行两种遍历：深度、广度。其中深度遍历可以模拟一支笔在树上画线，直至遍历完成所有节点。我们可以利用这一特点，让每个大臣分派出任务时，都要求下一级的官员返回自己管辖范围内的结点数。然后它自己负责把下级返回的个数加在一起，再加上自己的结点数1，返回给上级调用者。

三、实现代码

#include <bits/stdc++.h>

using namespace std;
const int N = 100010, M = 200010;
const int INF = 0x3f3f3f3f;
int ans = INF;
bool st[N];
int n;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int dfs(int u) {
    st[u] = 1;
    int sum = 1;
    int res = 0;
    for (int i = h[u]; ~i; i = ne[i]) {
        int v = e[i];
        if (!st[v]) {
            int s = dfs(v);    // v子树有多少个节点
            sum += s;          // 儿子们的节点个数累加和,再加自己的1，就是u子树的节点个数sum和
            res = max(res, s); // 猴子选大王
        }
    }
    res = max(res, n - sum); // 套路:除了自己的所有猴子，还要考虑反向子树
    ans = min(ans, res);     // 最大中选最小，就是树的重心
    return sum;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n;                     // n个顶点
    for (int i = 1; i < n; i++) { // n-1条边
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    dfs(1);
    cout << ans << endl;
    return 0;
}