AcWing 835. Trie字符串统计

\(AcWing\) \(835\). \(Trie\)字符串统计

一、题目描述

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 \(x\)；
Q x 询问一个字符串在集合中出现了多少次。

共有 \(N\) 个操作，所有输入的字符串总长度不超过 \(10^5\)，字符串仅包含小写英文字母。

输入格式
第一行包含整数 \(N\)，表示操作数。

接下来 \(N\) 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式
对于每个询问指令Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围
\(1≤N≤2∗10^4\)

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

二、什么是\(Trie\)树

\(Trie\)树又称字典树、单词查找树。是一种能够高效存储和查找字符串集合的数据结构。咋看之下不是很复杂，但是仔细看代码又有点模糊。储存形式如下：

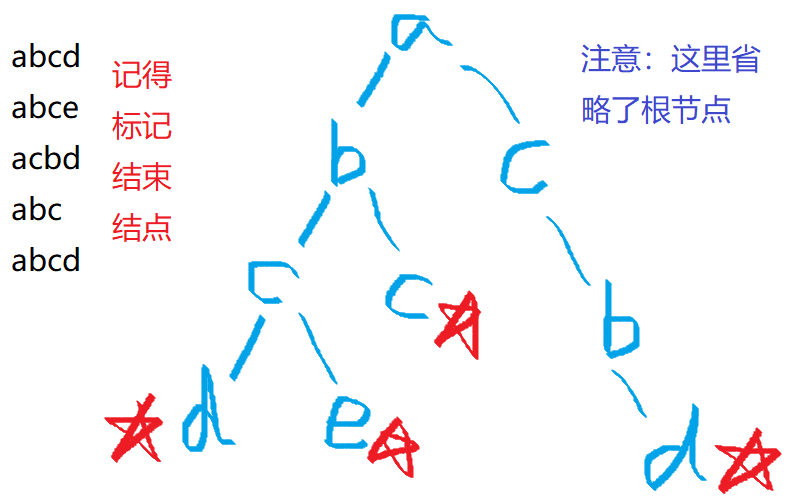
总结

• \(tr[N][26]\)来描述\(Trie\)树，第一维是构建\(Trie\)树的字符串的总长度，第二维是指\(a\sim z\)共26种可能。

• \(tr[i][j]=k\)是指节点\(i\)通过\(j\)这条边（比如\(a\),就是\(j=0\),\(b\)就是\(j=1\)...），值\(k\)是指到达了哪个子节点。

\(Trie\) 树的以下几个特点：

具有相同前缀的词必须位于同一个串内；例如“清华”、“清新”两个词都有“清”这个前缀，那么在 \(Trie\) 树上只需构建一个“清”节点，“华”和“新”节点共用一个父节点即可，如此两个词便只需三个节点便可存储，这在一定程度上减少了字典的存储空间。

\(Trie\) 树中的词只可共用前缀，不可共用词的其他部分；例如“中华”、“华人”这两个词虽然前一个词的后缀是后一个词的前缀，但在树形上必须是独立的两条链路，而不可以通过首尾交接构建这两个词，这也说明 \(Trie\) 树仅能依靠公共前缀压缩字典的存储空间，并不能共享词中的所有相同的字符；当然，这一点也有“例外”，对于复合词，可能会出现两词首尾交接的假象，比如“清华大学”这个词在上例 \(Trie\) 树中看起来似乎是由“清华”、“大学”两词首尾交接而成，但是叶子节点的标识已经明确说明 \(Trie\) 树里面只有”清华“和”清华大学“两个词，它们之间共用了前缀，而非由“清华”和”大学“两词首尾交接所得，因此上例 \(Trie\) 树中若需要“大学”这个词则必须从根节点开始重新构建该词。

\(Trie\) 树中任何一个完整的词，都必须是从根节点开始至叶子节点结束，这意味着对一个词进行检索也必须从根节点开始，至叶子节点才算结束。

三、本题答案

#include <bits/stdc++.h>

using namespace std;
const int N = 1e5 + 10;
int tr[N][26], idx, cnt[N];

void insert(string str) {
    int p = 0;
    for (int i = 0; i < str.size(); i++) {
        int u = str[i] - 'a';
        if (!tr[p][u]) tr[p][u] = ++idx;
        p = tr[p][u];
    }
    cnt[p]++;
}

int query(string str) {
    int p = 0;
    for (int i = 0; i < str.size(); i++) {
        int u = str[i] - 'a';
        if (!tr[p][u]) return 0;
        p = tr[p][u];
    }
    return cnt[p];
}

int main() {
    int n;
    cin >> n;
    while (n--) {
        char op;
        string str;
        cin >> op >> str;
        if (op == 'I')
            insert(str);
        else
            printf("%d\n", query(str));
    }
    return 0;
}