AcWing 802. 区间和
. 区间和
一、题目描述
假定有一个无限长的数轴,数轴上每个坐标上的数都是 。
现在,我们首先进行 次操作,每次操作将某一位置 上的数加 。
接下来,进行 次询问,每个询问包含两个整数 和 ,你需要求出在区间 之间的所有数的和。
输入格式
第一行包含两个整数 和 。
接下来 行,每行包含两个整数 和 。
再接下来 行,每行包含两个整数 和 。
输出格式
共 行,每行输出一个询问中所求的区间内数字和。
数据范围
,
,
,
输入样例:
3 3
1 2
3 6
7 5
1 3
4 6
7 8
输出样例:
8
0
5
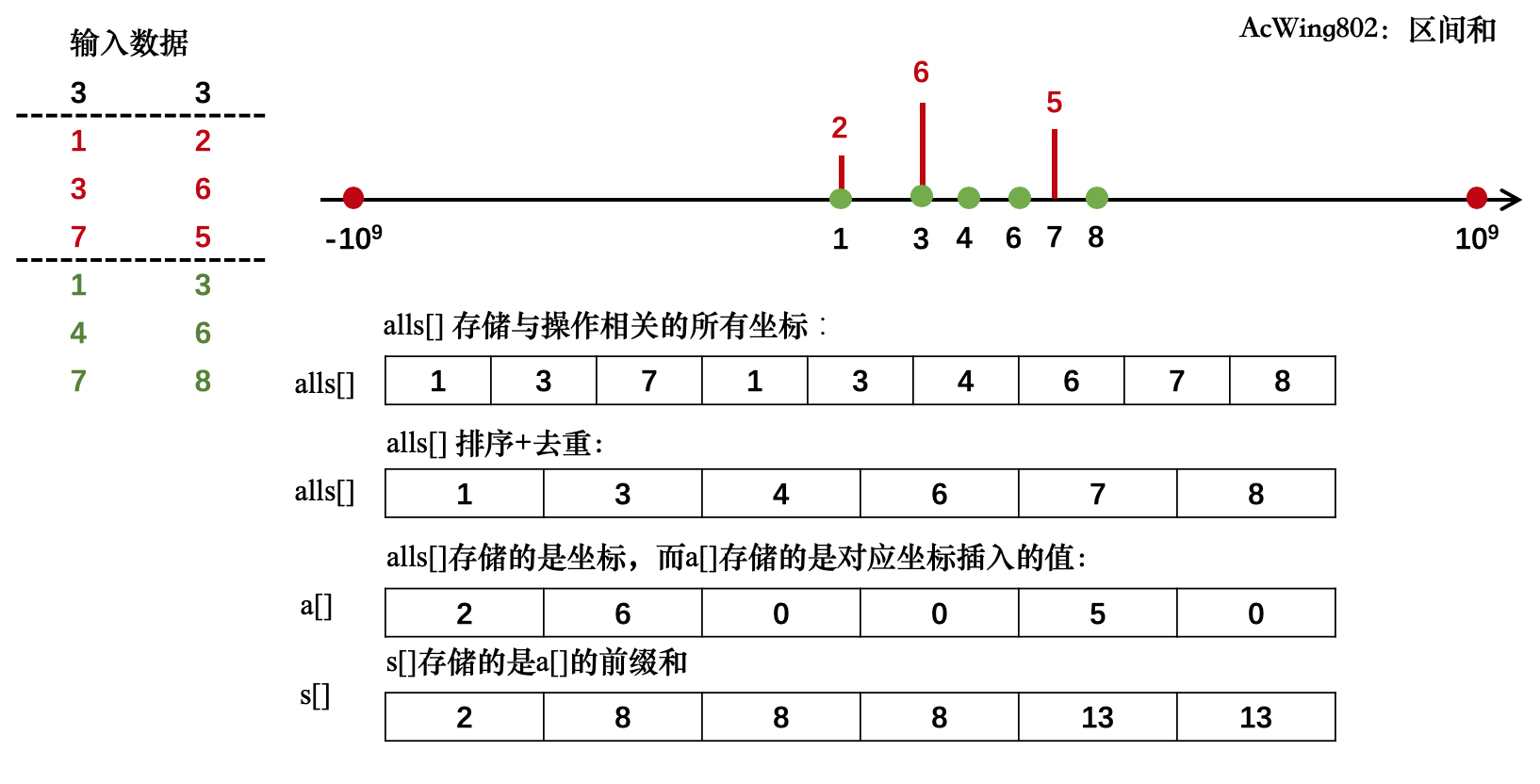
特殊说明一下,数组下标是从开始的,而数组下标是从开始的,数组与数组是一一对应的,但是错位对应的,即
二、解题思路
-
为什么要离散化?
因为 空间上不允许开那么大数据范围的数组 !本题,,两边都加上就是,开不到以上,空间超限。 -
什么是离散化?
离散化:范围大,但比较稀疏,真正有数的不多,很多地方是空着的(空着的是0)。利用这一特点,把有用的位置 映射 到一个长度可控的范围上。 -
数组大小的确定
既然要映射到一块小的、能装的下的区域内,那么这个区域最大是多大呢?
因为原始数据坐标共个,而查询时坐标是,一次两个,一共次,需要把所有的坐标全部放到数组中,上限是:,依题意,就是 -
离散化模板
// ① 排序+去重
sort(a, a + al);
// ② 使用STL的去重函数去重,不用手写的去重,原因:只排序一次,去重一次,不像是二分需要重复使用,性能差另不大,但代码就短的多
al = unique(a, a + al) - a;
三、模板代码
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 300010;
int a[N], al;
int b[N], s[N]; // 假定有一个无限长的数轴,数轴上每个坐标上的数都是 0
PII q[N], p[N];
int ql, pl;
int n, m;
// 手写二分
int lower_bound(int q[], int l, int r, int x) {
while (l < r) {
int mid = (l + r) >> 1;
if (q[mid] >= x)
r = mid;
else
l = mid + 1;
}
return l;
}
int main() {
cin >> n >> m;
while (n--) {
int x, c;
cin >> x >> c;
p[pl++] = {x, c};
a[al++] = x;
}
int l, r;
while (m--) {
cin >> l >> r;
q[ql++] = {l, r};
a[al++] = l, a[al++] = r;
}
// ① 排序+去重
sort(a, a + al);
// ② 使用STL的去重函数去重,不用手写的去重,原因:只排序一次,去重一次,不像是二分需要重复使用,性能差别不大,但代码就短的多
al = unique(a, a + al) - a;
// 处理一下某个x上加c的事情
for (int i = 0; i < pl; i++) {
int x = lower_bound(a, 0, al, p[i].first) + 1; // 下标从0开始,需要加1个偏移量
b[x] += p[i].second;
}
// 一维前缀和
for (int i = 1; i < N; i++) s[i] = s[i - 1] + b[i];
// 处理询问(前缀和应用)
for (int i = 0; i < ql; i++) {
// 根据原来的位置值,计算出映射后的位置值
l = lower_bound(a, 0, al, q[i].first) + 1;
r = lower_bound(a, 0, al, q[i].second) + 1;
// 利用一维前缀和计算区间和
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}
四、总结
- 提到的所有位置点,不管是有数值的点,还要是查询的点,统统记录到数组中
- 对数组进行排序+去重操作
- 遍历每一个有值的点,通过二分将原坐标变换为新的坐标,使用一个基础数组,记录新坐标中对应的数值
- 对基础数组生成前缀和数组
- 利用前缀和数组回答问题
五、完全使用的代码实现
因为多次调用二分算法,手工与的性能差距放大了~
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 300010;
int a[N], al;
int b[N], s[N]; // 假定有一个无限长的数轴,数轴上每个坐标上的数都是 0
PII q[N], p[N];
int ql, pl;
int n, m;
int main() {
cin >> n >> m;
while (n--) {
int x, c;
cin >> x >> c;
p[pl++] = {x, c};
a[al++] = x;
}
int l, r;
while (m--) {
cin >> l >> r;
q[ql++] = {l, r};
a[al++] = l, a[al++] = r;
}
// ① 排序+去重
sort(a, a + al);
// ② 使用STL的去重函数去重,不用手写的去重,原因:只排序一次,去重一次,不像是二分需要重复使用,性能差别不大,但代码就短的多
al = unique(a, a + al) - a;
// 处理一下某个x上加c的事情
for (int i = 0; i < pl; i++) {
int x = lower_bound(a,a+ al, p[i].first)-a + 1; // 下标从0开始,需要加1个偏移量
b[x] += p[i].second;
}
// 一维前缀和
for (int i = 1; i < N; i++) s[i] = s[i - 1] + b[i];
// 处理询问(前缀和应用)
for (int i = 0; i < ql; i++) {
// 根据原来的位置值,计算出映射后的位置值
l = lower_bound(a, a+ al, q[i].first)-a + 1;
r = lower_bound(a, a+ al, q[i].second)-a + 1;
// 利用一维前缀和计算区间和
printf("%d\n", s[r] - s[l - 1]);
}
return 0;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2017-09-08 Python3发送qq邮件,测试通过