P2789 直线交点数

题目传送门

我们将$n$条直线编号,分别称为直线$1$、直线$2$、…、直线$n$。直线$2$ 与直线$1$ 最多有一个交点，直线$3$与直线$1$和直线$2$最多有$2$个交点，……，直线$n$与其它 $(n-1)$ 条直线最多 $(n-1)$ 个交点。

由此看出,$n$条无三线共点的直线最多的交点数 $max=1+2+…+(n-1)=n(n-1)/2$。

但本题我们要求解的是：这 $n$ 条直线共有多少种不同的交点数？ 仍然从举例出发。下面列举了 $n=1、2、3、4$ 四种情况各自的交点情况：

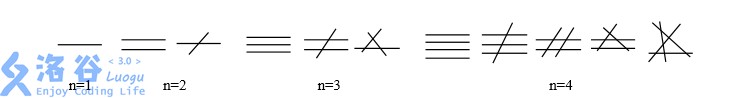
具体分析一下 $n=4$ 的情况：

已确定的交点数量:$sum$,待确定的直线条数:$p$,可能造成的交点数：$g(int\ p,int\ sum)$

分情况讨论（对照上面的图）：

• $4$条直线平行，则$0$个交点。

• $3$条直线平行，则$1 \times 3=3$个交点。

• $2$条直线平行，则这$2$条直线与另$2$条直线的交点数为$2 \times 2=4$, 而另外$2$条直线之间可能有$0$个或$1$个交点 （见 $n=2$ 的情况),共 $4$ 个交点或 $5$ 个交点。其实这里面的$4$就是前面的调用者把自己知道的已知交点数量做为小纸条传递给下一个分身，让它继续探索到结束。

• $4$条直线均不平行（可看成 $1$ 条直线平行），这 $1$ 条直线与其它 $3$ 条直线的交点数为 $3$，而其它 $3$条直线之间的交点数为，共$6$个交点。

经过以上分析，我们可以得如下结论：

$p$条直线的交点方案=$r$条平行线与$（p-r）$条直线交叉的交点数+（p-r）条直线本身的交点方案

=$r\times (p-r)$+$(p-r)$条直线本身的交点方案 $（1<=r<=p）$

#include <bits/stdc++.h>

using namespace std;
//https://www.luogu.com.cn/blog/user34320/solution-p2789
using namespace std;
const int N = 310;
bool visit[N];
/**
 对p条直线分情况讨论平行线的条数，已知在有r条平行线时有（p-r）条线与他们相交于p*（p-r）个交点，
 再加上对于这p-r个交点的相交组合即可！！！
 */
/**
 * 功能：讨论处理n条线的交点数情况有哪些
 * @param p n条线
 * @param sum 已经确定的交点数量
 */
void g(int p, int sum) {
    //标记k个结点数量是存在的
    visit[sum] = true;
    //递归出口，如果0条直线，就返回吧
    if (p == 0) return;
    //n条直线中，存在的平行线条数，需要逐个遍历一遍
    for (int r = p; r >= 1; r--)
        g(p - r, r * (p - r) + sum);
}

int main() {
    //输入
    int n, ans;
    cin >> n;
    //从n条直线，交点数量为0（全部平行）开始讨论
    g(n, 0);
    //统计结果
    for (int i = 0; i < N; i++) ans += visit[i];
    //输出结果
    cout << ans;
    return 0;
}