一、什么是德.摩根定律
德摩根定律有多种形式,在集合中的形式如下:
我们可以用生活中的例子也来理解该定理,假设某学校举办运动会,A 代表“去跑步”的同学,B 代表“去跳远”的同学,A∪B 表示“去跑步或跳远”的同学,所以有:
而A∩B 表示“既跑步又跳远”,所以有:
二、怎么记忆摩根定律
理解归理解,德摩根定律看上去还是有点复杂,可以通过下面方法来记忆,就是头顶上的帽子断开时,中间的符号要翻转:
德摩根定律拓展到多个事件上也是成立的,记忆方法也是一样的:
三、小试牛刀
化简下面的逻辑表达式:
1、 (A+B)(A+C)
=AA+AC+AB+BC 分配律
=A+AC+AB+BC AA=A
=A(1+C+B)+BC 反向使用分配律
=A+BC A+1=1
结论:(A+B)(A+C)=A+BC
2、AB+¯¯¯¯AC+BC
=AB+¯¯¯¯AC+BC(A+¯¯¯¯A) 依据:A+¯¯¯¯A=1
=AB+¯¯¯¯AC+ABC+¯¯¯¯ABC 分配律
=AB+ABC+¯¯¯¯AC+¯¯¯¯ABC 结合律
=AB(1+C)+¯¯¯¯AC(1+B) 反向分配律
=AB+¯¯¯¯AC A+1=1
结论:AB+¯¯¯¯AC+BC=AB+¯¯¯¯AC
3、¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A¯¯¯¯B+¯¯¯¯¯¯¯¯AC
=(¯¯¯¯A+B)(A+C) 摩根定律
=¯¯¯¯AA+¯¯¯¯AC+AB+BC 分配律
=AB+¯¯¯¯AC+BC A¯¯¯¯A=0
=AB+¯¯¯¯AC+BC(A+¯¯¯¯A) 依据:A+¯¯¯¯A=1
=AB+¯¯¯¯AC+ABC+¯¯¯¯ABC 分配律
=AB+ABC+¯¯¯¯AC+¯¯¯¯ABC 结合律
=AB(1+C)+¯¯¯¯AC(1+B) 反向分配律
=AB+¯¯¯¯AC A+1=1
结论:¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A¯¯¯¯B+¯¯¯¯¯¯¯¯AC=AB+¯¯¯¯AC
4、!((x<=0||x>5)&&(y<=0||y>10)
设X=(x<=0),Y=(x>5),A=(y=0),B=(y>10)
原式=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(X+Y)(A+B)
=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯X+Y+¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A+B 摩根定律
=¯¯¯¯¯X⋅¯¯¯¯Y+¯¯¯¯A⋅¯¯¯¯B 摩根定律
也就是x>0&&x<=5||y>0&&y<=10



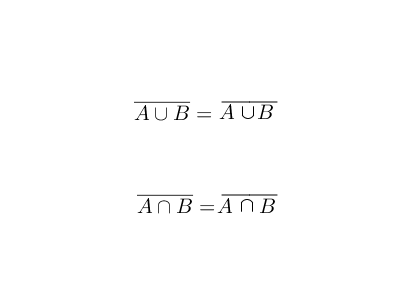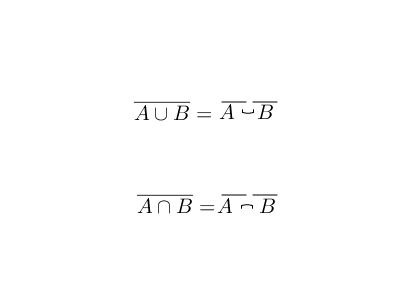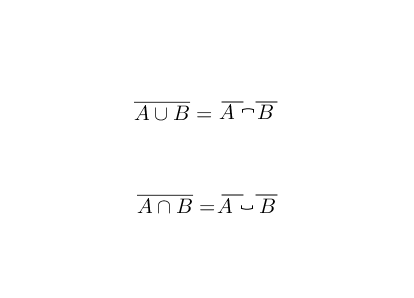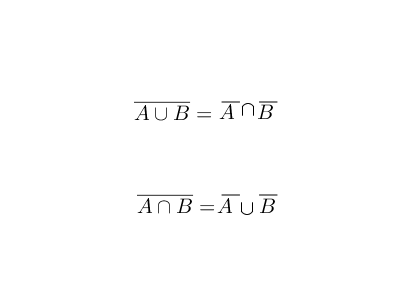




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2019-08-17 基于JFinal中搭建wopi协议支撑办法
2014-08-17 转发给吴斌