P1955 [NOI2015] 程序自动分析题解
一、惯性思维
我是刚刚做完上一题P1892团伙 后来做这一道题，粗略一看，相等，不相等，这不就是朋友的朋友，敌人的敌人吗？小意思！种类并查集模板走起！！！
但一看题解，才发现了自己的浅薄：
不等号不具备传递性，而等号具有传递性。\(a≠b\)和\(b≠c\)不能推出\(a≠c\)
这和朋友的朋友是朋友，敌人的敌人是朋友完全是两回事！！行不通
比如举出的反例 ：
1
3
1 2 0
2 3 0
1 3 0
在我的方法的连接下，本应是三个互不相等的数却出现了冲突
而正确的做法正是利用了不等号不具备传递性，我们将所有等号操作率先合并完了以后，再判断所有不等号是否成立，及两数是否在同一集合中，就可已完成此题
二、并查集版本
并查集的思路已经很明显了:首先把“相等”的条件搞好，也就是用并查集并起来。之后遍历所有“不等”的条件，只要有一对在同一个集合里，就不可能满足。
（1）如果说两个数字相等，那么就合并为同一家族。
（2）如果说两个数字不等，就检查以前它们是不是同一家族的，如果是，就是说明出现了矛盾，直接输入NO,退出即可。
但现实很残酷，一道绿题哪能是这么容易过的，第二个测试点RE：
#include <bits/stdc++.h>
using namespace std;
int t;//表示需要判定的问题个数
int n;//表示该问题中需要被满足的约束条件个数
int x; //第一个数
int y; //第二个数
int e; //是否相等，1相等，0不相等
const int N = 1e6 + 10;
int fa[N];
//先记录，再离散化
struct Node {
int x, y, e;
} a[N];
//先处理相等，再处理不相等的,这个排序器是用来决定相等优先的
bool cmp(const Node &a, const Node &b) {
return a.e > b.e;
}
//要深入理解这个递归并压缩的过程
int find(int x) {
if (fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
}
//加入家族集合中
void join(int c1, int c2) {
int f1 = find(c1), f2 = find(c2);
if (f1 != f2)fa[f1] = f2;
}
int main() {
cin >> t;
while (t--) {
cin >> n;
//初始化,因为有多个问题，每个问题问之前，都需要清理下场地
memset(a, 0, sizeof a);
memset(fa, 0, sizeof fa);
//录入
for (int i = 1; i <= n; i++)
cin >> a[i].x >> a[i].y >> a[i].e;
//排序，先处理相等的，再处理不相等的.这样才能保证亲戚都认领完了，再找出矛盾。
sort(a + 1, a + 1 + n, cmp);
//初始化并查集
for (int i = 1; i < N; i++) fa[i] = i;
bool success = true;
for (int i = 1; i <= n; i++) {
if (a[i].e == 1) join(a[i].x, a[i].y);
else {
int f1 = find(a[i].x), f2 = find(a[i].y);
if (f1 == f2) {
success = false;
break;
}
}
}
if (success) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}
上面的代码也不错啊，可以获得大部分本题的得分。有一个核心的问题：就是排序。
为什么要排序呢？
因为并查集是一个家族关系的维护问题，我们的思路是创建家族关系，再找出不是一个家族关系的矛盾问题。
三、离散化+并查集版本
为什么会出现上面的情况呢？其实我们忽略了一个最基本的常知：OI中，必须关注数据范围~~
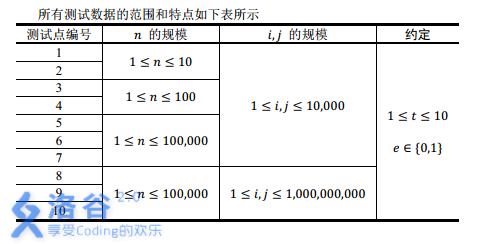
看到了没，这\(i,j\)都是上限\(1e9\)啊，我们开的数组\(fa[N]\)，它能表示的范围是\(1e6+10\),太小了，不死才怪！
那我们把\(N\)扩大到 \(1e9+10\)是不是就可以了呢？？
当然不行了，要不还能叫绿题！！NOIP中，有如下的规则上限：
空间上限128MB
\(int = 4\)字节
\(char = 1\)字节
\(long long = 8\)字节
\(128M = 128 *1024k= 131072KB = 134217728\)字节
$int$型一维数组最多是3千万
$long\ long$型一维数组最多是1千5百万
$char$型一维数组最多是1亿左右
C++完整代码
#include <bits/stdc++.h>
using namespace std;
//此题，数据范围太大，必须离散化处理（这是策略二，还需要一种简单版本的离散化）
//关注一下数据范围，是有10的9次方那么大，如果开一个10的9次方大的fa数组的话，空间肯定超限，超限就凉凉
int t;//表示需要判定的问题个数
int n;//表示该问题中需要被满足的约束条件个数
int x; //第一个数
int y; //第二个数
int e; //是否相等，1相等，0不相等
const int N = 1000010;
int fa[N];
//要深入理解这个递归并压缩的过程
int find(int x) {
if (fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
}
//加入家族集合中
void join(int c1, int c2) {
int f1 = find(c1), f2 = find(c2);
if (f1 != f2)fa[f1] = f2;
}
//先记录，再离散化
struct Node {
int x, y, e;
} a[N];
//先处理相等，再处理不相等的,这个排序器是用来决定相等优先的
bool cmp(const Node &a, const Node &b) {
return a.e > b.e;
}
int main() {
cin >> t;
while (t--) {
cin >> n;
//初始化
memset(a, 0, sizeof a);
memset(fa, 0, sizeof fa);
//录入+离散化
vector<int> alls; // 存储所有待离散化的值
for (int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y >> a[i].e;
alls.push_back(a[i].x), alls.push_back(a[i].y);
}
// 将所有值排序
sort(alls.begin(), alls.end());
// 去掉重复元素
alls.erase(unique(alls.begin(), alls.end()), alls.end());
// 二分求出x对应的离散化的值
for (int i = 1; i <= n; i++) {
a[i].x = lower_bound(alls.begin(), alls.end(), a[i].x) - alls.begin();
a[i].y = lower_bound(alls.begin(), alls.end(), a[i].y) - alls.begin();
}
//排序，先处理相等的，再处理不相等的.这样才能保证亲戚都认领完了，再找出矛盾。
sort(a + 1, a + 1 + n, cmp);
//初始化并查集
for (int i = 1; i <= alls.size(); i++) fa[i] = i;
bool success = true;
for (int i = 1; i <= n; i++) {
if (a[i].e == 1) join(a[i].x, a[i].y);
else {
int f1 = find(a[i].x), f2 = find(a[i].y);
if (f1 == f2) {
success = false;
break;
}
}
}
if (success) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}
四、数据很水，MOD也一样过
这道题的出题人太良心了，数据很水，没有故意制造冲突数据。通过下面简单取模的办法，就可以把此题AC掉。但这不是正确的方法，还是推荐上面闫老师的离散化大法~，那个才是王道，下面的解法出问题的概率很高。
#include <bits/stdc++.h>
using namespace std;
//此题，数据范围太大，必须离散化处理（这是策略一，简单版本的离散化）
//关注一下数据范围，是有10的9次方那么大，如果开一个10的9次方大的fa数组的话，空间肯定超限，超限就凉凉
int t;//表示需要判定的问题个数
int n;//表示该问题中需要被满足的约束条件个数
int x; //第一个数
int y; //第二个数
int e; //是否相等，1相等，0不相等
const int N = 1000005;
const int MOD = 1000003; //从这值是从P1955_Prepare.cpp中计算到的
int fa[N];
//要深入理解这个递归并压缩的过程
int find(int x) {
if (fa[x] != x) fa[x] = find(fa[x]);
return fa[x];
}
//加入家族集合中
void join(int c1, int c2) {
int f1 = find(c1), f2 = find(c2);
if (f1 != f2)fa[f1] = f2;
}
//先记录，再离散化
struct Node {
int x, y, e;
} a[N];
//先处理相等，再处理不相等的,这个排序器是用来决定相等优先的
bool cmp(const Node &a, const Node &b) {
return a.e > b.e;
}
int main() {
cin >> t; //需要判断问题的个数
while (t--) {//多个问题
cin >> n;
//初始化,因为有多个问题，每个问题问之前，都需要清理下场地
memset(a, 0, sizeof a);
memset(fa, 0, sizeof fa);
//录入+离散化
for (int i = 1; i <= n; i++) {
int x, y;
cin >> x >> y >> a[i].e;
a[i].x = x % MOD, a[i].y = y % MOD;
}
//排序，先处理相等的，再处理不相等的.这样才能保证亲戚都认领完了，再找出矛盾。
sort(a + 1, a + 1 + n, cmp);
//初始化并查集
for (int i = 1; i <= N; i++) fa[i] = i;
bool success = true;
for (int i = 1; i <= n; i++) {
if (a[i].e == 1) join(a[i].x, a[i].y);
else {
int f1 = find(a[i].x), f2 = find(a[i].y);
if (f1 == f2) {
success = false;
break;
}
}
}
if (success) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}
找出一个合适的质数：
#include <bits/stdc++.h>
using namespace std;
const int N = 10000810;
int primes[N], cnt;
bool st[N];
void get_primes(int n) {
for (int i = 2; i <= n; i++) {
if (!st[i]) primes[cnt++] = i; //没有被标识过，就增加到质数数组中去
// 线性筛法核心:N 只会被它最小的质因子筛掉
// 从小到大枚举所有可能满足条件的质数
for (int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true; //从小向大，所以这里可以这么写primes[j],标识st[primes[j] * i]已经标识过了
//最小质因子就可以了，其它质因子放弃掉，看上面的链接里有原因说明
if (i % primes[j] == 0) break;
}
}
}
int main() {
get_primes( 1e6 + 10);
for (int i = 0; i < cnt; i++) cout << primes[i] << " ";
return 0;
}
