P1525 [NOIP2010 提高组] 关押罪犯

题目传送门

一、种类并查集模板题

学习网站：https://zhuanlan.zhihu.com/p/97813717

一般的并查集，维护的是具有连通性、传递性的关系，例如亲戚的亲戚是亲戚。但是，有时候，我们要维护另一种关系：敌人的敌人是朋友。种类并查集就是为了解决这个问题而诞生的。

其实很容易想到，本题可以贪心，把所有矛盾关系从大到小排个序，然后尽可能地把矛盾大的犯人关到不同的监狱里，直到不能这么做为止。这看上去可以用并查集维护，但是有一个问题：我们得到的信息，不是哪些人应该在相同的监狱，而是哪些人应该在不同的监狱。这怎么处理呢？这个题其实有很多做法，但这里，我们介绍使用种类并查集的做法。

我们开一个两倍大小的并查集。例如，假如我们要维护4个元素的并查集，我们改为开8个单位的空间：

我们用\(1 \sim 4\)维护朋友关系（就这道题而言，是指关在同一个监狱的狱友），用\(5 \sim 8\)维护敌人关系（这道题里是指关在不同监狱的仇人）。现在假如我们得到信息：\(1\)和\(2\)是敌人，应该怎么办？

我们\(join(1, 2+n), join(1+n, 2)\);。这里\(n\)就等于\(4\)，但我写成\(n\)这样更清晰。对于1个编号为\(i\)的元素，\(i+n\)是它的敌人。所以这里的意思就是：\(1\)是\(2\)的敌人，\(2\)是\(1\)的敌人。

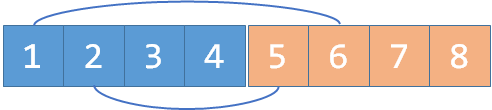
现在假如我们又知道\(2\)和\(4\)是敌人，我们\(join(2, 4+n), join(2+n, 4)\)：

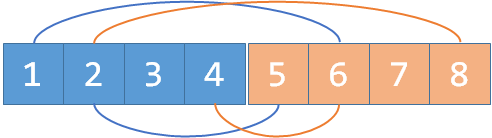
发现了吗，敌人的敌人就是朋友，\(2\)和\(4\)是敌人，\(2\)和\(1\)也是敌人，所以这里，\(1\)和\(4\)通过\(2+n\)这个元素间接地连接起来了。这就是种类并查集工作的原理。

二、相关例题

http://poj.org/problem?id=2492

三、C++代码

#include <bits/stdc++.h>

using namespace std;
const int N = 20010;
const int M = 100010;

int n, m, x, y;

//fa[i]表示i所属的集合，用fa[i+n]表示i所属集合的补集，实现的很巧妙，可以当成一个使用并查集的巧妙应用；
int fa[N << 1];  //并查集数组,有时也写成 N << 1 ,从左到右，读作N左移1位，就是 2*N

//要深入理解这个递归并压缩的过程
int find(int x) {
    if (fa[x] != x) fa[x] = find(fa[x]);
    return fa[x];
}

//加入家族集合中
void join(int c1, int c2) {
    int f1 = find(c1), f2 = find(c2);
    if (f1 != f2)fa[f1] = f2;
}

//关系
struct node {
    int x; //第一个人
    int y; //第二个人
    int v; //冲突值
} a[M];

//排序函数，按冲突值大小排序，大的在前
bool cmp(const node &a, const node &b) {
    return a.v > b.v;
}

int main() {
    //读入
    cin >> n >> m;
    for (int i = 1; i <= m; i++) cin >> a[i].x >> a[i].y >> a[i].v;
    //排序
    sort(a + 1, a + m + 1, cmp);

    //初始化并查集，每个人都是自己的祖先
    for (int i = 1; i <= 2 * n; i++)fa[i] = i;//注意这里是2*n

    //处理m组关系
    for (int i = 1; i <= m; i++) {
        x = find(a[i].x);
        y = find(a[i].y);
        if (x == y) {
            cout << a[i].v << endl;
            return 0;
        } else
            join(a[i].y + n, x), join(a[i].x + n, y);
    }
    cout << 0 << endl;
    return 0;
}