AcWing 785. 快速排序
. 快速排序
一、题目描述
给定你一个长度为 的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数 。
第二行包含 个整数(所有整数均在 范围内),表示整个数列。
输出格式
输出共一行,包含 个整数,表示排好序的数列。
数据范围
输入样例:
5
3 1 2 4 5
输出样例:
1 2 3 4 5
二、算法原理
-
每次排序时选取一个基准,将小于基准的数全部放到基准点的左边,将大于或等于基准的数全部放到基准的右边。
-
完成后,得到了两个 整体 上有序的子数组,再递归继续,直至所有元素完成排序。
算法模拟
假设对这个数进行排序:
本次模拟的基准是以数组的第一个元素为基准的。
从后向前扫描,去向右找第一个大于 基准 (这个是选择的第一元素,代码中我们将选择中间位置的元素,道理都是一样的) 的数字,向左查找第一个小于基准数字:
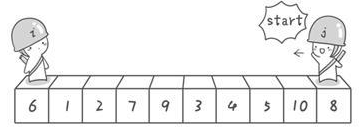
找到和,交换和
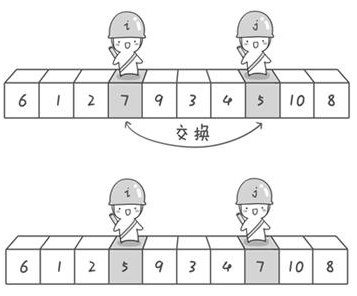
继续前进,找到和,然后交换

,交换和
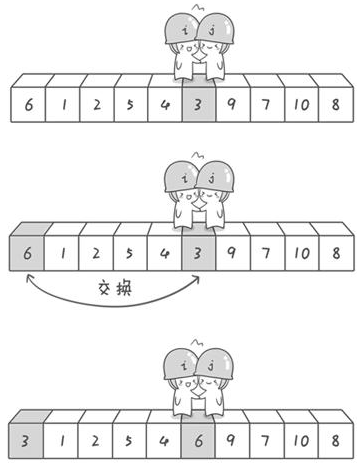
交换之后:, 一趟排序结束。
以基准值划分的两堆数据,左手边都比小,右手边都比大,在中间,然后再用同样的办法递归处理左右两边即可,此时,就不参与了。
三、实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int q[N];
int n;
/**
* 功能:利用快速排序对数组进行排序
* @param q 要排序的数组
* @param l 左端下标位置
* @param r 右端下标位置
*/
void quick_sort(int q[], int l, int r) {
if (l >= r) return;
int i = l - 1, j = r + 1; // 从界外开始
int x = q[(l + r) >> 1]; // 基准值为中间位置的数值
while (i < j) { // 没有碰面就一直按这个逻辑跑一跑
do i++;
while (q[i] < x); // i哨兵向右走,找到第一个大于基准值的数,这个数的位置需要调整
do j--;
while (q[j] > x); // j哨兵向左走,找到第一个小于基准值的数,这个数的位置需要调整
if (i < j) swap(q[i], q[j]); // 如果还没有碰面,就对调一下
}
// 当退出上面的循环,就是两个人碰面的时候,此时左右两半都已经是有序的了,再递归处理
quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> q[i];
quick_sort(q, 1, n);
for (int i = 1; i <= n; i++) printf("%d ", q[i]);
return 0;
}
四、快速排序算法的证明与边界分析 【了解】

琢磨太深,使人痛苦!
顺带一提用做划分时的模板
void quick_sort(int q[], int l, int r) {
if (l >= r) return;
int i = l - 1, j = r + 1;
int x = q[(l + r + 1) >> 1]; // 非得要用i这里要修改!
while (i < j) {
do i++;
while (q[i] < x);
do j--;
while (q[j] > x);
if (i < j) swap(q[i], q[j]);
}
quick_sort(q, l, i - 1), quick_sort(q, i, r); // 非得要用i这里要修改!
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2019-07-12 处理天桥无法访问故障一例
2019-07-12 解决 SSH Connection closed by foreign host 问题
2018-07-12 icomet研究