P4924 [1007]魔法少女小Scarlet 题解
解题思路:
看到数据范围后知道这道题是道模拟,然后我们又发现数据的范围保证不会出现越界的情况(良心啊qwq),所以我们不需要特别判断是否越界。然而我比较菜,推了大半天式子还错了。。 因为矩阵是绕着某个中心\((x,y)\)旋转的而且保证是正方形,为了得到正确的式子、便于理解,我们不妨设\((x,y)\)为原点\((0,0)\),这样稍微模拟一下就可以得到顺时针旋转90°后正方形上一点\((i,j)\)坐标变成\((j,-i)\),逆时针旋转90°后坐标变成\((-j,i)\),然后枚举\(i,j\)即可。
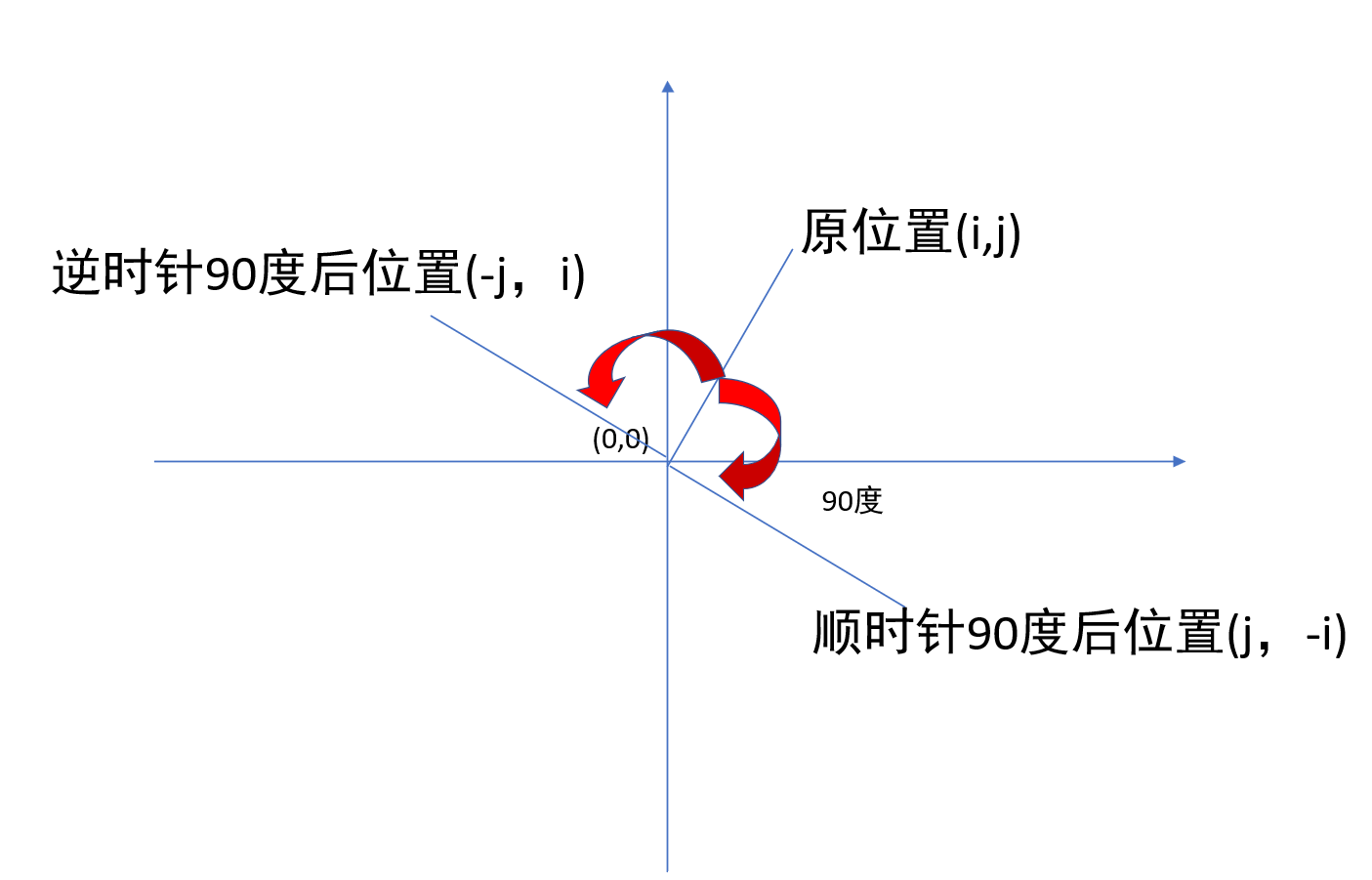
注意:
这里可能有的同学不理解,我们明明在是数组上操作,数组上操作是没有负号的,你上面怎么用直角坐标系来推导?那个负号怎么办啊?
其实,在数组中,我们并不是从\((0,0)\)这个点为中心的,而是以\((x,y)\)为中心,就是每个推导的结果在横坐标和纵坐标上要分别加上\(x,y\)就是可解决到负号的问题,这个也就是坐标平移的意思了。
再深层的含义,可能需要纸和笔按样例使用推出来的公式验证一下就明白了。> 很简单的(开玩笑,很简单???)

下面的准备的知识点,先试一下吧:
1、二维数组顺时针旋转90度
#include <bits/stdc++.h>
using namespace std;
// Rotate Image(二维数组顺时针旋转90度)
const int N = 110;
int n = 9, cnt;
int res[N][N], tmp[N][N];
//矩阵旋转,需要额外开创建一个临时的二维数组(防止出现交换赋值时,出现覆盖的问题)
void rotate(int x, int y, int r) {
for (int i = -r; i <= r; i++)
for (int j = -r; j <= r; j++)
//每一个位置都去了哪里
tmp[x + j][y - i] = res[x + i][y + j];
//复制回来
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res[i][j] = tmp[i][j];
}
int main() {
//初始化数据
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res[i][j] = tmp[i][j] = ++cnt;
//输出结果
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
printf("%2d ", res[i][j]);
printf("\n");
}
printf("\n");
//测试一下旋转
rotate(6, 7, 1);
//输出结果
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
printf("%2d ", res[i][j]);
printf("\n");
}
return 0;
}
2、二维数组逆时针旋转90度
#include <bits/stdc++.h>
using namespace std;
// Rotate Image(二维数组逆时针旋转90度)
const int N = 110;
int n = 9, cnt;
int res[N][N], tmp[N][N];
//矩阵旋转,需要额外开创建一个临时的二维数组(防止出现交换赋值时,出现覆盖的问题)
void rotate(int x, int y, int r) {
for (int i = -r; i <= r; i++)
for (int j = -r; j <= r; j++)
tmp[x - j][y + i] = res[x + i][y + j];
//复制回来
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res[i][j] = tmp[i][j];
}
int main() {
//初始化数据
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res[i][j] = tmp[i][j] = ++cnt;
//输出结果
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
printf("%02d ", res[i][j]);
printf("\n");
}
printf("\n");
//测试一下旋转
rotate(6, 7, 1);
//输出结果
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++)
printf("%02d ", res[i][j]);
printf("\n");
}
return 0;
}
3、本题解答
#include<bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m;
int x, y, r, z;
int tmp[N][N], res[N][N];
int cnt;
// 数组res为最后输出的结果数组,tmp为辅助数组;
int main() {
cin >> n >> m;
//初始化数据
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res[i][j] = tmp[i][j] = ++cnt;
//读入魔法指令
while (m--) {//m次指令
cin >> x >> y >> r >> z;
//处理旋转
if (z == 0) { //顺时针
for (int i = -r; i <= r; i++) //i为以(x,y)为中点的偏移量,可以用来描述横坐标
for (int j = -r; j <= r; j++)//j为以(x,y)为中点的偏移量,可以用来描述纵坐标
//防止自己覆盖掉自己,在副本上操作
//遍历每一个范围内的坐标,根据上图,确定最终的坐标
res[x + j][y - i] = tmp[x + i][y + j];
} else if (z == 1) {//逆时针
for (int i = -r; i <= r; i++)
for (int j = -r; j <= r; j++)
//防止自己覆盖掉自己,在副本上操作
//遍历每一个范围内的坐标,根据上图,确定最终的坐标
res[x - j][y + i] = tmp[x + i][y + j];
}
//更新辅助数组
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
tmp[i][j] = res[i][j];
}
//输出
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) cout << res[i][j] << ' ';
cout << endl;
}
return 0;
}

