NOIP2018普及初赛解析

2018年第二十四届全国青少年信息学奥林匹克联赛初赛普及组真题解析

一、单项选择题

1. 以下哪一种设备属于输出设备：（D）

A.扫描仪 _B.键盘C. 鼠标 _D. 打印机

解析：送分题，前三个都是输入设备

 

2. 下列四个不同进制的数中，与其它三项数值上不相等的是（D）。

A.(269)16

B.(617)10

C.(1151)8

D.(1001101011)2

解析：

1)方法一：是把4个都换成10进制来比较。

2)方法二：直接通过二进制转八、十六进制的快速转换方法来判断。

二进制转八进制是3个并1个、转十六进制是4个并1个。

对D的二进制数分析：

(1001 101 011)2 = (1153)8

(100110 1011)2 = (26B)16

显然，与其它不符的只能是D

解析：有点难度，有点意思

 

3. 1MB 等于（D）。

A. 1000字节 B. 1024字节

C. 1000 X 1000字节 D. 1024 X1024字节

解析：2015年相同的题

1MB＝1024KB， 1KB＝1024字节

 

4. 广域网的英文缩写是（B）。

A.LAN

B.WAN

C.MAN

D.LNA

解析：

WAN:Wide area network

 

5. 中国计算机学会于（B）年创办全国青少年计算机程序设计竞赛。

A.1983

B.1984

C.1985

D.1986

解析：

1984年，*说计算机的普及要从娃娃抓起，那一年的中国科协和计算机协会一起举办了全国青少年程序设计大赛

这个，只能靠记忆了，没办法。

 

6. 如果开始时计算机处于小写输入状态，现在有一只小老鼠反复按照CapsLock、字母键A、字母键S、字母键D、字母键F的顺序循环按键，即CapsLock、A、S、D、F、CapsLock、A、S、D、F、……，屏幕上输出的第81 个字符是字母（A）。

A. A

B. S

C. D

D. a

解析：有坑有坑，小心别掉坑！！

2016年的雷同题,本题思路如下：、

方法一：

CapsLock为大小写切换（没有输出），所以默认按键5个（输出4个）为一轮。

81 ＝ 4*20 ＋ 1，即从0轮开始，求第20轮的第一个输出。

开始状态为小写，第0轮为大写，第1轮为小写，依次类推，第20轮为大写。

所以答案为大写状态的第一个字符‘A’

方法二：以8个输出为一轮，每轮都重复输出，则81个字符与第1个字符相同。

7. 根节点深度为0，一棵深度为h 的满k（k>1）叉树，即除最后一层无任何子节点外，每一层上的所有结点都有k 个子结点的树，共有（A）个结点。

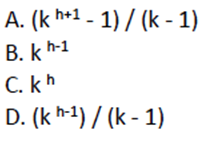
解析：
1）假设h=2，k=2，画出完美二叉树，共7个节点。
2）对4个答案代入运算，结果为A
如果想理解和推导公式：

 

8. 以下排序算法中，不需要进行关键字比较操作的算法是（A）。

A.基数排序

B.冒泡排序

C.堆排序

D.直接插入排序

解析：
  • 基数排序用桶数组来存储，利用桶数组的下标直接实现了排序，无需比较。
  • 后三个都要比较。

9. 给定一个含N 个不相同数字的数组，在最坏情况下，找出其中最大或最小的数，至少需要N - 1 次比较操作。则最坏情况下，在该数组中同时找最大与最小的数至少需要（A）次比较操作。（⌈ _⌉表示向上取整，⌊ _⌋表示向下取整）

A.⌈ 3N-2⌉-2

B.⌊3N-2⌋-2

C.2N-2

D.2N-4

解析：
  • 如果分别找最大值、最小值，则至少都需要N-1次操作。
  • 同时找最大最小值，有更优化的方法，如果没有学过这个算法，本题只能根据题面猜测肯定小于2N-2，需在A和B里面蒙一个，50%几率。
  • 学过的话，按照下面的优化算法：
  • N为奇数时，比较次数为3*(N-1)/2 =(3N+1)/2 - 2
  • N为偶数时，比较次数为1 +3*(N-2)/2 = 3N/2 – 2
  • 综合奇偶，显然答案为A
找最大最小值的优化算法：
  • 初始值：
  • N为奇数，最大值、最小值的初始值都设为第一个元素。
  • N为偶数，将前两个元素比较，最大值初始值为大的元素，最小值初始值为小的元素。
  • 枚举，每次两个元素（循环步长为2）
  • 比较两个元素，分出大小。
  • 大的元素与最大值比较，比最大值大则设为该元素。
  • 小的元素与最小值比较，比最小值小则设为该元素。
  • 循环结束，得到最大、最小值。

10. 下面的故事与（B）算法有着异曲同工之妙。

从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：“从前有座山，山里有座庙，庙里有个老和尚在给小和尚讲故事：‘从前有座山，山里有座庙，庙里有个老和尚给小和尚讲故事……’” _

A. 枚举

B. 递归

C. 贪心

D. 分治

解析：2013年相同的题。

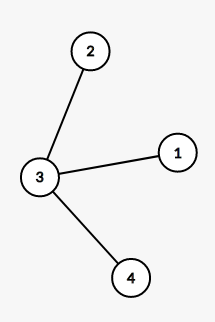
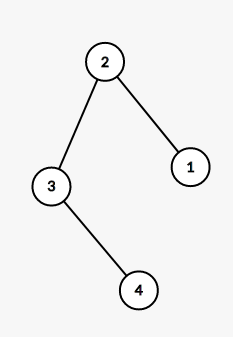
11. 由四个没有区别的点构成的简单无向连通图的个数是（A）。

A.6

B.7

C.8

D.9

解析：
1) 四个区别的点，意味着以下的图形为相同形状。

用d=[1, 2, 2,1]表示对应点的度，则以上的图的d数组都是一样的。

2）而以下的图形则是不同的另外一个形状，其d=[1, 3, 1, 1]。

题目要求，实际就是找出不同的d数组的个数。
3）根据边数来分类判断：
  1. 小于3条边，不构成连通，排除掉。
  2. 3条边：d=[1, 2, 2, 1]和[1, 3,1,1]两种
  3. 4条边：d=[2,2,2,2]和[1,3,2,2]两种
  4. 5条边：d=[2,2,3,3]一种
  5. 6条边：d=[3,3,3,3]一种
一共6种不同的图形，答案是A。

4）简单图指没有平行边和自环，不要被它误导。
更多：从6条边往下减边，会更加容易分析。

12. 设含有10 个元素的集合的全部子集数为S，其中由7个元素组成的子集数为T，则T / S 的值为（B）。

A.5 / 32

B.15 / 128

C.1 / 8

D.21 / 128

解析：
  1. 子集总数S为 2的10次方= 1024
  2. 7个元素集合数T为C（10,7）=10!/（3!7!）= 120
  3. T/S = 120/1024 = 15/128

13. 10000 以内，与10000 互质的正整数有（B）个。

A.2000

B.4000

C.6000

D.8000

解析：
互质的意思，与10000没有公约数，也即不能被10000的质因子整除。
  • 10000分解质因子：10000 =2*2*2*2*5*5*5*5
  • 10000以内被2整除的数有5000个
  • 10000以内被5整除的数有2000个
  • 2）和3）重复计算的数，即被10整除的数，有1000个。
  • 被2或5整除的数有：5000 +2000 – 1000 =6000
  • 互质的数有：10000 - 6000 ＝ 4000个

14. 为了统计一个非负整数的二进制形式中1 的个数，代码如下： _

intCountBit(int x)

{

intret = 0;

while(x)

{

ret++;

___________;

}

returnret;

}

则空格内要填入的语句是（ B）。 _

A.x >>= 1

B.x &= x - 1

C.x |= x >> 1

D.x <<= 1

解析：
  • 如果知道x = x&(x-1)是二进制从后往前去掉1个1的话，答案B自然知道。
  • 如果不知道的话，就自己模拟一下吧，比如用一个数5=(101)2
  • A选项模拟，结果为3
  • B选项模拟，结果为2
  • C选项模拟，死循环
  • D选项模拟，死循环

15. 下图中所使用的数据结构是（B）。

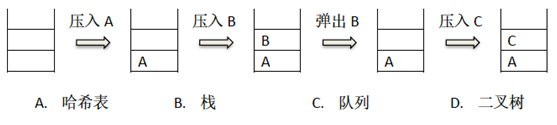
解析：
2013年相同的题。

今年难度大了很多，也有很多毒瘤题..

这篇博客尝试详尽地解析NOIP2018普及初赛.

题目

 

答案

先附上答案

 

单项选择题

1.C

送分题 其他都是输入设备

2.D

A: (269)16=617

B: 617

C: (1151)8=617

D: (1001101011)2=619

3.D

常识性知识

1GB=1024KB=1024∗1024B

4.A

广域网-Wide Area Network-WAN

想Wide就可以了

5.B

CCF赞歌，最近几乎每年都有。

直接拿今年年份减去届数（2018-24=1984）。

6.A

小学奥数。在历年的基础上改了下。每8个字母（ASDFasdf

）一个循环，81

，所以为A.

7.A

可以正经推出。但考试的时候如果不知道那可以画几个例子，然后带进去算。算出来A为正确。

注意本题树根深度记做0.

8.A

基数排序就是桶排序，所以不用比较。

没听说过？

B.冒泡和D.插入一定知道吧，都需要对比。C.堆排，堆的数据插入后上浮下沉操作需要比对，所以排除法选A。

9.A

看题目首先排除C和D。

然后时间复杂度一般要考虑最坏所以向上取整(然而我还是错了)。

10.B

送分。

11.C

分类讨论。

如下所示:

     

 

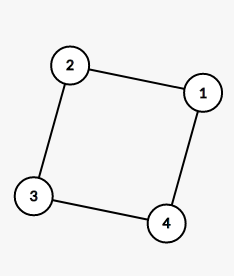
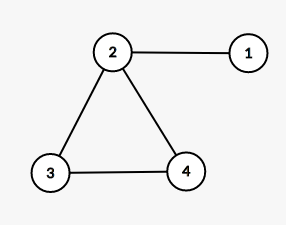
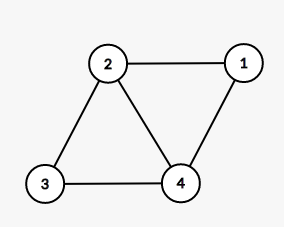
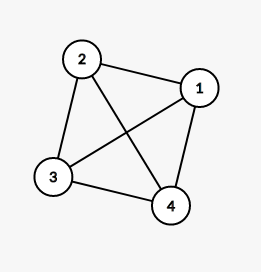
12.B

注意空集

13.B

小学奥数，分解质因数10000=24∗54

，2的倍数有4999个，5的倍数有1999个，除去10(2和5的公倍数)999个，加上10000这一个数，不互质的就是6000个，互质的就是10000-6000=4000个

14.B

状压DP常规操作，实在不行模拟也可。

15.B

不用多说，先进先出，栈。

问题求解

1

小学奥数，从③推出丁不去，又从④推出甲去了，然后由①推出没下雨。

2

分类讨论。

1-9中：1个

10-99中：1*8+10=18个

100-999中：(1+18)*8+100=252个

1000-1999中：1+18+252=271个

2000-2018中：2个

总共 1+18+252+271+2=544个

注意最后的2个要加上去，我是不会说我没加的。

阅读程序写结果

1

读题意就是将所有大写字母变成字母后一位，如'A'变成'B'，'E'变成'F'.

输出：RuanHuoMianTai

2

读题意得 0-15 每一个数的平方模15 是不是等于1

枚举和模的时候要细心

输出：4

3

做的时候暴力模拟，后来知道可以用表格。

f[i][j]=f[i−1][j]−f[i][j−1]+f[i−1][j−1]

表格长这样

 

n/m
0123456
0 0 1 2 3 4 5 6
1 1 0 3 2 5 4 7
2 2 -1 4 1 6 3 8
3 0 1 2 3 4 5 6
4 1 0 3 2 5 4 7
5 2 -1 4 1 6 3 8

输出：8

4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include <cstdio>
int n,d[100];
bool v[100];
int main(){
    scanf("%d",&n);
    for (int i=0;i<n;++i) {
        scanf("%d",d+i);
        v[i]=false;
    }
    int cnt=0;
    for (int i=0;i<n;++i) {
        if (!v[i]){
            for (int j=i;!v[j];j=d[j]) {
                v[j]=true;
            }
        ++cnt;
        }
    }
    printf("%d\n", cnt);
    return 0;
}

暴力模拟即可

输出：6

完善程序

1.最大公约数之和

(1)

i∗i

，枚举到n−−√

(2)

n/i

(3)

return a

(4)

a%b

(5)

gcd(a[i],a[j])+ans

2.双向链表求排列

(1)

a[x]=i

(2)

i+1

(3)

R[a[i]]，对称填

(4)

a[i]，刚开始对称填错了，双向链表操作

(5)

R[i]

posted @ 2019-03-30 07:39  糖豆爸爸  阅读(6309)  评论(1)  编辑  收藏  举报
Live2D