梯度下降
本文以线性回归为例,讲解了批量梯度下降、随机梯度下降、小批量梯度下降、冲量梯度下降等算法,由浅入深,并结合精心设计的例子,使读者最快掌握这种最常用的优化方法。每一种优化方法,笔者都基于R语言给出了相应的代码,供读者参考,
梯度下降
假如我们有以下身高和体重的数据,我们希望用身高来预测体重。如果你学过统计,那么很自然地就能想到建立一个线性回归模型:
其中\(a\)是截距,\(b\)是斜率,\(y\)是体重,\(x\)是身高。

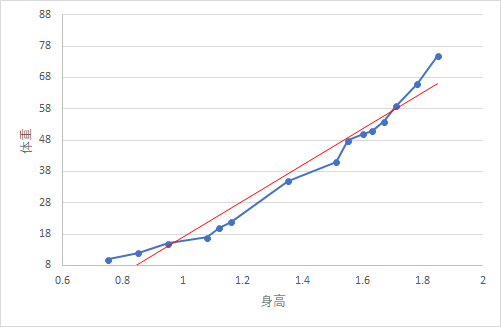
我们将身高与体重的关系在Excel里面用折线图表示,并且添加了线性的趋势线。蓝色的线条是真实数据,红色的实线是模型给出的预测值。蓝色线条与红色线条之间的距离绝对值是预测误差。所以,我们要找到最优的\(a\)和\(b\)来拟合这条直线,使得我们模型的总误差最小。
我们使用均方误差来表示模型的误差,由于\(Ypred = a + bx\),因此,模型的均方误差可以表示为
也就是说,\(SSE\)是关于\(a\)和\(b\)的函数,我们只需要不断调整\(a\)和\(b\),使\(SSE\)降到最低就可以了。这个时候,我们就可以利用梯度下降算法,来求解\(a\)和\(b\)的值。
梯度下降的计算过程如下:
step 1:随机初始化权重\(a\)和\(b\),计算出误差\(SSE\)
step 2:计算梯度。 \(a\)和\(b\)的轻微变化都会导致\(SSE\)的变化,因此,我们只需要找到能使\(SSE\)减小的\(a\)和\(b\)的变化方向就可以了。这个方向,一般就是由梯度决定的。
step 3:调整权重值,使得\(SSE\)不断接近最小值。
step 4:使用新的权重去做预测,并且计算出新的\(SSE\)。
step 5:重复step2-step3,直到权重不再显著变化为止。

我们在Excel中进行上述步骤。为了计算能够快一点,我们首先对数据进行Min-Max标准化。得到如下数据:

step1:随机选取一组权重(此处我们设置a=0,b=1),我们计算出预测值和误差:
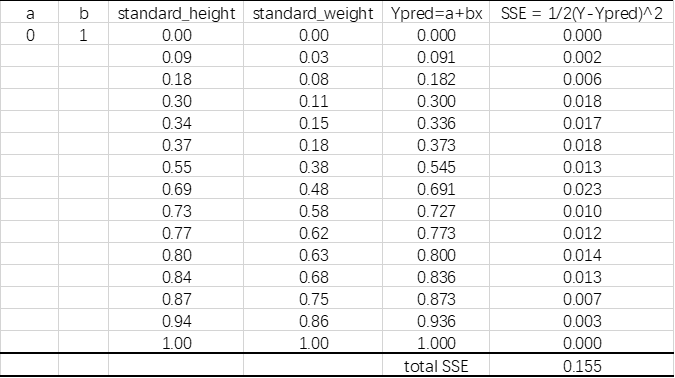
step2:计算梯度
\(\frac{\partial SSE}{\partial a}\)和\(\frac{\partial SSE}{\partial b}\)就是梯度,他们决定了\(a\)和\(b\)的移动方向和距离。
step3: 调整权重值,使得\(SSE\)不断接近最小值。
调整规则为:
其中,\(\eta\)是一个被我们称之为学习率(learning rate)的东西,一般设置为0.01或者你希望的任何比较小的数值。
本文选择0.01作为学习率。
step4:使用新的权重去做预测,并且计算出新的\(SSE\)。
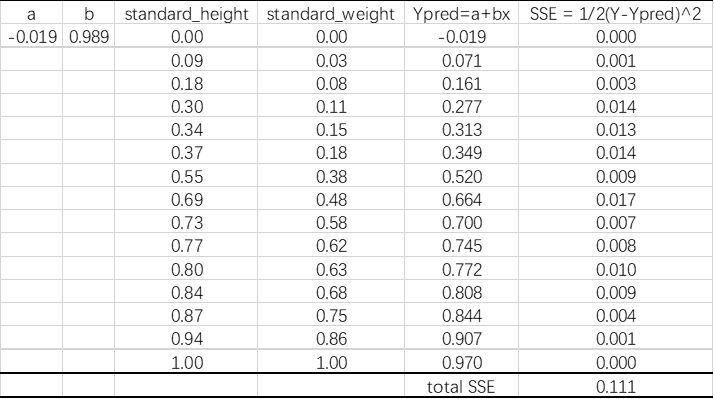
可以看出,SSE从0.155降低到0.111,说明系数有改善。
step 5:重复step2-step3,直到权重不再显著变化为止。
我们知道,一元线性回归的系数可以用公式计算,我们用R的lm()函数来计算权重,结果为
lm(y~x,dat)
Call:
lm(formula = y ~ x, data = dat)
Coefficients:
(Intercept) x
-0.1167 0.9777
然后,我在R里面写了一个梯度下降的函数,当精度调到0.0000001的时候,与lm的结果已经很接近了。
gradientDescent <- function(dat,start = c(0,0),learning_rate = 0.01,tol = 0.001)
{
a = start[1]
b = start[2]
x = dat[,1]
y = dat[,2]
iters = 0
while(TRUE)
{
Ypred = a + b * x
old_a = a
old_b = b
a = a + learning_rate * sum(y - Ypred)
b = b + learning_rate * sum((y-Ypred) * x)
iters = iters + 1
if(abs(a-old_a) <= tol & abs(b-old_b) <= 0.01)
break;
}
list(weights = c(a,b),iters = iters)
}
gradientDescent(dat,tol=0.0000001)
$weights
[1] -0.1167315 0.9776839
$iters #迭代了975次
[1] 975
我们常说的梯度,其实是指向量,其方向与切线方向相同。
利用梯度下降法进行权重更新的公式为:
\[weight_{new} = weight_{old} - \eta \cdot \nabla \]其中,那个倒三角形就是梯度的意思。我们在高中数学学过,切线方向是函数变化速度最快的方向,
Stochastic Gradient Descent
梯度下降算法,又可以称为Batch-Gradient-Gescent,即批量梯度下降算法。从上面的例子可以看出,批量梯度下降算法,每次更新系数都需要所有的样本参与计算,当样本规模达到一定数量以后,这个更新速度会非常慢。另外,还有可能导致内存溢出。
为了克服批量梯度下降的这个缺点,有人提出了随机梯度下降(Stochastic Gradient Descent)算法,即每次更新系数只需要一个样本参与计算,因此既可以减少迭代次数,节省计算时间,又可以防止内存溢出。
对于上述问题,随机梯度下降的算法过程如下:
for every \(Y_i\):
\(Ypred = a + bx\)
\(a = a + \eta (Y-Ypred)\)
\(b = b+\eta(Y-Ypred)\cdot x\)
随机梯度下降算法适用于大数量的计算,对于小数据量不一定准确。为了检验随机梯度下降算法,我们构造了一个有10000个样本的数据,同样是计算一元线性回归的系数。
随机梯度下降的函数如下:
stochasticGradientDescent <- function(dat,start = c(0,0),learning_rate = 0.01,tol = 0.000001,iteratons = 100)
{
#start:初始参数
#learning_rate:学习率
#tol:精度
#iterations:迭代次数
dat = as.matrix(dat)
a = start[1]
b = start[2]
x = dat[,1]
y = dat[,2]
iters = 0
while(iters < iteratons)
{
#重排,即将样本的顺序打乱
index = sample(length(x))
old_a = a
old_b = b
for(i in index)
{
Ypred = a + b * x[i]
a = a + learning_rate * (y[i] - Ypred)
b = b + learning_rate * (y[i]-Ypred) * x[i]
}
if(abs(a-old_a) <= tol & abs(b-old_b) <= tol)
break;
learning_rate = learning_rate / (1 + 0.01 * iters) #自适应学习率
iters = iters + 1
if(iters > iterations)
break;
}
list(weights = c(a,b),iters = iters)
}
然后我们构造一个相对大的样本用来检验算法:
set.seed(100)
x <- seq(1,10,length.out = 10000)
y <- 2 * x + rnorm(10000) * 10 + 2
bigdata <- data.frame(x ,y )
plot(x,y)
cor(x,y)
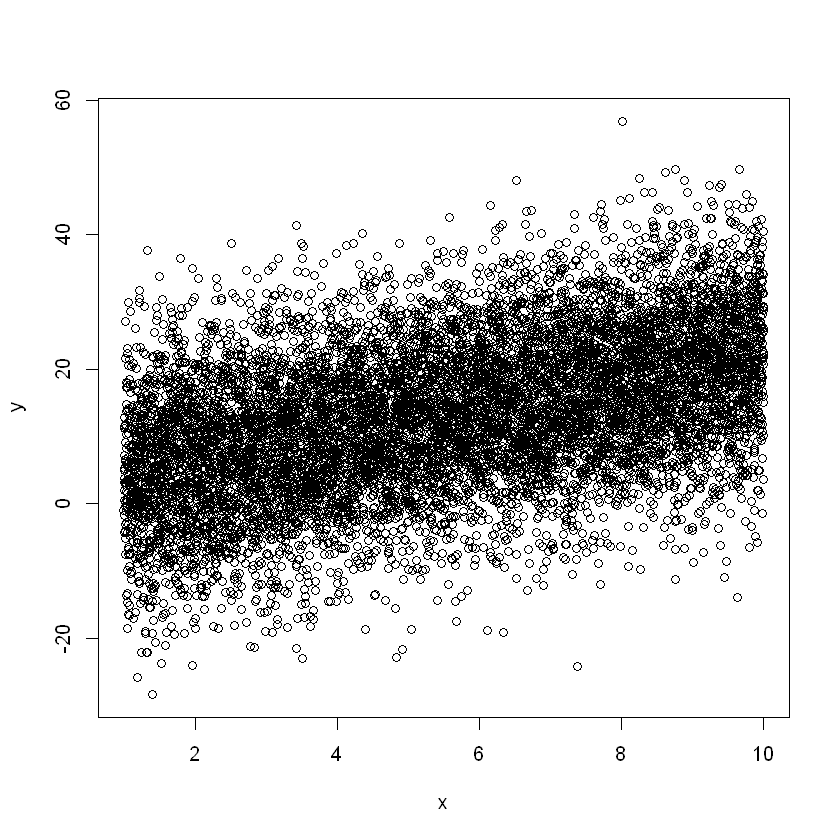
回归结果:
lm(y~x,data = bigdata )
Call:
lm(formula = y ~ x, data = bigdata)
Coefficients:
(Intercept) x
2.004 2.006
随机梯度下降的结果:
stochasticGradientDescent(bigdata,learning_rate = 0.001,tol=0.000000001)
$weights
2.01138749995603 2.00584502615877
$iters
69
批量梯度下降的结果:
batchGradientDescent(bigdata,learning_rate = 0.000001,tol = 0.000000001)
$weights
2.00385275101478 2.00634924457312
$iters
8345
可以看到,在同样的精度要求下,随机梯度下降进行59次迭代以后即收敛,而批量梯度下降则需要迭代8345次。
但是随机梯度下降也有一个缺点,即参数更新频率太快,有可能出现目标函数值在最优质附近的震荡现象,因为高频率的参数更新导致了高方差。 同时也可以看出,在相同精度要求下,随机梯度下降计算出来的系数与精确值离差较大,而批量随机下降则更接近精确值。
Mini-batch Gradient Descent
小批量梯度下降(Mini-batch Gradient Descent)是介于上述两种方法之间的优化方法,即在更新参数时,只使用一部分样本(一般256以下)来更新参数,这样既可以保证训练过程更稳定,又可以利用批量训练方法中的矩阵计算的优势。
具体更新哪些样本,通常是随机确定的,下面,我们定义一下小批量梯度下降的函数,用来求解上述bigdata的系数。
miniBatchGradientDescent <- function(dat,start = c(0,0),learning_rate = 0.01,tol = 0.001,batchSize = 256,iterations = 10000)
{
a = start[1]
b = start[2]
iters = 0
len = length(y)
while(TRUE)
{
mini_index = sample(len,batchSize,replace = FALSE)
x = dat[mini_index,1]
y = dat[mini_index,2]
Ypred = a + b * x
error = y - Ypred
old_a = a
old_b = b
a = a + learning_rate * sum(error)
b = b + learning_rate * sum((error) * x)
start = rbind(start,c(a,b))
iters = iters + 1
if(abs(a-old_a) <= tol & abs(b-old_b) <= tol)
break
if(iters >= iterations)
break
}
list(weights = c(a,b),iters = iters,coes = start)
}
miniBatchGradientDescent(bigdata,learning_rate = 0.0001,tol = 0.00001,batchSize = 100)
$weights
2.02646349019186 2.0439693915315
$iters
920064
小梯度批量梯度下降收敛时需要迭代92万次,这显然有点多了。一般来说,当数据量非常大时,小批量梯度下降比较有效,否则计算结果很有可能出现偏移。
先mark,偏移的原因待考究。
Momentum optimization
考虑这样一种情形,小球从山顶往下滚动,一开始很顺利,可是在接近最低点的时候,小球陷入了一段狭长的浅山谷。由于小球一开始并不是直接沿着山谷的方向滚下,因此小球会在这个浅浅的山谷中不断震荡——不断冲上墙壁,接着又从墙壁上滚下来。这种情况并不是我们想看到的,因为这增加了迭代时间。冲量(Momentnum)的引入,使得我们的目标更新的更快了,冲量的更新方式有以下两种,两种方式之间并无太大差异。
第一种:
\(Z^{k+1}=\beta Z_k + \nabla\)
\(w^{k+1} = w_k - \alpha Z^{k+1}\)
其中,\(Z\)是一个与\(w\)方向相同的向量,
第二种:
\(Z^{k+1}=\beta Z^k + \alpha \nabla\)
\(w^{k+1} = w^k - Z^{k+1}\)

两者的差别仅仅在于\(Z^{k+1}\)的系数不同。
通常,这里的学习率要比随机梯度下降小一点,因为随机梯度下降的梯度大一点。\(\beta\)的取值决定了前一次的梯度有多少被纳入了本次的更新。一般来说,稳定前将\(\beta\)设置为0.5,稳定后可以设置为0.9或更高。
#适用于求解一元或多元线性回归的回归系数,返回结果包括截距
momentumGradientDescent <- function(dat,beta = 0.9,z = 0,start = rep(0,dim(dat)[2]),alpha = 0.001,tol=0.0000001,iterations = 100)
{
dataSet = cbind(1,dat) #将第一列加上1
cols = dim(dataSet)[2] #列数
x = as.matrix(dataSet[,1:(cols - 1)]) #自变量矩阵
y = as.matrix(dataSet[,cols],ncol = 1) #因变量,矩阵
w = as.matrix(start,ncol = 1) #权重矩阵
iters = 0
while(TRUE)
{
old_w = w
old_z = z
Ypred = x %*% w
error = y - Ypred
grad = - t(x) %*% error
z = beta * old_z + grad
w = old_w - alpha * z
if(sum(abs(w-old_w)) < tol)
break;
iters = iters + 1
if(is.integer(iterations))
if(iters >= iterations)
break;
}
list(weights = as.vector(w),iters = iters)
}
利用冲量梯度下降求bigdata的系数:
momentumGradientDescent(bigdata,alpha=0.00001)
$weights
[1] 2.003851 2.006354
$iters
[1] 248
可以看到,迭代次数明显减少,并且系数与精确值更加接近了。
Nesterov Accelerated Gradient
然而,让一个小球盲目地沿着斜坡滚下山是不理想的。我们需要一个更聪明的球,它知道下一步要往哪里去,因此在斜坡有上升的时候,它能够自主调整方向。
Nesterov Accelerated Gradient 是基于冲量梯度下降算法进行改进的一种算法,也是梯度下降算法的变种。
在上一种算法中,我们使用了冲量\(\beta Z^k\)来调整我们的参数改变量,将上述第二种更新方法改写一下,得到如下式子:
\(Z^{k+1} = \beta Z^k + \alpha \nabla\)
$w^{k+1} = w^k - Z^{k+1} = w^k - \beta Z_k - \alpha \nabla $
$w^k - \beta Z_k $给出了下一个参数位置的近似,指明了参数该如何变化。现在,我们可以不用当前的参数,而是用未来的参数的近似位置来更新我们的参数,即
\(Z^{k+1} = \beta Z^k + \alpha \nabla _wJ(w - \beta Z^k)\)
\(w^{k+1} = w^k - Z^{k+1}\)
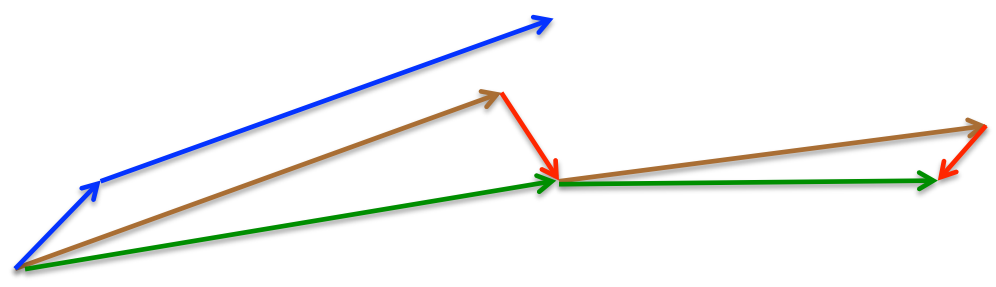
这里,我们仍然设置\(\beta\)的值在0.9附近。如下图所示,冲量梯度下降先计算当前的梯度(短的蓝色向量),然后根据累积的冲量向前跨越一大步(长的蓝色向量)。NAG首先根据之前的累积梯度向前迈一大步(棕色向量),然后对梯度进行修正(红色向量)。这种利用近似未来参数来更新参数的方法,可以防止梯度更新太快,并且增加了响应能力。
假设我们的权重矩阵(系数矩阵)为\(w\),自变量\(x\),因变量\(Y\),则损失函数为:
\[J(w) = 1/2 \sum _{i=1} ^n (Y_i - w'x_i)^2 \]则
\[\nabla J(w) = \frac{\partial J(w)}{\partial w} = - \sum_{i=1}^n(Y_i - w'x_i)x_i' \]那么
\[\nabla J(w - \beta Z^{k}) = - \sum _{i=1}^n(Y_i - (w'-\beta Z^k)'x_i)x_i' \]
根据上述思想,编写的NAG代码如下 :
#适用于求解一元或多元线性回归的回归系数,返回结果包括截距
NAG <- function(dat,beta = 0.9,z = 0,start = rep(0,dim(dat)[2]),alpha = 0.001,tol=0.0000001,iterations = 100)
{
dataSet = cbind(1,dat) #将第一列加上1
cols = dim(dataSet)[2] #列数
x = as.matrix(dataSet[,1:(cols - 1)]) #自变量矩阵
y = dataSet[,cols] #因变量,矩阵
w = start #权重矩阵
iters = 0
while(TRUE)
{
old_w = w
old_z = z
#中间过程用mid1 mid2代替
mid1 = apply((old_w - beta * old_z) * t(x),2,sum)
mid2 = y - mid1
grad = - apply(mid2 * x,2,sum)
z = beta * old_z + alpha * grad
w = old_w - z
if(sum(abs(w-old_w)) < tol)
break;
iters = iters + 1
if(is.integer(iterations))
if(iters >= iterations)
break;
}
list(weights = as.vector(w),iters = iters)
}
用NAG来求bigdata的系数:
NAG(bigdata,alpha=0.000001)
$weights
[1] 2.003849 2.006350
$iters
[1] 598
AdaGrad
尽管我们可以根据损失函数的梯度来加快更新参数,我们也希望能够根据参数的重要性来决定其更新的幅度。
AdaGrad是一种基于梯度算法的优化算法,它只做了一件事:根据参数来自适应调整学习率。对于不常出现的参数进行较大的更新,对于经常出现的参数进行较少的更新,因此,这种方法非常适合处理稀疏数据。
之前,我们对每一个参数更新所使用的学习率都是一样的,而AdaGrad在每一步都使用不同的学习率对不同的参数进行更新。我们先写出AdaGrad的单个参数的更新方法,然后将其向量化。长话短说,假设\(g_{t,i}\)表示损失函数对于参数\(\theta_i\)的梯度:
在步骤\(t\):
那么,对于步骤\(t\),使用随机梯度下将对\(\theta_i\)进行更新的公式为:
在上述更新过程中,AdaGrad在每一步都对参数\(\theta_i\)对应的学习率\(\eta_i\)进行调整,调整的方法基于过去的所有梯度:
\(G_{t}\in R^{d\times d}\)是一个对角矩阵,第\(i\)个对角元素是历史上损失函数对\(\theta_i\)的所有梯度的平方和,\(\epsilon\)是一个平滑参数,防止分母为0,通常取\(10^{-8}\)。有趣的是,如果不加开方,算法表现极差。
因为\(G_t\)包含了过去所有参数梯度的平方和,因此我们可以将其向量化:
AdaGrad的一个最大的好处是不用手动调整学习率的大小,通常设置默认值为0.01,然后顺其自然就好了。
AdaGrad的一个较大的缺点是,分母是不断增大的,当迭代次数不断增加时,分母会逐渐趋于无穷大,学习率进而趋于无穷小,此时,算法将变得不再有效。
我们延用上述符号来写出AdaGrad的函数。
#SGD为基础
AdaGrad <- function(dat,theta,learning_rate = 0.01,start = rep(0,dim(dat)[2]),tol = 0.000001,iterations = 1000)
{
dataSet = cbind(1,dat) #将自变量进行增广,第一列全为1
cols = dim(dataSet)[2] #列数
rows = dim(dataSet)[1] #行数
x = as.matrix(dataSet[,1:(cols - 1)]) #自变量矩阵
y = dataSet[,cols] #因变量,矩阵
g = 0
theta = start #权重矩阵
iters = 0
while(TRUE)
{
old_theta = theta
index = sample(rows)
for(i in index)
{
grad = - (y[i] - sum(theta * x[i,])) * x[i,]
g = g + grad * grad
theta = theta - learning_rate / sqrt(g + 1e-8) * grad
}
iters = iters + 1
if(is.integer(iterations))
if(iters > iterations)
break;
if(sum(abs(old_theta - theta)) < tol)
break;
}
list(weights = as.vector(theta),iters = iters)
}
AdaGrad的计算结果如下:
AdaGrad(bigdata)
$weights
[1] 2.008219 2.005682
$iters
[1] 6579
Adadelta
AdaDelta是在AdaGrad的基础上发展而来的,目的是解决AdaGrad算法中学习率的单调减少问题。AdaDelta不再采用累积梯度平方和的方法来调整学习率,而是根据一些固定的\(w\)的大小来限制过去累积梯度的窗口。
AdaDelta不再无效率地存储历史梯度的平方和,而将历史梯度平方和定义为衰减均值(decaying average)。第\(t\)步的移动平均值\(E[g^2]_t\)仅仅取决于过去的平均值和当前梯度(有点类似于momentum):
同样的,我们把\(\gamma\)设置在0.9附近。为清楚起见,我们重新写下更新规则:
\[\Delta \theta _t = - \eta \cdot g_{t,i} \]\[\theta _{t+1} = \theta_t + \Delta \theta _t \]
根据AdaGrad我们推出AdaDelta的参数更新公式:
\[\Delta \theta _t = - \frac{\eta}{\sqrt{G_t + \epsilon}} \odot g_t \]
我们只需把\(G_t\)替换\(E[g^2]_t\)就行了:
\[\theta_t = - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \]
因为分母刚好是梯度的均方根,我们将其简写为:
\[\Delta \theta_t = -\frac{\eta}{RMS[g]_t}g_t \]
作者们发现上述更新中的单位不一致(可以理解为量纲不一致),因此,他们定义了另外一个指数衰减均值,这次不用梯度的平方了,而是用参数的平方来进行更新:
参数更新的均方误差即:
因为\(RMS[\theta]_t\)是未知的,我们可以用之前所有的更新过的参数的RMS来代替。将之前的学习率\(\eta\)换成\(RMS[\Delta\theta]_{t-1}\),那么,我们得出AdaDelta的更新规则:
AdaDelta甚至不需要初始化学习率,因为在更新规则中已经不见它的身影了。
根据上述思路,我们写出AdaDelta的函数:
RMS <- function(x)
{
sqrt(mean(x^2) - mean(x)^2)
}
AdaDelta <- function()
RMSprop
Adam
上述所有改进方法均可以运用于批量梯度下降、小批量梯度下降和随机梯度下降!
【参考文献】
[1]http://netedu.xauat.edu.cn/jpkc/netedu/jpkc/gdsx/homepage/5jxsd/51/513/5308/530807.htm
[2]https://www.kdnuggets.com/2017/04/simple-understand-gradient-descent-algorithm.html


