kmeans聚类

聚类算法介绍

k-means算法介绍

k-means聚类是最初来自于信号处理的一种矢量量化方法，现被广泛应用于数据挖掘。k-means聚类的目的是将n个观测值划分为k个类，使每个类中的观测值距离该类的中心（类均值）比距离其他类中心都近。

k-means聚类的一个最大的问题是计算困难，然而，常用的启发式算法能够很快收敛到局部最优解。这通常与高斯分布的期望最大化算法相似，这两种算法都采用迭代求精的方法。此外，它们都使用聚类中心来对数据进行建模

k-means算法的提出与发展

詹姆斯·麦奎恩（James MacQueen）1967年第一次使用这个术语“k-means”，虽然这个想法可以追溯到1957年的雨果·斯坦豪斯（Hugo Steinhaus）。
标准算法首先由Stuart Lloyd在1957年提出，作为脉冲编码调制技术，尽管直到1982年才发布在贝尔实验室以外。
1965年，E. W. Forgy发表了基本相同的方法，这就是为什么它有时被称为Lloyd-Forgy。

k-means算法的优势适应问题

  • k-means算法优点

是解决聚类问题的一种经典算法，简单、快速。
对处理大数据集，该算法是相对可伸缩和高效率的。因为它的复杂度是\(O(nkt)\), 其中, n 是所有对象的数目, k 是簇的数目, t 是迭代的次数。通常\(k\ll n\)且\(t\ll n\) 。
当结果簇是密集的，而簇与簇之间区别明显时, 它的效果较好。

  • k-means算法缺点

在簇的平均值被定义的情况下才能使用，这对于处理符号属性的数据不适用。
必须事先给出k（要生成的簇的数目），而且对初值敏感，对于不同的初始值，可能会导致不同结果。
它对于“躁声”和孤立点数据是敏感的，少量的该类数据能够对平均值产生极大的影响。

k-means算法的思想介绍

(1) 选定某种距离作为数据样本件的相似性度量

由于k-means聚类算法不适合处理离散型数据，因此在计算个样本距离时，可以根据实际需要选择欧氏距离、曼哈顿距离或者明可夫斯基距离中的一种来作为算法的相似性度量。

假设给定的数据集\(X=\{x_m|m=1,2,...,total\}\),\(X\)中的样本用d个属性\(A_1,A_2,...,A_d\)来表示，并且d个描述属性都是连续型数据。数据样本\(x_i=(x_{i1},x_{i2},x_{id}),x_j=(x_{j1},x_{j2}...,x_{jd})\)，其中，\(x_{i1},x_{i2},x_{id}\)和\(x_{j1},x_{j2}...,x_{jd}\)分别是样本\(x_i\)和\(x_j\)对应的d个描述属性\(A_1,A_2,...,A_d\)的具体取值。样本\(x_i\)和\(x_j\)之间的相似度通常用他们之间的距离d(\(x_i,x_j\))来表示，距离越小，样本\(x_i\)和\(x_j\)越相似，差异度越小。距离越大，样本\(x_i\)和\(x_j\)越不相似，差异越大。
欧氏距离公式如下：

\[d(x_i,x_j)=\sqrt{\sum_{k=1}^d(x_{ik}-x_{jk})^2} \]

曼哈顿距离如下：

\[d(x_i,x_j)=\sum_{k=1}^d|x_{ik}-x_{jk}| \]

明可夫斯基距离如下：

\[d(x_i,x_j)=\sqrt[p]{\sum_{k=1}^d|x_{ik}-x_{jk}|^p} \]

当\(p=1\)时，明氏距离即为曼哈顿距离，当\(p=2\)时，明氏距离即为欧氏距离，当\(p=\infty\)时，明氏距离即为切比雪夫距离。

(2) 选择评价聚类性能的准则函数

k-means聚类算法使用误差平方和准则函数来评价聚类性能。给定数据集X，其中只包含描述属性，不包含类别属性。假设X包含k个聚类子集\(X_1,X2,...,X_k\),各个聚类子集中的样本量分别为\(n_1,n_2,...,n_k\)，各个聚类子集均值代表点分别为\(m_1,m_2,...,m_k\)，则误差平方和准则函数公式为：

\[E=\sum_{i=1}^k \sum_{p\in X_i}(p-m_i)^2 \]

(3) 相似度的计算根据一个簇中对象的平均值来进行

  1. 将所有对象随机分配到k个非空的簇中。

  2. 计算每个簇的平均值，并用该平均值代表相应的簇。

  3. 根据每个对象与各个簇中心的距离，分配给最近的簇。

  4. 然后转2，重新计算每个簇的均值。这个过程不断重复知道满足某个准则函数为止。

k-means实现流程：分步骤写

k-means算法2个核心问题，一是度量记录之间的相关性的计算公式，此处采用欧氏距离。一是更新簇内质心的方法，此处用平均值法，即means。
此时的输入数据为簇的数目k和包含n个对象的数据库——通常在软件中用数据框或者矩阵表示。输出k个簇，使平方误差准则最小。
下面为实现k-means聚类的Python代码

# (1)选择初始簇中心。
# (2)对剩余的每个对象，根据其与各个簇中心的距离，将它赋给最近的簇。
# (3)计算新的簇中心。
# (4)重复(2)和(3)，直至准则函数不再明显变小为止。
from numpy import *

#定义加载数据的函数。如果数据以文本形式存储在磁盘内，可以用此函数读取
def loadDataSet(fileName)
dataMat = []
fr = open(fileName)
for line in fr.readlines()
curLine = line.strip().split('\t')
fltLine = list(map(float,curLine))
dataMat.append(list(fltLine))
return dataMat

#该函数计算两个向量的距离，即欧氏距离
def distEclud(vecA,vecB)
return sqrt(sum(power(vecA - vecB,2)))

#曼哈顿距离
def Manhattan(vecA,vecB)
return sum(abs(vecA-vecB))

#明考夫斯基距离
def MinKowski(vecA,vecB,p)
return power(sum(power(abs(vecA-vecB),p)),1/p)

#此处为构造质心，而不是从数据集中随机选择k个样本点作为质心，
#也是比较合理的方法
def randCent(dataSet,k)
    n = shape(dataSet)[1]  #n为dataSet的列数
    centroids = mat(zeros((k,n)))  #构造k行n列的矩阵，就是k个质心的坐标
    for j in range(n)  #
        minJ = min(dataSet[,j])  #该列数据的最小值
        maxJ = max(dataSet[,j])  #该列数据的最大值
        rangeJ = float(maxJ-minJ)  #全距
        #随机生成k个数值，介于minJ和maxJ之间，填充J列
        centroids[,j] = minJ + rangeJ * random.rand(k,1)  
      
    return centroids
   
#定义kMeans函数 
def kMeans(dataSet,k,distMeas=distEclud,createCent=randCent)
    m = shape(dataSet)[0]  #m为原始数据的行数
    #clusterAssment包含两列，一列记录簇索引值，一列存储误差
    clusterAssment = mat(zeros((m,2)))  
    centroids = createCent(dataSet,k)  #构造初始的质心
    clusterChanged = True  #控制变量
    while clusterChanged  #当控制变量为真时，执行下述循环
        clusterChanged = False  
        for i in range(m)   
            minDist = inf  #首先令最小值为无穷大 
            minIndex = -1  #令最小索引为-1
            for j in range(k)  #下面是一个嵌套循环
             #计算点数据点I和簇中心点J的距离
                distJI=distMeas(centroids[j,],dataSet[i,])
                if distJI < minDist  
                    minDist = distJI
                    minIndex = j
            if clusterAssment[i,0] != minIndex
                clusterChanged = True
            clusterAssment[i,] = minIndex,minDist**2
        print(centroids)
        #更新质心的位置
        for cent in range(k)
        #mat.A意味着将矩阵转换为数组，即matrix-->array
            ptsInClust = dataSet[nonzero(clusterAssment[,0].A==cent)[0]]
            centroids[cent,] = mean(ptsInClust,axis=0)
    return centroids,clusterAssment

k-means与EM算法

EM是机器学习十大算法之一，是一种好理解，但是推导过程比较复杂的方法。
下面将原英文版的EM算法介绍翻译一遍，在翻译的过程中也加深一点自己的理解。

Jensen不等式

假设\(f\)是一个定义域为实数的函数。回忆一下，如果对于所有的\(x \in R,f''(x) \geq 0\)，则\(f\)是一个凸函数。 如果\(f\)的输入值是一个向量，则当\(x\)的海塞矩阵(hessian矩阵\(H\))是半正定矩阵时，\(f\)是凸函数。如果对于所有的\(x\)，\(f''(x)>0\)恒成立，那么我们说\(f\)是严格凸函数（如果\(x\)是一个向量，则当\(H\)是严格半正定矩阵时，写做\(H>0\)，则\(f\)是严格凸函数）。
设\(f\)是一个凸函数，并且\(X\)是一个随机变量，则：

\[E[f(X)] \geq f(EX). \]

当且仅当\(x=\)常数时，\(E[f(X)]=f(EX)\)\(.\)
进一步说，如果\(f\)是一个严格凸函数，则当P{X=E(X)}=1时，满足\(E[f(X)] = f(EX).\)

由于我们在写某一随机变量的期望时，习惯上是不写方括号的，因此在上述式子中，\(f(EX)=f(E[X])\)
为了解释上述理论，可以用图1帮助理解。

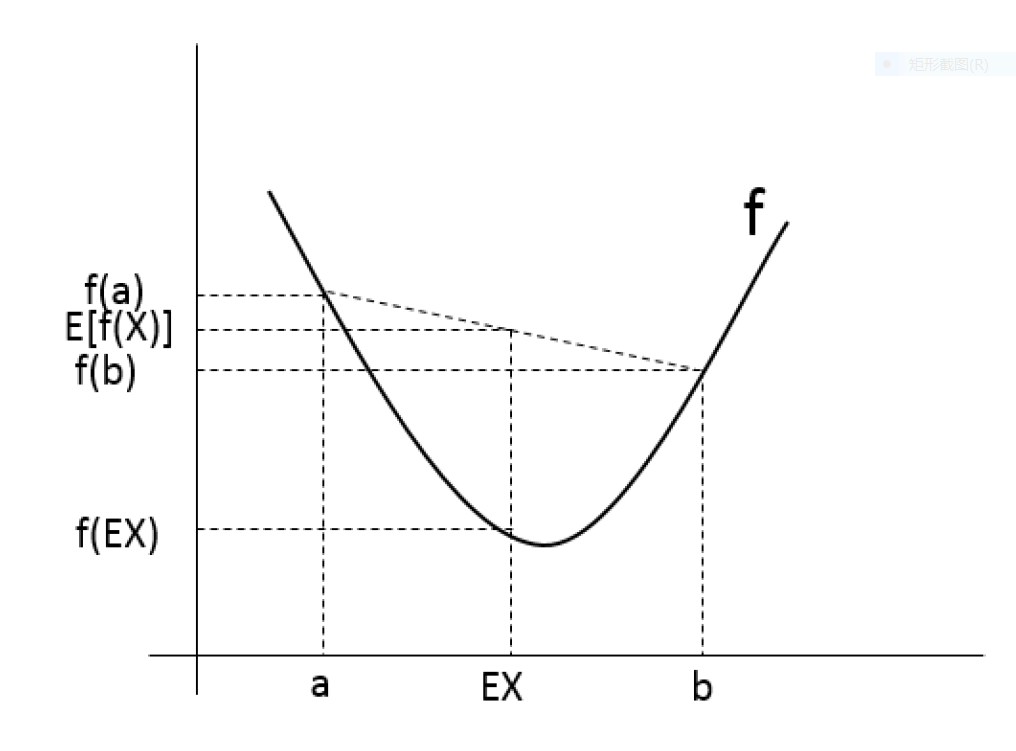
如图1所示，实黑线表示凸函数\(f\)，\(X\)是一个随机变量，取值为\(a\)和\(b\)的概率均为0.5。因此，\(a\)和\(b\)的均值\(E(X)\)在二者之间。

与此同时，我们在y轴上可以看见\(f(x)\),\(f(b)\)和\(f(EX)\)的值，并且，\(E[f(X)]\)\(f(a)\)和\(f(b)\)之间。从这个例子可以看出，因为\(f\)是一个凸函数，所以肯定满足\(E[f(X)]\ge f(EX)\)。
一般来说，很多人会忘记上式的不等号方向，那么，记住这个图，就很易能够想起来上面的公式了。

注意，如果\(f\)是一个(严格的)凹函数(\(f''(x)\le 0\)或者\(H\le0\))，Jensen不等式仍然成立，只是方向反过来而已，即\(E[f(X)]\le f(EX).\)}

EM算法

假设我们有包含m个独立样本的训练集\(\{x^{(1)},x^{(2)},...,x^{(m)}\}\),基于该样本和模型\(p(x,z)\)估计待估参数\(\theta\),似然函数如下：

\[\ell (\theta)=\sum _{i=1}^mlogp(x;\theta)=\sum _{i=1}^mlog\sum _zp(x,z;\theta). \]

但是，明确找出\(\theta\)的最大似然估计值恐怕非常困难。因为在这里，\(z^{(i)}\)是隐含随机变量，通常情况下如果已知\(z^{(i)}\)，那么求上述最大似然估计值会比较容易。

在这种情况下，EM算法给出了一种有效的求最大似然估计值的方法。直接求\(\ell (\theta)\)的最大似然估计值也许会很困难，我们的策略是在\(\ell (\theta)\)下面构造一个下界(E-步骤)，然后优化这个下界，使其不断逼近求\(\ell (\theta)\)的最大似然估计值(M-步骤)。

对于每一个\(i\)，令\(Q_i\)是\(z^{(i)}\)上关于某一分布的概率，(\(\sum _zQ_i(z)=1,Q_i(z)\ge 0\)).}得到下面的式子.如果z是连续型随机变量，那么\(Q_i\)就是密度函数，\(Q_i\)在z上的总和就是\(Q_i\)在z上的积分：

\[\sum _i logp(x^{(i)};\theta)=\sum _ilog\sum _{z^{(i)}} p(x^{(i)},z^{(i)};\theta) \]

\[=\sum _i log \sum _{z^{(i)}}Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]

\[\ge \sum _i \sum _{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\]

最后一步应用了Jensen不等式。特别地，在这里\(f(x)=logx\)是一个凹函数，因为在实数范围内

\[f''(x)=-1/x^2<0 \]

式子

\[\sum _{z^{(i)}}Q_i(z^{(i)})[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}] \]

是式子的\([p(x^{(i)},z^{(i)};\theta)/Q_i(z^{(i)})]\)关于\(z^{(i)}\)在\(Q_i\)给出的分布上的期望。根据Jensen不等式，有：

\[f(E_{z^{(i)}\sim Q_i}[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}])\ge E_{z^{(i)}\sim Q_i}[f(\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})})] \]

下标\(z^{(i)}\sim Q_i\)表示期望是对来自于分布\(Q_i\)的随机变量\(z^{(i)}\)所求的期望。这个条件使式子(2)到式子(3)得以成立。

现在，对于来自于\(Q_i\)的任意一个集合，式子(3)给出了一个\(\ell (\theta)\)的一个下界。\(Q_i\)有很多种可能的选择，我们应该选哪个呢?如果我们当前对参数\(\theta\)(基于已有的条件)已经有了一些猜测，那么使这个下界与\(\theta\)的值接近看起来就比较自然了。换句话说，我们可以使上述的不等式在\(\theta\)的某个特定值的条件下变成等式。(稍后我们就能看到上述是何如使\(\ell (\theta)\)在EM的迭代下单调递增的。)

为了使下界尽可能地靠近\(\theta\)的某个特定值，我们需要在步骤中加入上面推导的Jensen不等式以得到等式。为了实现上述步骤，我们知道只需要使期望变成常量——固定的随机变量就行了。例如，我们需要满足：

\[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=c \]

而这个常数\(c\)不依赖于\(z^{(i)}\)。这个很简单就可以实现，只需要使

\[Q_i(z^{(i)})\propto p(x^{(i)},z^{(i)};\theta) \]

实际上，因为我们已知\(\sum _zQ_i(z^{(i)})=1\),所以有：

\[Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum _zp(x^{(i)},z^{(i)};\theta)} \]

\[=\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} \]

\[=p(z^{(i)}|x^{(i)};\theta) \]

因此，我们简单假设\(Q_i\)是在给定\(x^{(i)}\)和参数\(\theta\)的情况下\(z^{(i)}\)的后验概率.

现在，对于上述的\(Q_i\)，公式(3)给出了我们想取极大值的似然函数\(\ell\)的下界。这是E步骤。在算法里的M步骤，我们又对公式(3)取极大值以获得新的\(\theta\).重复执行上述步骤，即：

start循环直到收敛

(E-step)对于每一个i,令：

\[Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\theta) \]

M-step 令：

\[\theta=arg\ max_\theta \sum _i \sum _{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]

我们怎么知道这个算法最终收敛呢？假设\(\theta^{(t)}\)和\(\theta^{(t+1)}\)是EM算法连续迭代两次以后得到的参数。下面证明\(\theta^{(t)} \le \theta^{(t+1)}\)，即证明EM算法会使log似然概率单调递增。证明上述的关键是对于\(Q_i\)的选择。在以\(\theta^{(t)}\)为起始标志的EM算法迭代过程中，我们会选择\(Q_i^{(t)}(z^{(i)})=p(z^{(i)}|x^{(i)};\theta^{(t)})\).我们在前面已经看到了，上述选择会满足Jensen不等式，像公式(3)的应用一样，能够得到收敛的等式，即：

\[\ell (\theta^{(t)})=\sum _i \sum _{z^{(i)}}Q_i^{(t)}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} \]

最大化等式右边得到参数\(\theta^{(t+1)}\)，因此：

\[\ell (\theta^{(t+1)})\ge \sum _i \sum _{z^{(i)}}Q_i^{(t)}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i^{(t)}(z^{(i)})} \]

\[ \ge \sum _i \sum _{z^{(i)}}Q_i^{(t)}(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i^{(t)}(z^{(i)})} =\ell (\theta^{(t)}) \]

第一个不等式来自于：

\[ \ell(\theta) \ge \sum _i \sum _{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]

上式对于\(Q_i\)和\(\theta\)的任意值，尤其是\(Q_i=Q_i^{(t)}\),\(\theta=\theta^{(t+1)}\)时成立。为了得到不等式(5)，我们依据的是\(\theta^{(t+1)}\)应该等于：

\[ arg\ max_\theta \ \sum _i \sum _{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \]

因此根据上式计算的\(\theta^{(t+1)}\)肯定是大于等于\(\theta^{(t)}\)的。最后，自然而然就推到了公式(6).

因此，EM使得似然函数单调收敛。我们们关于EM算法的描述中，我们说最终似然函数会收敛。尽管我们的结果已经展示了上述结论，但是一个令人信服的收敛性检验将会检查在给定的参数容忍度的情况下，

\(\ell(\theta)\)会随着EM算法的迭代而不断增加，如果EM使得\(\ell(\theta)\)的上升速度慢到一定程度，就意味着收敛。

如果我们定义

\[ J(Q,\theta)=\sum _i \sum _{z^{(i)}}Q_i(z^{(i)})log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} ,\]

在我们前面的推导中已经知道了\(\ell (\theta)\ge J(Q,\theta)\)。EM算法还可以看作使畸变函数J不断上升的过程。E-step固定Q，最大化J；M-step固定\(\theta\)最大化J。而Q和\(\theta\)都是在迭代过程中不断更新的。

k-means与EM

在1.8.4节对k-means算法的迭代思想进行了说明，可以看出与EM算法具有很大的相似性，在原理上几乎相同。

k-means举例及R实现

本文以R自带数据集iris为例，实现聚类的k-means算法。首先，看一下iris数据集的基本结构，如表1所示。

| Sepal.Length | Sepal.Width | Petal.Length | Petal.Width | Species
-|-|-|-|-|-
1 | 5.10 | 3.50 | 1.40 | 0.20 | setosa
2 | 4.90 | 3.00 | 1.40 | 0.20 | setosa
3 | 4.70 | 3.20 | 1.30 | 0.20 | setosa
4 | 4.60 | 3.10 | 1.50 | 0.20 | setosa
5 | 5.00 | 3.60 | 1.40 | 0.20 | setosa
6 | 5.40 | 3.90 | 1.70 | 0.40 | setosa

该数据集共有5个变量，表1显示的是前6行的数据，完整数据一共有150行。五个变量的中文名称分别是：萼片长度、萼片宽度、花瓣长度、花瓣宽度和品种。以此样本作为聚类的原始数据，属于有标签聚类，可以将聚类结果与真实情况进行对比，以得出聚类效果。
下面是实现k-means聚类的R语言代码：

> iris_test<-iris[,14]
> iris_test_cl<-kmeans(x = iris_test,centers = 3,iter.max = 20)
> iris_test_cl
K-means clustering with 3 clusters of sizes 50, 62, 38

Cluster means
  Sepal.Length Sepal.Width Petal.Length Petal.Width
1     5.006000    3.428000     1.462000    0.246000
2     5.901613    2.748387     4.393548    1.433871
3     6.850000    3.073684     5.742105    2.071053

Clustering vector
  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 [39] 1 1 1 1 1 1 1 1 1 1 1 1 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [77] 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3 3 2 3 3 3 3 3 3 2
[115] 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 3 3 3 3 2 3 3 3 2 3 3 3 2 3 3 2

Within cluster sum of squares by cluster
[1] 15.15100 39.82097 23.87947
 (between_SS / total_SS =  88.4 %)

Available components

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      
> table(iris_test_cl$cluster,iris$Species)
   
    setosa versicolor virginica
  1     50          0         0
  2      0         48        14
  3      0          2        36

根据输出结果可以看出，setosa类分类正确率为100%，versicolor类有48个分类正确，有两个错误分到了virginica中，viginica有36个分类分类正确，有14个错误分到了versicolor中。总体来说，聚类的正确率为89.3%

k-means算法的改进

k-mode算法

k-mode算法实现了对离散型数据的快速聚类，保留了k-means算法的效率的同时，将k-means的应用范围扩大到了离散型数据。

k-mode算法是按照k-means算法的核心内容进行修改，针对分类属性的度量和更新质心的问题而改进。具体如下：

度量记录之间的相关性D的计算公式是比较两记录之间，属性相同为0，不同为1，并把所有的值相加。因此D越大，就说明两个记录之间的不相关性越强，也可以理解为距离越大，与欧氏距离代表的意义是一样的。
更新modes，使用每个簇的每个属性出现频率最大的那个属性值作为代表簇的属性值。

k-prototype算法

k-prototype算法可以对离散型和数值型两种混合的数据进行聚类，在k-prototype中定义了一个对数值型和离散型属性都计算的相异性度量标准。

k-prototype是结合k-means和k-mode算法，针对混合属性的，解决两个核心问题如下：

度量具有混合属性的方法是，数值型属性采用k-means方法得到P1，分类属性采用k-mode方法得到P2，那么D=P1+a*P2，a是权重，如果觉得分类属性重要，则增加权重的值。当a=0时，只有数值型属性。
更新一个簇的中心的方法是结合k-means和k-mode的方法。

k-中心点算法

k-中心点算法是针对k-means算法对于孤立点敏感所提出的改进方法。为了解决上述问题，不采用簇中的平均值作为参照点，可以选用簇中位置最中间的对象，即中心点作为参照点。这样划分方法仍然基于最小化所有对象与其参照点的相异度之和的原则来执行的。
对于算法的实现来说，就是在更新质心的时候，不是计算所有点的平均值，而是中位数来代表其中心。然后进行迭代，直到质心不再变化为止。

Enhanced k-means

下面讨论一下k-means聚类的收敛性。

任意生成k个初始类中心\(\mu_1,\mu_2,...,\mu_k \in R\).

重复如下步骤直到收敛：

对于每一个i，令

\[c^{(i)}=arg \ {min_j ||x^{(i)}-\mu_j||^2} \]

对于每一个j，令

\[\mu_j=\frac{\sum _{i=1}^m1\{c^{(i)}=j\}x^{(i)}} {\sum _{i=1}^m1\{c^{(i)}=j\}} \]

那么，k-means算法是否能够保证一定收敛呢？答案是肯定的。
定义畸变函数

\[J(c,\mu)=\sum _{i=1}^n||x^{(i)}-\mu _c^{(i)}||^2 \]

k-means算法的目的就是使J降至最小。在内循环中，固定\(\mu\),可以通过调整\(c\)来使J减小；同样的，固定\(c\)，调整每个类的质心\(\mu\)也可以使J减小。当J减到最小时，\(\mu\)和\(c\)也同时收敛。

但是，需要注意的是，J函数是一个非凸函数，所以J不能保证收敛到全局最优，而可以保证收敛到局部最优。通常，k-means达到局部最优的结果差不多是全局最优。但是如果担心陷入了很严重的局部最优，可以多运行几次k-means算法（(给出不同的初始类中心)，选出使J达到最小值的那个模型的\(\mu\)和\(c\)。

为了克服k-means上述缺点，可以在k-mean的结果上对其进行改进(enhanced k-means)。该算法步骤如下：

根据k-means算法得出k个类和相应的类中心。

计算每一个样本点与所有类中心的欧氏距离。

假设\(x_i\)在第\(r\)个类中，\(n_r\)表示第\(r\)个类包含的样本点数目，\(d_{ir}^2\)表示\(x_i\)与第\(r\)个类的中心点的欧氏距离。如果存在类\(s\)，使得

\[\frac{n_r}{n_r-1}d_{ir}^2>\frac{n_s}{n_s+1}d_{is}^2, \]

则将\(x_i\)移到类\(s\)中。
如果有多个类满足上述不等式，则将\(x_i\)移动到使得
\(\frac{n_s}{n_s+1}d_{ir}^2\)最小的那个类中。
重复步骤2$\sim$4，直到没有变化为止。

二分K-均值算法

为了克服k-means算法收敛于局部最小值的问题，有人提出了使用另一个称为二分-K均值(bisecting K-means)的算法。该算法首先将所有的点作为一个簇，然后将该簇一分为二。之后选择其中一个簇继续划分，选择哪一个簇进行划分取决于对其划分是否可以最大程度降低SSE的值。上述基于SSE的划分过程不断重复，直到得到用户指定的簇数目为止。

二分K-均值算法的步骤如下：

将所有的点看成一个簇
当簇数目小于k时，对于每一个簇

计算总误差
在给定的簇上面进行K-means聚类(k=2)
计算将该簇一分为二后的总误差

选择使得误差最小的那个簇进行划分操作。

另一种方法是选择SSE最大的那个簇进行划分。该算法的R代码如下。

#计算误差平方和SSE，group接受一个数值型矩阵，centroid为其均值向量


SSE<-function(group,centroid)
{
  rows= nrow(group)
  group = as.matrix(group)
  centroid = matrix(rep(centroid,rows),nrow = rows,byrow = TRUE)
  group = group - centroid
  group = group * group
  sums = apply(X = group,MARGIN = 1,FUN = sum)
  SSE = sum(sums)
  return(SSE)
}
#定义二分K-means聚类函数，dataSet为需要聚类的数据集，k为指定聚类个数
biKmeans<-function(dataSet,k)  
{
  if(!is.matrix(dataSet))
    dataSet = as.matrix(dataSet)
  if(k==1)
    return(dataSet)
  else
  {
    #定义一个空矩阵来存放不需要再次处理的已经聚好的类
    clusteredDataSet = matrix(nrow = 0,ncol = ncol(dataSet))
    #定义一个空向量用来存放上述类的标签
    clustered = vector(length = 0)
    #计数器clusters
    clusters = 1
    #i用来改变每次聚类的标签
    i = 0
    while(clusters < k)
    {
      #使用k-means用来二分聚类
      cl = kmeans(dataSet,2)
      #类标签
      cluster = cl$cluster+i
      #计算聚好的两个类的与类中心的离差平方和
      SSE1 = SSE(group = dataSet[cluster==(1+i),],centroid = cl$centers[1,])
      SSE2 = SSE(group = dataSet[cluster==(2+i),],centroid = cl$centers[2,])
      #将误差平方和大的拿出来，下次继续二分
      if(SSE1 > SSE2)
        index = (cluster == (1+i))
      else
        index = (cluster ==(2+i))
      #将不需要再次聚类的类放在clusterDataSet例
      clusteredDataSet = rbind(clusteredDataSet,dataSet[!index,])
      #将上述类的标签存放在clustered里
      clustered = c(clustered,cluster[!index])
      #更新dataSet，下次继续二分
      dataSet = dataSet[index,]
      #计数器+1
      clusters = clusters +1
      #i+2，因为每次二分的结果是1和2，在结果的基础上加上2，则类标签可以明确区分
      i = i + 2
    }#end while
    #得出最终聚类结果
    clusteredDataSet = rbind(clusteredDataSet,dataSet)
    #类标签
    clustered = c(clustered,cluster[index])
    #转换为数据框
    clusteredDataSet = as.data.frame(clusteredDataSet)
    #添加类标签列
    clusteredDataSet$cluster = clustered
    return(clusteredDataSet)
  }
}
> iris_test_bik<-biKmeans(iris_test,3)
> dim(iris_test_bik)
[1] 150   5
> table(iris_test_bik$cluster,iris$Species)
   
    setosa versicolor virginica
  1     50          3         0
  3      0          9        50
  4      0         38         0

由上述最终的聚类结果显示，聚类正确率约为92%，比单纯使用k-means算法正确率高。

Enhanced k-means算法更加稳健的原因

k-means算法具有明显的两个缺点，即容易陷入局部最优和出现“超级类”。局部最优比较好理解，“超级类”是指聚类结果中有一个包含许多样本点的大类，其他的类包含的样本点都较少。enhanced k-means同时考虑了样本点与聚类中心的距离和类中样本点的个数，保留了k-means聚类算法的优点，同时又克服了出现"超级类"的问题。

Enhanced k-means举例及R实现

k-中心点算法可以使用R中cluster包中的pam函数(pam的全称为Partitioning Around Medoids，即围绕中心点分割)，同样以iris数据集为例，说明pam函数的使用。

> library(cluster)
> pam.cl<-pam(iris_test,k = 3)
> table(pam.cl$clustering,iris$Species)
   
    setosa versicolor virginica
  1     50          0         0
  2      0         48        14
  3      0          2        36
> par(mfrow=c(1,2))
> plot(pam.cl)

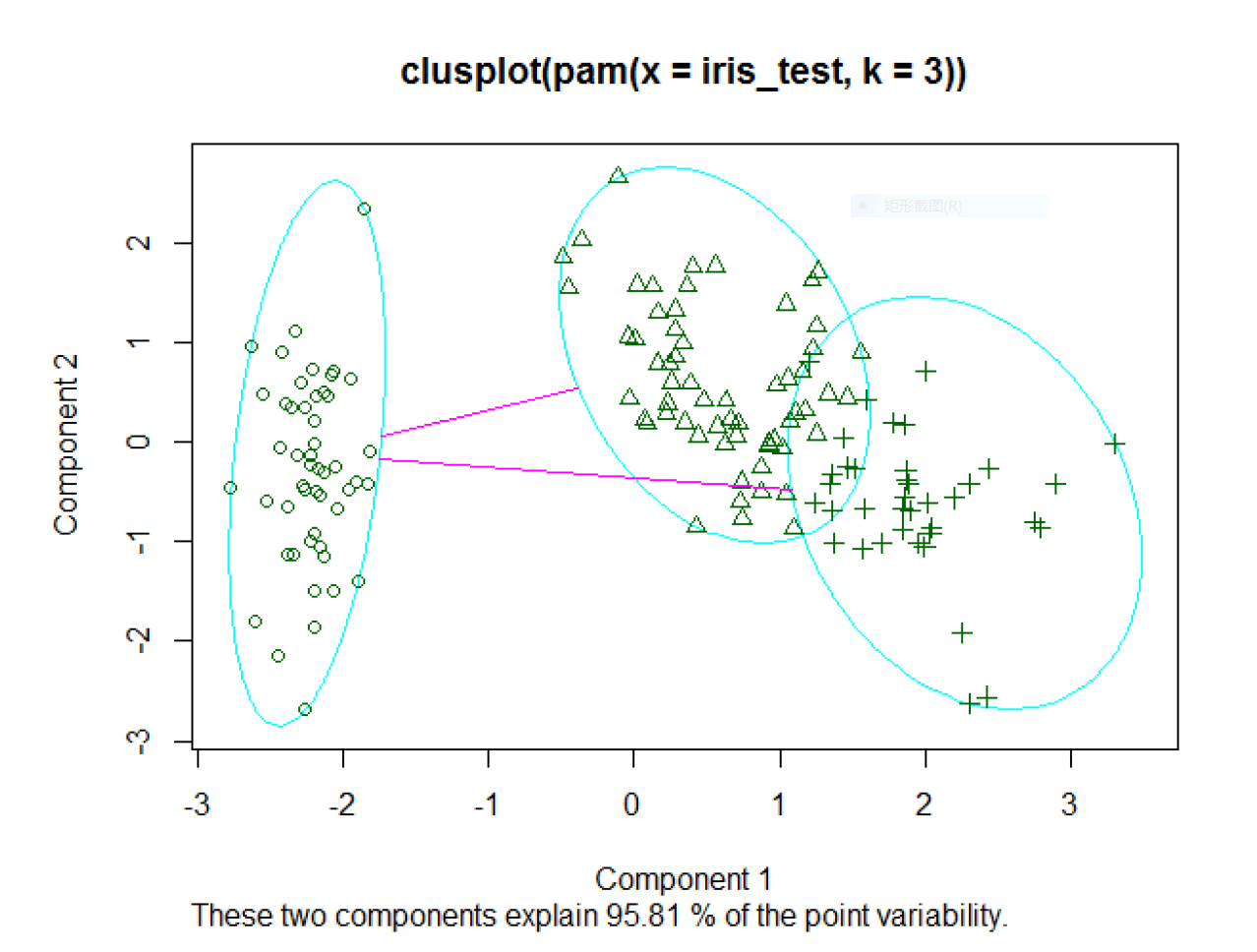
图2将原始数据进行了降维，提取了两个主成分，并且这两个主成分能够解释原始数据方差的95.81%，说明降维效果很好。将这两个成分绘制成散点图，就得到了图2.结合table函数的输出结果和图2可知，setosa类与其他两个类的界限比较明显，而其他两个类之间具有交叉。


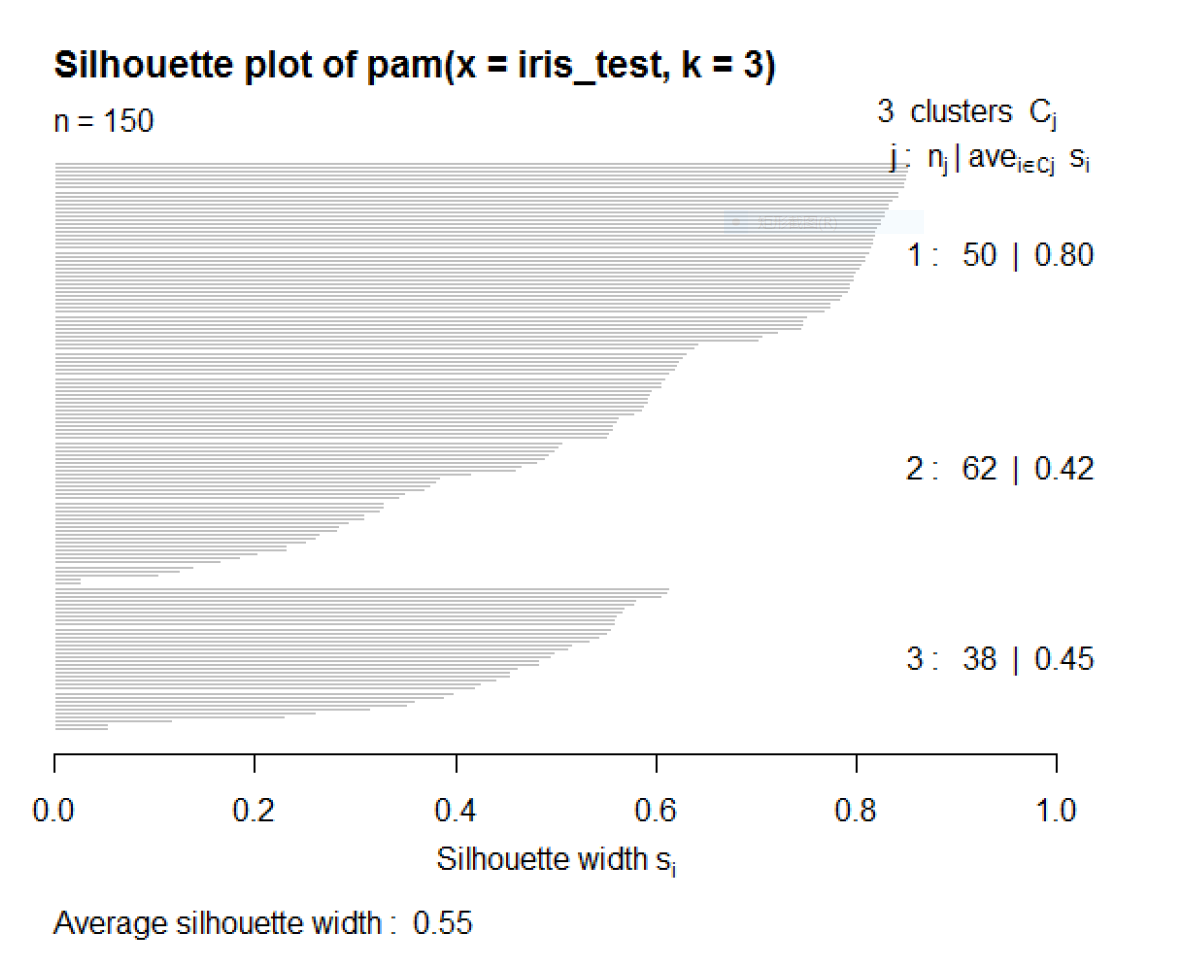
kmeans_4.PNG
kmeans_4.PNG

聚类指标评价

多种聚类结果的比较

聚类性能的度量大致有两类，一类是将聚类结果与某个“参考模型”进行比较，称为“外部指标”；另一类是直接考察聚类结果而不利用任何参考模型，称为“内部指标”。

外部指标

对数据集\(D=\{x_1,x_2,...,x_m\}\),假定通过聚类给出的簇划分为

\[C=\{C_1,C_2,...,C_k\}, \]

参考模型给出的簇划分为

\[C^+=\{C_1^+,C_2^+,...,C_s^+\} \]

相应地，令 \(\lambda\) 与 \(\lambda^+\) 分别表示与 \(C\) 和 \(C^+\) 对应的簇标记向量，我们将样本两两配对考虑，定义

\[a=|SS|,SS=\{(x_i,x_j)|\lambda _i=\lambda _j,\lambda _i^+=\lambda _j^+,i<j \} \]

\[b=|SD|,SD=\{(x_i,x_j)|\lambda _i =\lambda _j,\lambda _i^+ \ne \lambda _j^+,i<j \} \]

\[c=|DS|,DS=\{(x_i,x_j)|\lambda _i \ne \lambda _j,\lambda _i^+=\lambda _j^+,i<j \} \]

\[d=|DD|,DD=\{(x_i,x_j)|\lambda _i \ne \lambda _j,\lambda _i^+ \ne \lambda _j^+,i<j \} \]

其中集合\(SS\)包含了在\(C\)中隶属于相同簇且在\(C^+\)中也隶属于相同簇的样本对，集合\(SD\)包含了在\(C\)中隶属于相同簇但在\(C^+\)中隶属于不同簇的样本对，……由于每个样本对 \((x_i,x_j)(i<j)\) 仅能出现在一个集合中，因此有 \(a+b+c+d=m(m-1)/2\)成立。

基于以上给出的信息，可以导出下面常用的聚类性能度量外部指标。

Jaccard系数(Jaccard Coefficient,简称JC)

\[JC=\frac{a}{a+b+c}. \]

FM指数(Fowlkws and Mallows Index,简称FMI)

\[FMI=\sqrt{\frac{a}{a+b}\times \frac{a}{a+c}}. \]

Rand指数(Rand Index,简称RI)

\[RI=\frac{a+d}{m(m-1)/2}=\frac{a+d}{C_m^2}. \]

显然，上述性能度量的结果均在[0,1]之间，值越大越好。}

内部指标

考虑聚类结果的划分\(C=\{C_1,C_2,...,C_k\}\),定义：

\[avg(C)=\frac{2}{|C|(|C|-1)} \sum _{1\le i<j \le |C|}dist(x_i,x_j), \]

\[diam(C)=max_{1\le i<j \le |C|}dist(x_i,x_j), \]

\[d_{min}(C_i,C_j)=min_{x_i\in C_i,x_i\in C_j}dist(x_i,x_j), \]

\[d_{cen}(C_i,C_j)=dist(\mu _i,\mu _j), \]

其中，\(dist(·,·)\) 用于计算两个样本之间的距离，\(\mu\)代表\(C\)的中心点\(\mu =\frac{1}{|C|}\sum _{1\le i \le |C|}x_{i}.\)显然，\(avg(C)\)对应于\(C\)内样本间的平均距离，\(diam(C)\)对应于簇\(C\)内样本间的最远距离，\(d_{min}(C_i,C_j)\)对应于簇\(C_i\)与簇\(C_j\)最近样本间的距离，\(d_{cen}(C_i,C_j)\)对应于簇\(C_i\)与簇\(C_j\)中心点的距离。

基于上式可以导出下面这些常用的聚类性能度量内部指标。

DB指数(Davies-Bouldin Index,简称DBI)

\[DBI=\frac{1}{k}\sum _{i=1}^k max_{j\ne i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu _i,\mu _j)}). \]

Dunn指数(Dunn Index，简称DI)

\[DI=min_{1\le i \le k}\{min_{j\ne i}(\frac{d_{min}(C_i,C_j)}{max_{1\le l \le k}\ diam(C_l)})\} \]

显然，DBI的值越小越好，而DI则相反，值越大越好。

共表型相关系数

共表型相关系数(Cophenetic Correlation Coefficient，简称CPCC)

内容参考：http//people.revoledu.com/kardi/tutorial/Clustering/index.html.

另外，共表相关系数也属于内部指标，这里单独拿出来是因为其计算比较复杂，且仅仅用在层次聚类方法上。共表型相关系数是用于衡量层次聚类聚类性能的指标，为了清楚说明共表相关系数的计算，下面先从层次聚类说起。
层次聚类的标准输出结果是一个树状图，树状图的横坐标显示的是样本点，纵坐标是树的高度。树状图可以看作是层次聚类的可视化结果。

使用树状图，我们可以很容易地找出决定聚类个数的分割点。比如说，在图4中，如果将分割高度设置为2，则将6个样本聚成2类(一类包含了A、B样本，一类包含了C、E、D、F)；如果将分割高度设置为1.2，则将6个样本聚成3类(一类包含A、B，一类包含C，一类包含E、D、F)。

层次聚类算法一共有两种实现方法。第一种方法是\(agglomerative \ approach\)，先从底部将所有的样本点单独看作一类，然后将两个最近的样本点聚在一起，形成一个新的类。接着计算所有类之间的聚类，将两个最近的类聚在一起。上述步骤重复下去，直到把所有的点聚为一类。该方法也称为自底向上的层次聚类方法。第二种方法是\(divisive\ approach\)，即先从顶部开始，将所有的样本点看作一个大类。然后将该大类分成两个小类，直到所有的样本点自成一类结束。上述层次聚类的一个可行的方法是先将上述所有样本生成一个最小生成树(例如使用Kruskal算法)，然后通过最大距离将该树分割。这种方法也被称为自顶向下的层次聚类方法。

这里使用第一种方法演示层次聚类方法，步骤如下：

计算各个变量之间的聚类，生成距离矩阵

将每个样本点视为一个类

迭代，直到类的个数为1

将最近的两个类合并

更新距离矩阵

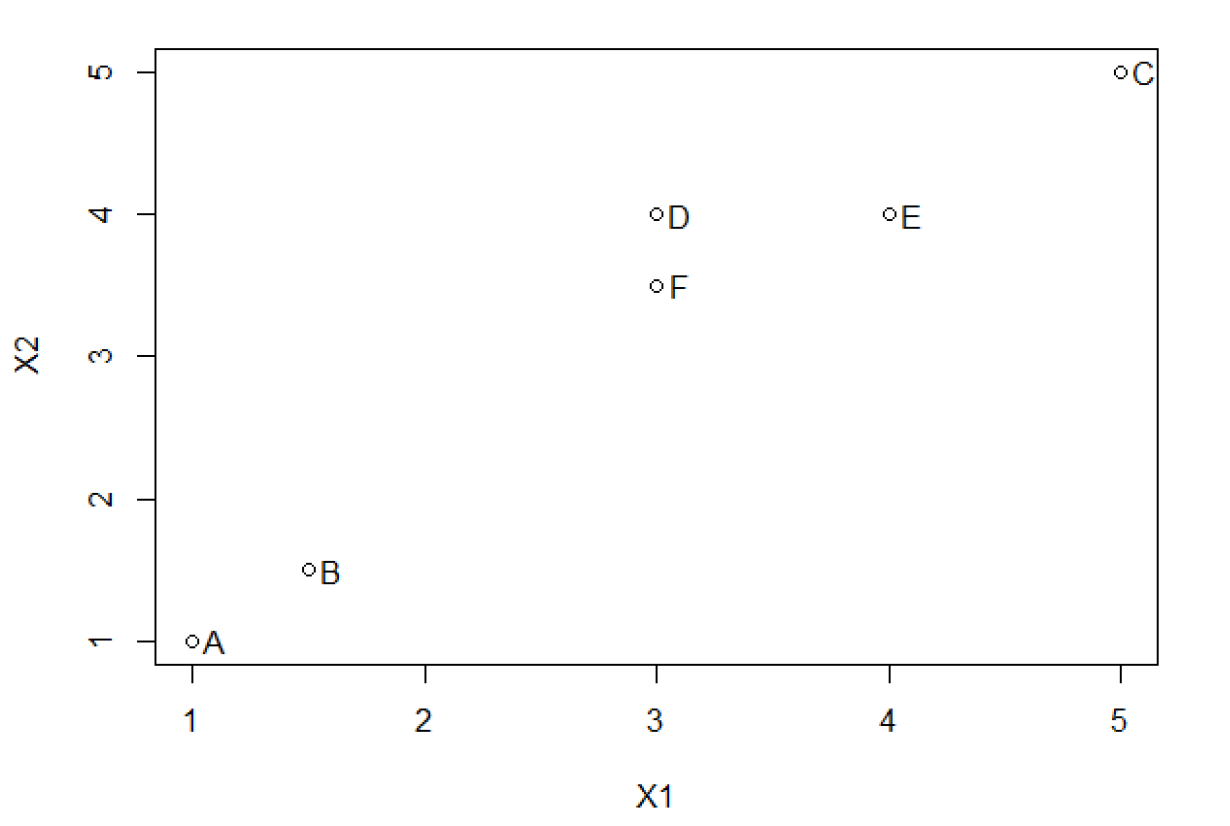
为了以图示方法演示层次聚类算法，本文引入了一个小例子。假设我们有6个对象，每个对象有两个特征，具体数据如表2所示。我们可以绘制X1与X2的散点图观察对象之间的关系，如图5所示。可以看到，A与B的距离较近，D、F、E的距离较近，C有点离群。可以通过计算样本间的距离矩阵来反应样本之间的关系。一般来说，计算距离会采用上面所说的欧氏距离。注意，距离矩阵的输出结果肯定是一个对称矩阵。这里的输出结果如表3所示。

- X1 X2
A 1.00 1.00
B 1.50 1.50
C 5.00 5.00
D 3.00 4.00
E 4.00 4.00
F 3.00 3.50
- A B C D E F
A 0.00 0.71 5.66 3.61 4.24 3.20
B 0.71 0.00 4.95 2.92 3.54 2.50
C 5.66 4.95 0.00 2.24 1.41 2.50
D 3.61 2.92 2.24 0.00 1.00 0.50
E 4.24 3.54 1.41 1.00 0.00 1.12
F 3.20 2.50 2.50 0.50 1.12 0.00

因为距离矩阵是一个对称矩阵，所以一般只采用上三角或者下三角数据，本文采用的是下三角矩阵。对角线上的元素全为0，因为计算的是样本点与自己的距离。总的来说，如果有m个样本点，那么下三角矩阵包含有\(\frac{1}{2}m(m-1)\)的数据。在我们的例子里，一共有\(1/2\times6\times(6-1)=15\)个元素。可以看出，在距离矩阵中最小的元素是0.5，即D与F之间的距离。如果样本点包含的还有分类数据，则可以采用其他方法计算样本点之间的距离。

如何将对象聚在一个类中是层次聚类的关键。给出一个距离矩阵，对象之间的距离可以通过计算类之间的距离的一些标准来确定。最基础和最常用的几个方法如下。

Single Linkageminimun distance criteron

\[d_{A\rightarrow B}=min_{\forall i \in A,\forall j \in B}(d_{ij}) \]

Complete Linkagemaximun distance criteron

\[d_{A\rightarrow B}=max_{\forall i \in A,\forall j \in B}(d_{ij}) \]

Average Groupaverage distance criteron

\[d_{A\rightarrow B}=average_{\forall i \in A,\forall j \in B}(d_{ij}) \]

Centroid distance criteron

\[d_{A\rightarrow B}=||c_A-c_B||=\frac{1}{n_in_j}\sum_ {\forall i \in A,\forall j \in B}(d_{ij}) \]

已存在的包含有\(n_k\)个样本的类k与新聚成的类\((r,s)\)之间的距离公式如下：

\[d_{k \rightarrow (r,s)} =\alpha_r d_{k\rightarrow r}+\alpha_s d_{k\rightarrow s}+\beta d_{r\rightarrow s}+ \gamma |d_{k\rightarrow r}-d_{k\rightarrow s}| \]

具体的参数如表4所示。

clustering method \(\alpha_r\) \(\alpha_s\) \(\beta\) \(\gamma\)
Single Link 1/2 1/2 0 -1/2
Complete Link 1/2 1/2 0 1/2
Unweighted pair group method average(UPGMA) \(\frac{n_r}{n_r+n_s}\) \(\frac{n_s}{n_r+n_s}\) 0 0
weighted pair group method average(WPGMA) 1/2 1/2 0 0
unweighted pair group method centroid(UPGMC) \(\frac{n_r}{n_r+n_s}\) \(\frac{n_s}{n_r+n_s}\) \(\frac{-n_sn_s}{(n_r+n_s)^2}\) 0
weighted pair group method centroid(WPGMC) 1/2 1/2 -1/4 0
Ward's method \(\frac{n_r+n_k}{n_r+n_s+n_k}\) \(\frac{n_s+n_k}{n_r+n_s+n_k}\) \(\frac{-n_k}{n_r+n_s+n_k}\) 0

最小距离层次聚类法也被称为单链聚类或者最近邻聚类。两个类之间的距离定义为两个类中对象之间距离的最小值。比如对于该例来说，最小的是D和E的距离0.50，选择先把D和E聚为一类(D,F)。然后其他单个样本之间的距离不变，计算(D,F)和其他样本之间的距离，采用最小距离法，得到的结果为：\(d((D,F),A)=d(F,A)=3.20,d((D,F),B)=d(B,D)=2.92,d((D,F),C)\)
\(=d(D,C)=2.24,d((D,F),E)=d(D,E)=1.00\),然后可以与原来的样本间距离放在一起，发现0.71——A与B之间的距离最小，因此将A与B聚为一类，得到(A,B).依次类推，最终将所有的样本点聚成一个大类。总结一下计算过程如下：

在一开始，我们有6个类，即A，B，C，D，E，F，

将距离最小为0.5的D和F聚为一类(D,F)

将距离最小为0.71的A和B聚为一类(A,B)

将距离最小为1.00的(D,F)和E聚为一类(D,F,E)

将距离最小为1.41的(D,F,E)和C聚为一类(D,F,E,C)

将距离最小为2.50的(D,F,E,C)和(A,B)聚为一类(D,F,E,C,A,B)

最后一个类包含了所有的样本点，聚类过程结束

根据上述过程，我们可以轻松的把层次聚类的树状图画出来。

那么，这个聚类的结果性能如何呢？有一个被称为共表相关系数的指标可以用来展示聚类结果的拟合优度。

为了计算层次聚类的共表相关系数，我们需要以下两个信息：

  • 距离矩阵

  • 共表矩阵

我们在上文已经计算出来了样本之间的距离矩阵，现在只需要计算共表矩阵就行了。我们需要使用在合并类的过程中使用的最小距离来填充距离矩阵的下三角。上面我们已经将合并时所使用的距离进行了总结，利用上面的总结信息，可以得到如表所示的共表矩阵。

- A B C D E F
A
B 0.71
C 2.50 2.50
D 2.50 2.50 1.41
E 2.50 2.50 1.41 1.00
F 2.50 2.50 1.41 0.50 1.00

将距离矩阵和共表矩阵一一对应生成两个向量，计算这两个向量之间的相关系数，就会得到共表相关系数。在这里，最终CPCC=86.339%,可以看到，这个聚类的效果比较好。

这里以R中自带数据集iris作为样本，使用cluster包中的hclust函数进行层次聚类，分析聚类结果。

> library(cluster)
> iris_test <- iris[,14]
> d <-dist(iris_test)
> hc1 <- hclust(d,'complete')  #最大距离法
> d1 <- cophenetic(hc1)
> cor(d,d1)
[1] 0.7269857
> 
> hc2 <- hclust(d,'single')  #最小距离法
> d2 <- cophenetic(hc2)
> cor(d,d2)
[1] 0.8638787

从上述R中的运行结果来看，single方法(最小距离法)的结果要优于complete法(最大距离法)。

聚类个数的选择

轮廓系数(Silhouette Coefficient,简称SC)

对于数据集\(x=\{x_1,x_2,...,x_n\}\),使用某种聚类方法得到类的集合\(C=\{C_1,C_2,...,C_k\}\),每个类的样本量为\(num=\{n_1,n_2,...,n_k\}\)}

\[a_i=\frac{1}{n_k-1}\sum _{x_i,x_j\in C_k}dist_{i\ne j}(x_i,x_j) \]

\[b_i=min(\frac{1}{n_l}\sum _{x_i\in C_k,x_j\in C_l,l\ne k}dist(x_i,x_j)) \]

\[S_i=\frac{b_i-a_i}{max(b_i,a_i)} \]

\[SC=\frac{1}{n}\sum _{i=1}^n S_i \]

SC即为轮廓系数。该值处于-1-1之间，值越大，表示聚类效果越好。

Gap统计量(Gap Statistic,简称GS)}

下面简单说一下Gap统计量原理及计算方法。}
Tibshirani等人在2001年提出了使用Gap统计量来确定聚类过程中最佳聚类个数k，这个统计量除了可以使用在最常用的k-means聚类方法上，对于任何聚类方法都适用。

假设有数据集\(\{x_{ij}\},i=1,2,3...,n,j=1,2,...,p\)，该数据有n个观测点和p个特征。令\(d_{ii'}\)表示观测点\(i\)和观测点\(i'\)之间的距离，最常用的是欧氏距离。

假设我们已经将数据聚成\(k\)个类，分别是\(C_1,C_2,...,C_k\)，其中\(C_r\)表示第\(r\)个类的下标，令\(n_r=|C_r|.\)即\(n_r\)表示类\(C_r\)中的观测点的个数。令

\[D_r=\sum _{i,i'\in C_r}d_{ii'}=\sum _{i,i'\in C_r}|x_i-x_i'|^2=2n_r\sum _{i\in C_r}|xi-\bar x|^2 \]

\[W_k=\sum _{r=1}^k\frac{1}{2n_r}D_r \]

也可以使用\(W_k\)来确定聚类个数\(k\)，寻找使得\(W_k\)突然变小的\(k\).但是使用\(W_k\)来确定聚类个数有以下两个问题：}

没有相关的类进行比较。
\(W_k-W_{k-1}\)的值没有进行标准化，以至于不同的模型无法进行比较。

Gap统计量将\(W_k\)进行了标准化，公式为

\[Gap_n(k)=E_n^+\{log(W_k)\}-log(W_k) , \]

寻找使得\(Gap(k)\)达到最大的那个\(k\)，即为最佳的聚类个数。
其中，\(E_n^+\)表示根据某一相关分布构造的样本量为n的数据，其
\(log(W_k)\)的期望值。
通常，构造上述的样本具有以下两种方法，即：

计算出每个特征（或变量）的取值范围，然后在该范围内随机生成n个服从均匀分布的数字，作为构造的样本观测值。
如果\(X\)是一个\(n\times p\)的数值矩阵，假设每一列的均值都是0，然后对\(X\)进行奇异值分解，

\[X=UDV^T. \]

将\(X\)进行转换，得到\(X'\)

\[X'=XV. \]

然后利用方法1根据\(X'\)得到每一列的数值\(Z'\)。
最后，将\(Z'\)进行转换，

\[Z=Z'V^T \]

最终得到我们需要的数据\(Z\)。

计算Gap统计量的步骤如下。

将数据聚类，类的个数分别取\(k=1,2,...,K\)，得出\(W_k,k=1,2,...,K.\)
根据均匀分布，使用上面的方法生成B个数据集。计算出每个数据集的
\(W_{kb}^+,b=1,2,...,B,k=1,2,...,K\)，计算出估计的Gap统计量的值：

\[Gap(k)=(1/B)\sum _b log(W_{kb}^+)-log(W_k) \]

令

\[\bar l = (1/B)\sum _b log(W_{kb}^+)$$， 计算标准误差 $$sd_k=[(1/B)\sum _b \{log(W_{kb}^+)-\bar l\}^2]^{1/2}\]

定义\(s_k=sd_k\sqrt {1+1/B}\)，最后，计算出最佳的聚类个数\(\hat k\)，

\[\hat k=smallest\ k\ such\ that\ Gap(k) \le Gap(k+1)-s_{k+1} \]

posted @ 2018-06-30 17:59  小肥羊的博客  阅读(3098)  评论(0)  编辑  收藏  举报