逻辑回归评分卡100问——基于申请评分卡

Q001、逻辑回归与线性回归的区别？

在国内的大多数金融机构内，已经很少看到使用线性回归模型来做评分卡的了。目前用的最多的还是以逻辑回归模型，当然，基于机器学习的评分模型也越来越得到市场的认可。

线性回归的一般表示方法如下：

\[p(x_i)=\beta x_i^T=\beta_0 + \beta_1x_{i1}+\beta_2x_{i2}+\cdots+\beta_nx_{in} \]

其中,\(p(x_i)\)表示在第\(i\)个样本违约的概率。

因为概率值介于0-1之间，很明显线性回归不满足这个要求。

关于逻辑回归的叙述，见我的另一篇文章《逻辑回归——牛顿法矩阵实现方式》，文中顺便给出了梯度下降求解的方法。

Q002、逻辑回归对不平衡样本是否敏感？

Q003、有哪些最优分箱的方法？

Q004、为什么需要进行WOE转换？

对于建模样本中某个特征X，假设经过WOE转换后，共计有K个分箱。即

\[W_i = ln[(N_i/\sum_{i=1}^k N_i)/(P_i/\sum_{i=1}^k P_i)] \]

现在对WoE进行改写，

\[\begin{aligned} W_i&=ln(\frac{N_i}{\sum N_i}/\frac{P_i}{\sum P_i}) \\&=ln(\frac{N_i \times (N_i+P_i)}{\sum N_i \times ( N_i+ P_i)}/\frac{P_i \times ( N_i+ P_i)}{\sum P_i \times ( N_i+ P_i)}) \\&=ln[(p_{N_i}\times\frac{ N_i+ P_i}{\sum N_i})/(P_{P_i}\times \frac{ N_i+ P_i}{\sum P_i})] \\&=ln[p_{N_i}/(1-p_{N_i}]-ln(\sum N_i/\sum P_i) \end{aligned} \]

当然，上述变式还有其他方法。根据改变后的WoE，我们可以看到，WoE与逻辑函数之间是线性关系，这就说明，经过WoE转换后的特征，特别适合用于逻辑回归模型。

另外需要说明的是，在建模样本与总体样本分布一致的情况下，根据建模样本或者总体样本计算的WoE几乎没有差别。

假设好样本是原来的10倍，坏样本样本量不变，则

\[\begin{aligned} W_i&=ln[p_{N_i^{'}}/(1-p_{N_i^{'}}]-ln(\sum N_i^{'}/\sum P_i^{'}) \\&=ln(10\times N_i/P_i)-ln(10\times \sum N_i/\sum P_i) \\&=ln[p_{N_i}/(1-p_{N_i}]-ln(\sum N_i/\sum P_i) \end{aligned} \]

但是，当某个特征在建模样本和全样本上分布差异比较大的时候，根据建模样本计算出来的WoE对于总体样本的代表性较差，此处建议根据全样本计算WoE，然后代入模型计算。

Q005、有哪些通用的数据预处理方案？

Q006、如何进行概率转评分？

逻辑回归的结果是一个类似于概率的位于(0,1)之间的实数，在实践中，我们需要将概率转化为分数。那么，到底有哪些评分转换的方式呢？

考虑下面一个简单的逻辑回归评分卡：

variable name	value	coef	woe
const.	-	-1.034	-
gender	male	0.45	0.32
gender	famale	0.45	-0.45
edu_level	高中及以下	0.86	0.54
edu_level	大专	0.86	0.05
edu_level	本科及以上	0.86	-0.61
income	(0,3000)	1.02	0.67
income	[3000,7000)	1.02	0.10
income	[7000,12000)	1.02	-0.13
income	[12000,+)	1.02	-0.44

对如下几个样本计算得分：

No.	gender	edu_level	income	constant
1	- 0.45	0.05	0.67	1
2	- 0.45	0.54	0.10	1
3	0.32	0.05	-0.13	1
4	0.32	-0.61	-0.44	1

一、直接进行线性转换

将逻辑回归的结果乘以一个固定的系数，如期望的分数区间落于(300-800)之间，并且分数越高，客户资质越好，则对应的转换公式为：

\[Score = 800 - 500\times p \]

各样本得分如下表：

No.	gender	edu_level	income	constant	Pr	score
1	- 0.45	0.05	0.67	1	0.3752	612
2	- 0.45	0.54	0.10	1	0.3385	631
3	0.32	0.05	-0.13	1	0.2730	664
4	0.32	-0.61	-0.44	1	0.1343	733

二、指定违约概率的转换

在实际业务中，我们希望客户的评分呈现正态分布，而逻辑回归的结果，是个概率值，根据逻辑函数的图像可知，概率值不可能是正态的。

另一方面，我们总是希望评分是可加的，即总分是由各个分项的子分相加得来的，概率值显然不具有这样的特性。

此外，我们还希望评分具有稳定性，即某个分数段对应的违约率应该是固定的，这样有利于风控策略的制定。同时，还要求分数每下降固定数值，违约率呈现指数递增的趋势。

也就是说，最好是评分与\(ln(odds)\)具有线性关系。

即：

\[Score = A+Bln(odds) \]

现在我们做出如下假设：

(1)500分对应好坏比为10:1

(2)评分每增加50分，好坏比增加一倍，即令PDO=50

分别将500分和550分代入上式

\[\begin{aligned} 500 &= A+ Bln(10) \\ 550 &= A +Bln(20) \end{aligned} \]

解得：

\[\begin{aligned} B&=\frac{50}{ln(2)}=72.13\\ A&=500-Bln(10)=333.9\\ \end{aligned} \]

可得评分计算公式：

\[Score =333.90+72.13ln(odds) \]

由于这里我们约定Pr是坏客户的概率，即：

\[ln(odds)=ln(\frac{Pr(G|X)}{Pr(B|X)})=ln(\frac{1-p}{p})=-ln(\frac{p}{1-p})=-(\beta_0+\beta_1x_1+\cdots+\beta_nx_n) \]

代入上述评分转换公式：

\[\begin{aligned} Score&=333.90-72.13\times(\beta_0+\beta_1x_1+\cdots+\beta_nx_n)\\ &=333.90-72.13\beta_0+72.13\times(-\beta_1x_1-\beta_2x_2-\cdots-\beta_nx_n) \end{aligned} \]

可以得到如下评分卡：

variable name	value	coef	woe	A	B	Score_Ori	Score_Adj
const.	-	-1.034	-	333.90	72.13	408	0
gender	male	0.45	0.32	333.90	72.13	-10	126
gender	famale	0.45	-0.45	333.90	72.13	15	151
edu_level	高中及以下	0.86	0.54	333.90	72.13	-33	103
edu_level	大专	0.86	0.05	333.90	72.13	-3	133
edu_level	本科及以上	0.86	-0.61	333.90	72.13	38	174
income	(0,3000)	1.02	0.67	333.90	72.13	-49	87
income	[3000,7000)	1.02	0.10	333.90	72.13	-7	129
income	[7000,12000)	1.02	-0.13	333.90	72.13	10	146
income	[12000,+)	1.02	-0.44	333.90	72.13	32	169

上述几个样本的得分如下：

No.	gender	edu_level	income	constant	Pr	score
1	- 0.45	0.05	0.67	1	0.3752	371
2	- 0.45	0.54	0.10	1	0.3385	383
3	0.32	0.05	-0.13	1	0.2730	405
4	0.32	-0.61	-0.44	1	0.1343	469

表格中，Score_Ori是计算出的原始分数，可以看出分数有正有负。一个比较合理的调整方案是，将常数项的分数，平均分配到每个得分中。这里一共有3个变量，则将408均分到三个变量上，使每个变量都变成正数。

全为正数的得分更加符合人的逻辑，同时也方便部署。

三、指定分数区间的转换

第二种转换方式，得到的评分区间不总是固定的，如果想要评分固定在某个区间内，则可以稍作调整。

已知变量取值经过WoE转换以后，值是有限的，因此，得到的评分，也一定是有限的。我们假设评分介于300-850之间，即

\[\begin{aligned} Score_{min}=A+B\times min(ln(odds))=300\\ Score_{max}=A+B\times max(ln(odds))=850 \end{aligned} \]

根据上一节可知：

\[ln(odds)=-(\beta_0+\beta_1x_1+\cdots+\beta_nx_n) \]

则：

\[\begin{aligned} min(ln(odds))&=min(-(\beta_0+\beta_1x_1+\cdots+\beta_nx_n))\\ &=-(-1.034+0.32\times0.45+0.54\times0.86+0.67\times1.02)\\ &=-0.2578 \end{aligned} \]

同理，

\[\begin{aligned} max(ln(odds))&=max(-(\beta_0+\beta_1x_1+\cdots+\beta_nx_n))\\ &=2.2099 \end{aligned} \]

代入评分转换公式：

\[\begin{aligned} Score_{min}&=A+B\times (-0.2578))=300\\ Score_{max}&=A+B\times 2.2099=850 \end{aligned} \]

解得：

\[\begin{aligned} A&=357.46\\ B&=222.88\\ Score&=357.46+222.88ln(odds)\\ &=357.46-222.88\times(\beta_0+\beta_1x_1+\cdots+\beta_nx_n) \end{aligned} \]

可以得到如下评分卡：

variable name	value	coef	woe	A	B	Score_Ori	Score_Adj
const.	-	-1.034	-	347.46	222.88	588	0
gender	male	0.45	0.32	347.46	222.88	-32	164
gender	famale	0.45	-0.45	347.46	222.88	46	242
edu_level	高中及以下	0.86	0.54	347.46	222.88	-105	91
edu_level	大专	0.86	0.05	347.46	222.88	-10	186
edu_level	本科及以上	0.86	-0.61	347.46	222.88	120	316
income	(0,3000)	1.02	0.67	347.46	222.88	-156	40
income	[3000,7000)	1.02	0.10	347.46	222.88	-23	173
income	[7000,12000)	1.02	-0.13	347.46	222.88	31	227
income	[12000,+)	1.02	-0.44	347.46	222.88	104	300

上述几个样本的得分如下：

No.	gender	edu_level	income	constant	Pr	score
1	- 0.45	0.05	0.67	1	0.3752	471
2	- 0.45	0.54	0.10	1	0.3385	507
3	0.32	0.05	-0.13	1	0.2730	578
4	0.32	-0.61	-0.44	1	0.1343	778

四、总结

上述三种方法，均是比较常用的评分转换方式。其中，方法二和方法三比较常用于信用分的转换，方法一常用于欺诈分的转换。上述几个方法各有优劣，主要表现为：

(1)方法一直接使用概率的线性转换，简单明了，但是转换后的分数不符合正态分布，会在高分段大规模集中，不符合业务上的直觉。

(2)方法二是目前最常用的转换方式，对于采用同一基准和PDO的分数，可以直接进行对比。但是方法二无法保证评分落在某个固定区间。

(3)方法三保证了评分介于一个固定的区间，但是模型迭代以后，相同评分对应的违约率不同，相应的策略可能需要调整。

值得说明的是，上述三种方法，评分的排序是一致的，即评分在总体中的位置是不变的。

综上，本文建议使用方法二。

Q007、如何评价评分卡好坏？

All models are wrong, but some are useful.
——George E. P. Box

正如英国统计学家George E. P. Box所言，所有的模型都是错误的，但有一些很有用。这句话，用在信用评分领域最好不过了。对于信用评分的开发者来说，我们的目的不是找一个预测率百分比的模型，当然，这样的模型也找不到。而是找一个有用的模型，能够有效的区分出高风险客群和低风险客群。银行等金融机构就是经营风险的，在平衡风险的过程中获利。

那么，什么样的模型才是有用的模型呢？

在实践中，我们经常使用KS统计量来衡量模型的区分度，并且总是以自己的KS高于竞争对手而感到自豪。KS统计量是基于经验累积概率分布函数计算出来的，在同一个图中，绘制出好客户和坏客户的经验累积概率分布函数，两条曲线之间的最大差值，即是KS统计量。

上述为某机构申请评分模型的全样本KS表现，在580-600这个分数区间内，KS达到最大值60%。在实践中，很多同学对于KS抱有疑问，主要表现为以下几点：

(1)cut-off是否应该切在KS所在区间？

(2)KS是否越大越好？

下面，我们一个一个来解答。

对于问题一，KS是用来衡量模型的最大区分能力，而具体cut-off的确定，还需要策略的同学进行分析后确定。在进行cut-off确定的时候，我们要同时考虑核准率和不良率，并且辅之以提升度进行分析确定。

评分	全样本	好	坏	累积全样本	累积好	累积坏	好占比	坏占比	好累积	坏累积	KS	Bad_Rate	ln(odds)	Bad_Rate2	Bad_Rate3	Lift	核准率
[300, 320)	18	6	12	18	6	12	0.01%	0.40%	0.01%	0.40%	0.40%	66.67%	-0.69	66.67%	2.92%	22.73	99.98%
[320, 340)	52	23	29	70	29	41	0.02%	0.97%	0.03%	1.38%	1.35%	55.77%	-0.23	58.57%	2.89%	19.97	99.93%
[340, 360)	76	32	44	146	61	85	0.03%	1.48%	0.06%	2.85%	2.79%	57.89%	-0.32	58.22%	2.85%	19.85	99.86%
[360, 380)	144	61	83	290	122	168	0.06%	2.79%	0.12%	5.64%	5.52%	57.64%	-0.31	57.93%	2.78%	19.75	99.71%
[380, 400)	200	108	92	490	230	260	0.11%	3.09%	0.23%	8.73%	8.50%	46.00%	0.16	53.06%	2.69%	18.09	99.52%
[400, 420)	346	212	134	836	442	394	0.22%	4.50%	0.45%	13.23%	12.78%	38.73%	0.46	47.13%	2.57%	16.07	99.18%
[420, 440)	513	342	171	1349	784	565	0.35%	5.74%	0.80%	18.97%	18.18%	33.33%	0.69	41.88%	2.41%	14.28	98.67%
[440, 460)	786	594	192	2135	1378	757	0.60%	6.45%	1.40%	25.42%	24.02%	24.43%	1.13	35.46%	2.23%	12.09	97.90%
[460, 480)	1086	849	237	3221	2227	994	0.86%	7.96%	2.26%	33.38%	31.12%	21.82%	1.28	30.86%	2.02%	10.52	96.83%
[480, 500)	1472	1236	236	4693	3463	1230	1.25%	7.92%	3.51%	41.30%	37.79%	16.03%	1.66	26.21%	1.80%	8.94	95.38%
[500, 520)	2104	1842	262	6797	5305	1492	1.87%	8.80%	5.38%	50.10%	44.72%	12.45%	1.95	21.95%	1.57%	7.48	93.31%
[520, 540)	2807	2547	260	9604	7852	1752	2.58%	8.73%	7.97%	58.83%	50.86%	9.26%	2.28	18.24%	1.33%	6.22	90.54%
[540, 560)	3621	3370	251	13225	11222	2003	3.42%	8.43%	11.39%	67.26%	55.87%	6.93%	2.60	15.15%	1.10%	5.16	86.98%
[560, 580)	4535	4300	235	17760	15522	2238	4.36%	7.89%	15.75%	75.15%	59.40%	5.18%	2.91	12.60%	0.88%	4.30	82.51%
[580, 600)	5482	5297	185	23242	20819	2423	5.37%	6.21%	21.12%	81.36%	60.24%	3.37%	3.35	10.43%	0.71%	3.55	77.11%
[600, 620)	6319	6172	147	29561	26991	2570	6.26%	4.94%	27.38%	86.30%	58.92%	2.33%	3.74	8.69%	0.57%	2.96	70.89%
[620, 640)	7150	7021	129	36711	34012	2699	7.12%	4.33%	34.51%	90.63%	56.12%	1.80%	4.00	7.35%	0.43%	2.51	63.85%
[640, 660)	7740	7657	83	44451	41669	2782	7.77%	2.79%	42.28%	93.42%	51.14%	1.07%	4.52	6.26%	0.34%	2.13	56.22%
[660, 680)	8112	8044	68	52563	49713	2850	8.16%	2.28%	50.44%	95.70%	45.26%	0.84%	4.77	5.42%	0.26%	1.85	48.23%
[680, 700)	8043	7999	44	60606	57712	2894	8.12%	1.48%	58.55%	97.18%	38.63%	0.55%	5.20	4.78%	0.21%	1.63	40.31%
[700, 720)	7469	7435	34	68075	65147	2928	7.54%	1.14%	66.10%	98.32%	32.22%	0.46%	5.39	4.30%	0.15%	1.47	32.96%
[720, 740)	7048	7035	13	75123	72182	2941	7.14%	0.44%	73.23%	98.76%	25.52%	0.18%	6.29	3.91%	0.14%	1.33	26.02%
[740, 760)	6269	6256	13	81392	78438	2954	6.35%	0.44%	79.58%	99.19%	19.61%	0.21%	6.18	3.63%	0.12%	1.24	19.84%
[760, 780)	5382	5370	12	86774	83808	2966	5.45%	0.40%	85.03%	99.60%	14.57%	0.22%	6.10	3.42%	0.08%	1.17	14.54%
[780, 800)	4491	4487	4	91265	88295	2970	4.55%	0.13%	89.58%	99.73%	10.15%	0.09%	7.02	3.25%	0.08%	1.11	10.12%
[800, 820)	3579	3576	3	94844	91871	2973	3.63%	0.10%	93.21%	99.83%	6.62%	0.08%	7.08	3.13%	0.07%	1.07	6.60%
[820, 840)	2640	2639	1	97484	94510	2974	2.68%	0.03%	95.89%	99.87%	3.98%	0.04%	7.88	3.05%	0.10%	1.04	4.00%
[840, 860)	1870	1868	2	99354	96378	2976	1.90%	0.07%	97.78%	99.93%	2.15%	0.11%	6.84	3.00%	0.09%	1.02	2.15%
[860, 880)	1295	1294	1	100649	97672	2977	1.31%	0.03%	99.10%	99.97%	0.87%	0.08%	7.17	2.96%	0.11%	1.01	0.88%
[880, 900)	892	891	1	101541	98563	2978	0.90%	0.03%	100.00%	100.00%	0.00%	0.11%	6.79	2.93%	0.00%	1.00	0.00%
合计	101541	98563	2978	101541	98563	2978	100%	100%	-	-	60%	2.93%	3.50	-		-	-

上表为各个分数区间的指标统计。如果在KS最大处拒绝，此时的核准率为77.11%，拒绝样本违约率为10.43%，通过样本的违约率为0.71%。相比于不使用评分卡时的违约率2.93%，使用评分卡后违约率大幅降低。

但是需要注意的是，金融机构的最终目标是收益，如果不良率在可控范围内，可以适当提高风险容忍度。比如此时把540分以下的拒绝，此时的核准率为90.54%，那么拒绝样本的违约率为18.24%，通过样本的违约率为1.33%。相对于不使用评分卡，违约率降低了一半以上，而通过客户数却没有显著的损耗。

我们还可以根据提升度进行cut-off切分，比如Lift大于6的客群，全部拒绝，此时拒绝线在540分；Lift介于2-6之间的转人工或者走其他通道复核，那么540-660分之间的客户可以这样处理；对于Lift小于2的客群，可以直接通过，此时区间内的违约率已经降至1%以内，远低于2.93%的平均违约率。

单从风险的角度进行切分是不全面的，必要的时候，还可以结合收益测算，划分最佳切分点。

针对问题二，在一定范围内，KS越大越好，但是一般KS不宜超过70%。否则一方面模型可能有点问题，另一方面，不利于cut-off的确定。

下面，我们绘制出好客户和坏客户的概率密度函数。

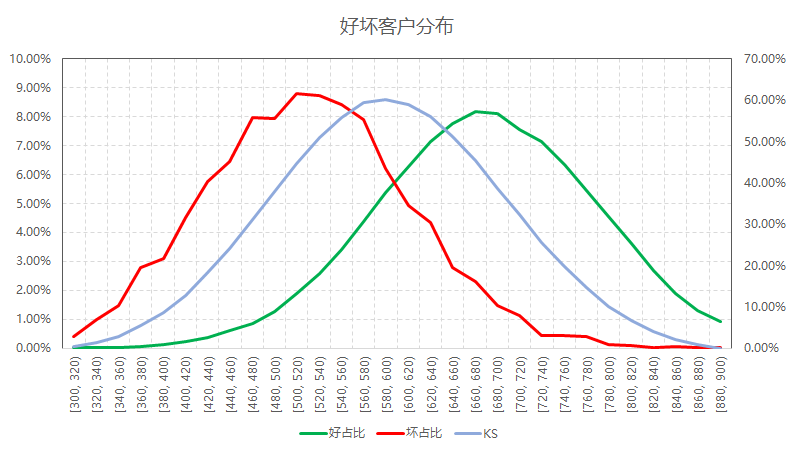
从上图可以看出，此评分不仅具有较高的KS，而且好坏样本十分接近正态分布，从统计的角度而言，该模型表现优异。

图中KS曲线的极值点落在好坏客户的概率密度曲线交叉的地方。在极值点左边，坏客户的概率密度总是高于好客户的，因此KS曲线不断上升。在极值点右边，坏客户的概率密度低于好客户，KS逐渐下降。因此，如果要KS达到较大的值，需要将两个概率密度曲线的交点向下压。这就意味着，好坏客户的分布，偏度会增大，而不是接近于正态分布了。

Q008、IV值可以怎么理解？

IV，翻译成中文即是信息值，其原理即KL散度，在信息论中，用来描述两个概率分布P和Q的差异。在信用评分领域，IV值的计算公式为：

\[IV=\sum_{i=1}^n(\frac{N_i}{\sum N}-\frac{P_i}{\sum P})\times WoE_i \]

IV值总是正的。对于变量\(x_i\)的各个区间，如果该区间内好客户与所有好客户的占比等于坏客户与所有坏客户的占比相等，则说明对于\(x_i\)的不同取值，好坏客户的分布没有差异，那么，该变量对于区分好坏客户没有任何价值。从这个角度来看，IV值越大越好。

在极端情况下，IV值可能大于3，大于2的IV已经非常少见，IV大于1的变量一般是具有较强预测能力的变量。

一般来说，分箱越多，IV越高，本文不建议通过以划分较多的区间而获得较大IV的方式。在建模时，如果一开始加入IV较大的变量，则后续很多变量可能无法进入。此处的建议是，先让IV很大的变量放在一边，在后面进入模型。

变量的IV是一种横向比较，即在同一时刻，比较好坏客户的分布是否具有显著差异。那么，纵向来看，IV值还可以用来衡量当前客群分布于未来时点客群分布的区别，即我们常说的PSI。

对于单变量，我们还可以根据相同的理论，计算出单变量的稳定性指标。

Q009、评分卡对回归系数有要求吗？

一、回归系数应通过\(Wald\)检验

二、除常数项外，回归系数同号

三、回归系数绝对值不应太小

Q010、什么是逻辑回归的正则化？