算法篇【递归2 -- N皇后问题】

问题：输入整数N，要求在N*N的棋盘上，互相不能攻击，不在同一行同一列上，切不在对角线上，输出全部方案。

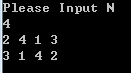
输入：

         4

输出：

         2  4  1  3

         3  1  4  2

思路：

         假设在前k-1个摆好的条件下，求出第k个皇后的摆法，并保存，继续求第k+1个皇后的摆法，直到找到合适的摆法。

 

#include <iostream>
#include <cmath>
using namespace std;
int  N ;
int  queenPos[100] ;
//用来存放算好的皇后的位置，比如第1行皇后在第i列，则queenPos[0]=i; 第2行皇后在第j列，则queenPos[1]=j;依次输出所有n行皇后的位置
void NQueen(int k);
//NQueen(k) 表示前k-1个皇后都摆好的情况下，第k个皇后的摆法。

int main(){
    cout << "Please Input N " << endl;
    cin >> N  ;
    NQueen(0) ;//从第0行开始摆皇后 ，直到摆好N行 
    return 0  ;
    system("pause");
}

void NQueen(int k){
    int  i ;
    if(k==N){
        //递归函数的结束条件。从第1个皇后到第N个皇后都已经摆好了
        for(int i=0; i<N; i++){
            cout << queenPos[i] + 1 << " ";
        } 
        cout << endl;
        return ;
    }
    
    //该for循环用来尝试第k个皇后的位置 ，位置为变量i 
    for(int i=0; i<N; i++){
        int j ;
        //变量j的循环用来判断第k个皇后放在位置i列处，是否和已经摆好的k-1个皇后的列位置queenPos[j]冲突 
        for(j=0; j<k; j++){
            if(queenPos[j] == i ||//第k个皇后摆在第i列和已经摆放的皇后列位置有相同的。 
                abs(queenPos[j]-i) == abs(k-j)//列的绝对值只差==行的绝对值只差，k-j中的k表示第k个皇后在第k行，循环变量j表示的是已经摆好的行数下标。 
              ) 
                break ; 
        }
        if(j==k){//前面j的for循环没有break，则表示当前第k行的位置i不冲突，则保存该值，并在此基础上求下一行皇后的摆放位置 
            queenPos[k] = i;
            NQueen(k+1);//首先会判断新的k是否==N，是的话，则输出摆放位置 ，return到NQueen[N-1],...直到返回NQueen【0】，main函数执行return 0. 
        }
    }
    //假设N=4，由于求NQueen（0）时，第一个皇后的位置是2，此时在for（int i=0; i<N; i++）。的循环中，成功return 之后返回到for 循环中，重新计算出下一个合理摆法 
}