算法篇【递归1 -- 汉诺塔问题】

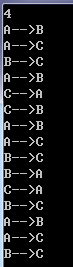
问题：A,B,C 三个塔座，A上有64个盘子，盘子大小不等，大的在下，小的在上，现在想要把64个盘子从A座上移动到C座，但是每次只能移动一个盘子，且每个塔座上始终要保持大盘在下，小盘在上，求出移动步骤。

输入：

         第一行是一个正整数，表示有多少个盘子

输出：

         每一次是如何移动盘子的，

思路：

         刚开始的时候，首先需要将N个盘子的前N-1个移动到中转塔上，然后将第N个盘子从src塔上移动到dst塔上，将前N-1个移动到中转塔上的问题，就是分解后N-1个盘子的Hanoi塔问题。然后对N-1个盘子的Hanoi塔问题再进行求解。

 

#include <iostream>
using namespace std;

void Hanoi(int n, char src, char mid, char dst){
    //将src上的n个盘子，以mid为中转，移动到dst上。 
    if(n==1){
        //只需要移动一个盘子时，直接将盘子从src移动到dst即可。 
        cout << src << "-->" << dst << endl;
        return; 
    }
    //先将n-1个盘子从src移动到dst。 
     Hanoi(n-1, src, dst, mid);
     //再将一个盘子从src移动到dst。 
     cout << src << "-->" << dst << endl;
     //递归算法，最后将n-1个盘子从mid移动到dst。 
     Hanoi(n-1, mid, src, dst);
     return;
}
 
int main()
{
    int n ;
    cin >> n ;
    Hanoi(n, 'A', 'B', 'C') ;
    return 0;
    system("pause");
}