线段树优化建图

分为四种操作：

1. 单点向单点连边

2. 单点向区间连边

3. 区间向单点连边

4. 区间向区间连边

1可以和其他几个合并

接下来讲实现。

我们考虑用两棵线段树来搞，建两棵线段树，一棵处理入边，一棵处理出边，方便起见，我们下文称其为入树和出树。

开始我们让父亲和儿子连边，然后我们再让入树和出树的叶子节点之间连上边权为0的边。

建出来的图和下图一样，盗图

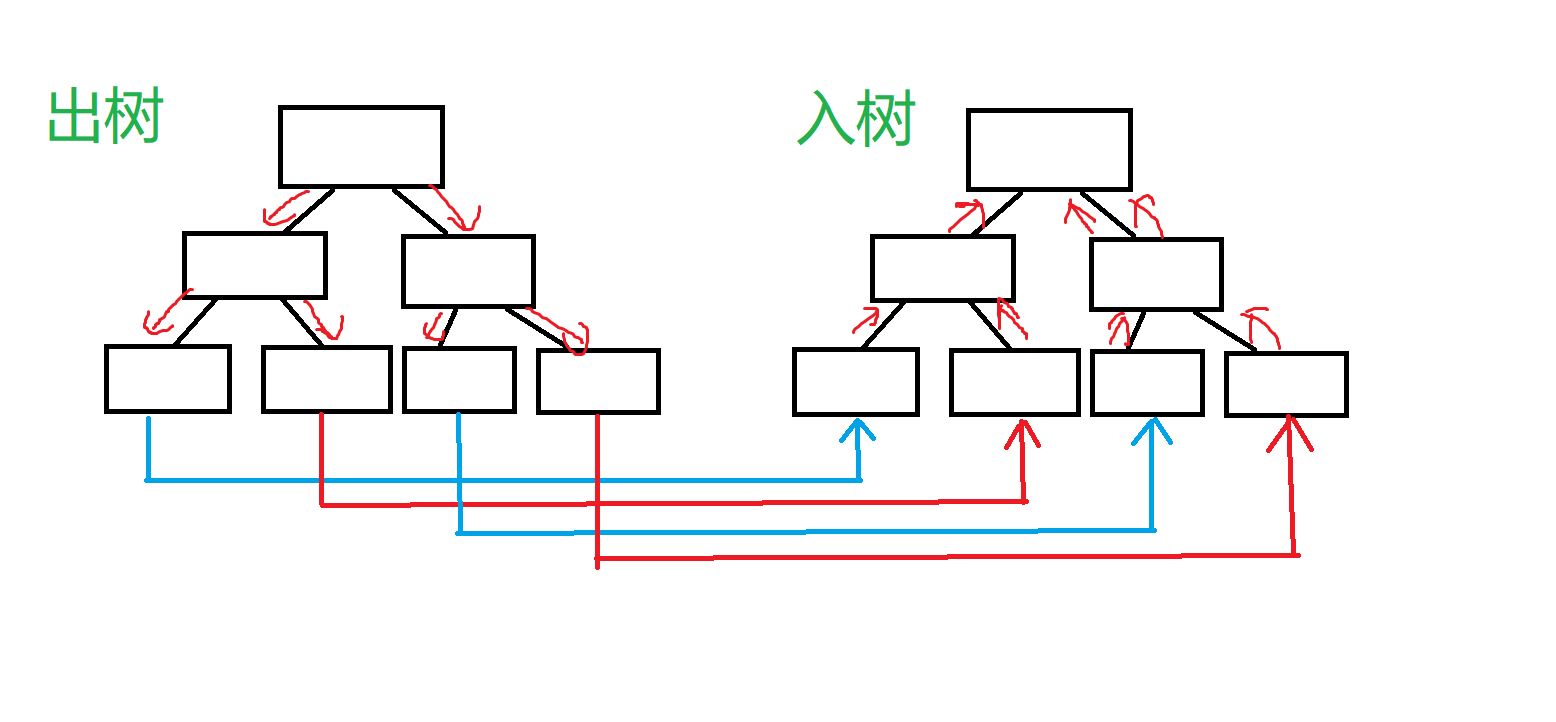
这部分代码：op = 1建的是入树，否则为出树

void build(int &x,int l,int r,int op){
	if (l == r){x = l;return;}
	x = ++tot;
	int mid = (l+r >> 1);
	build(ls[x],l,mid,op),build(rs[x],mid+1,r,op);
	if (op == 1) add(x,ls[x],0),add(x,rs[x],0);
	if (op == 2) add(ls[x],x,0),add(rs[x],x,0);
}

现在我们需要用modify操作来单点像连边。

我们首先定义修改区间为[L,R]，我们有两种操作。

类似区间修改操作，如果当前区间被[L,R]涵盖，我们就连边。

注意根据操作要求连边，不要连反了。

void modify(int x,int l,int r,int nl,int nr,int p,int w,int op){
//	cout<<op<<endl;
	if (nl <= l&&r <= nr){
		if (op == 2) add(p,x,w);
		if (op == 3) add(x,p,w);
		return;
	}
	int mid = (l+r >> 1);
	if (nl <= mid) modify(ls[x],l,mid,nl,nr,p,w,op);
	if (nr > mid) modify(rs[x],mid+1,r,nl,nr,p,w,op);
}

最后是区间向区间连边，每次建一个虚点然后连边就好了

void modify(int x,int l,int r,int nl,int nr,int op){
	if (nl <= l&&r <= nr){
		if (op == 1) add(x,tot,1);
		if (op == 2) add(tot,x,1);
		return;
	}
	int mid = (l+r >> 1);
	if (nl <= mid) modify(ls[x],l,mid,nl,nr,op);
	if (nr > mid) modify(rs[x],mid+1,r,nl,nr,op);
}