扩展KMP详解

最近新学的三个算法，一直都没写博客，后缀自动机和线性基还有一点小尾巴，争取这两天结束

一、应用场景

求\(T\)串与\(S\)串的每个后缀的最长公共前缀

二、算法流程

图片来源

1. 假设当前遍历到S串位置i，即nxtS[0]...nxtS[i - 1]这i个位置的值已经计算得到。设置两个变量，st和pos。pos代表以st为起始位置的字符匹配成功的最右边界，也就是"pos = 最后一个匹配成功位置"。相较于字符串T得出，S[st...pos]等于T[0...pos-st]。

2. 再定义一个辅助数组int nxtT[]，其中nxtT[i]含义为：T[i]...T[m - 1]与T的最长相同前缀长度

3. 根据第一条得出：S[i]对应T[i - st]，S[i...pos] = T[i - st...pos - st]，同时我们已经知道T[i - st...]与T的最长公共前缀，而T[i - st...pos - st]的最长公共前缀一定比它小，所以如果i + nxtT[i - st] < pos，说明最长公共前缀在我已知的范围内，根据nxtT数组的定义，此时nxtS[i] = nxtT[i - st]。

4. 如果i + next[i - st] == pos呢？S[pos+1] != T[pos - st + 1]且T[pos - i + 1] != T[pos - st + 1]，但S[pos]有可能等于T[pos - i + 1]，所以我们可以直接从S[pos + 1]与T[pos - i + 1]开始往后匹配，加快了速度。

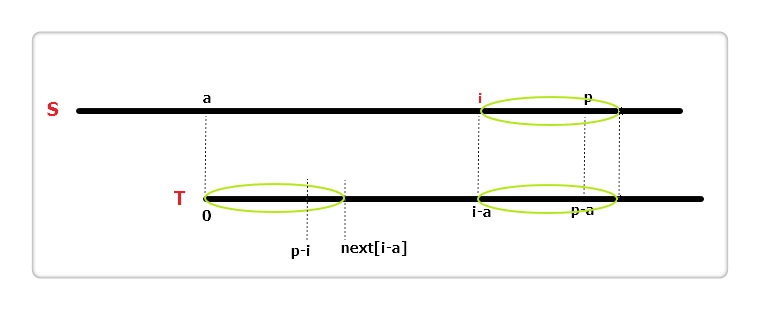
5. 如果i + nxtT[i - st] > pos呢？那说明S[i...pos]与T[i-st...pos-st]相同，注意到S[pos + 1] != T[pos - st + 1]且T[pos - i + 1] == T[pos - st + 1]，也就是说S[pos + 1] != T[pos - i + 1]，所以就没有继续往下判断的必要了，我们可以直接将nxtS[i]赋值为pos - i + 1。

明天更……

三、代码

1. 第一次扩展

    for (int i = 0;S[i] == T[i]&&i < lenT&&i < lenS;i++) pos++,nextS[0]++;

2. 4和5两条可以合并

 if (nextT[i-st] >= pos-i+1){
            int j = max(pos-i+1,0);
            while(S[i+j] == T[j]&&i+j < lenS&&j < lenT) j++;
            nextS[i] = j,st = i;
 }

3. 第3条

else nextS[i] = nextT[i-st];

完整代码：因为我需要先求一个nxtT，所以需要调用两边函数

        for (int i = 2,l = 1,r = 1;i <= lenb;i++){
		if (i <= r&&kmpA[i-l+1] < r-i+1) kmpA[i] = kmpA[i-l+1];
		else{
			kmpA[i] = max(0,r-i+1);
			while (i+kmpA[i] <= lenb&&b[kmpA[i]+1] == b[i+kmpA[i]]) ++kmpA[i];
		}
		if (i+kmpA[i]-1 > r) l = i,r = i+kmpA[i]-1;
	}
	for (int i = 1,l = 0,r = 0;i <= lena;i++){
		if (i <= r&&kmpA[i-l+1] < r-i+1) kmpB[i] = kmpA[i-l+1];
		else{
			kmpB[i] = max(0,r-i+1);
			while (i+kmpB[i] <= lena&&b[kmpB[i]+1] == a[i+kmpB[i]]) ++kmpB[i];
		}
		if (i+kmpB[i]-1 > r) l = i,r = i+kmpB[i]-1;
	}