四则运算开平方——对民科吧编程大赛题目的再探究

题目传送地址：https://tieba.baidu.com/p/6809881927

规则大意：
仅仅使用加减乘除四则运算进行任意正数的算数平方根运算
可以多次迭代
精度要求到小数点后的6位

解答部分：

前言：

几乎是很迅速地，我能想到四种方法（这四种方法都是高等数学书上列出的）：

二分迭代法，牛顿迭代法，拟牛顿迭代法，弦截迭代法。

经过深入思考以后我想到了另外两种速度比较快的算法：

导数迭代法，向量趋近迭代法（自己想的瞎起的名）。

 2020.7.22 今天先写一下导数迭代法。

导数迭代法：

求一个方程 $f(x)=a$ 的解。

由导数的定义可知，如果把 $x$ 加上一个很小的值 $\Delta x \to 0$，那么$f(x+ \Delta x)$就变成了$f(x)+f'(x) \bullet \Delta x$。

由此我们可以先求出$f(x)$的一个近似解 $x_0$作为初始迭代值。每次增加$\Delta x = \dfrac{(f(x_i) - a)}{f'(x_i)}$

因为$\Delta x$ 的值很小，每迭代一次就会离最终结果更近一点。经过反复迭代以后就可以达到足够的精度。

此方法对于任意平滑函数求解方程的根都可适用。

归纳步骤：

对一个数 $a$ 求平方根，就是求 $a^{\frac{1}{2}}$ 的值。

令$f(x)=\sqrt{x}$，则$f'(x)=-\dfrac{1}{2 \sqrt{x}}$

我们可以先求出$f(x) =a$的一个近似解，可以选择$a$的数量级的一半（语文不好，即 $x_0 = 10^{\left \lfloor \frac{ \lg (a) }{2}\right \rfloor}$）作为初始迭代值。

可以发现$f'(x)$中仍然出现了开方。由于我们无法使用开平方函数，所以在计算过程中不能使用普通的导数迭代法，要重新构建模型：

我们可以确定的是$\sqrt{1}=1$，那么为什么不用$1$作为函数的近似解呢？

不要以为我在异想天开！将$x=1$带人以后就可以得到：

 

$\lim \limits_{\Delta x \to 0} \sqrt{1+\Delta x} = 1+\frac{x}{2}$

我们假设已经求出来了方程$f(x) =a$的一个近似解$x_0$，那么就有：

$a= \sqrt{x_0^2+ \Delta x}$

提出来一个$x_0$以后就变成了：

$a= x_0  \sqrt{1+ \dfrac{\Delta x}{x_0^2}}$

很成功地，我们得到了下一个迭代近似解$x_1$：

$x_1= x_0  (1+ \dfrac{\Delta x}{2x_0^2})$

即：

$x_1= x_0 +  \dfrac{\Delta x}{2x_0}$

来进行下一次迭代。

 

代码实现：

由于博主水平有限，到目前为止只会 C++ （倒是学过一点 Python 但是现在都忘了），抱歉只能写一个残废的代码（不支持高精度，卡不卡炸不炸只能看您的数据和电脑配置）。

 

 1 #include<bits/stdc++.h>
 2 using namespace std;
long double a,b,c;
int w,ite,i=1;
int get_lg(int m){
    while(m)w++,m/=10;
    return w;
}
int get_first_ite(int m){
    while(m)m--,i*=10;
    return i;
}
int main(){
    cin>>a;
    b=get_first_ite(get_lg(a)/2);
    while(abs(b*b-a)>1e-6){
        ite++;
        c=b*b-a;
        b-=(c/(2*b));
        cout<<"iterate time="<<ite<<"  b="<<b<<"  error="<<abs(b*b-a)<<endl;
    }
    cout<<fixed<<setprecision(6)<<b<<endl;
}

 

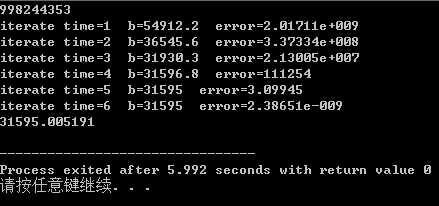
可以发现此方法的迭代次数还是很少的

__EOF__

本文作者：小红
本文链接：https://www.cnblogs.com/little-red/p/Iterate_sqrt.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！