民科吧编程赛 试题
1.选择题
【题目要求】
只允许使用四则运算,求出任意正数 的自然对数
【输入】
一个数
【输出】
一个数 保留 6 位小数。
【时空限制】
2.填空题
【题目要求】
本题允许使用四则运算和函数,给出两个数,求在区间的最大值。其中
由于今天小红比较开心,所以特地帮你们把这个函数的导函数求了出来:
(懒得打公式了,就这么着看)
【输入】
两个数
【输出】
一个数,保留6位小数。
【时空限制】
3.解答题(物理向)
【题目要求】
平面直角坐标系中有个质点,给出各质点的坐标与质量,求它们质心的坐标。
本题不会编程的可手算,保留一位小数即可。
此题允许使用四则运算和函数
【输入】
第一行一个数,表示个质点。
第行三个数,表示各个质点的坐标和质量。
【输出】
两个数,保留3位小数。
【时空限制】
【评分细则】
令标准答案为,你的答案为:
得分
(对于手算,得分)
__EOF__

本文作者:小红
本文链接:https://www.cnblogs.com/little-red/p/13385463.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!
本文链接:https://www.cnblogs.com/little-red/p/13385463.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!

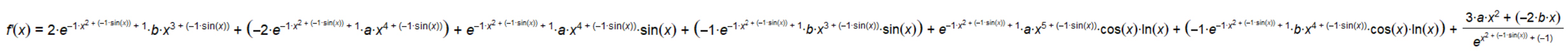


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)