引入语义标签过滤:利用标签相似度增强检索
引入语义标签过滤:利用标签相似度
增强检索
传统的标签搜索缺乏灵活性。如果我们要过滤恰好包含给定标签的样本,可能会出现这样的情况,特别是对于只包含几千个样本的数据库,
可能没有任何(或只有少数)与我们的查询匹配的样本。
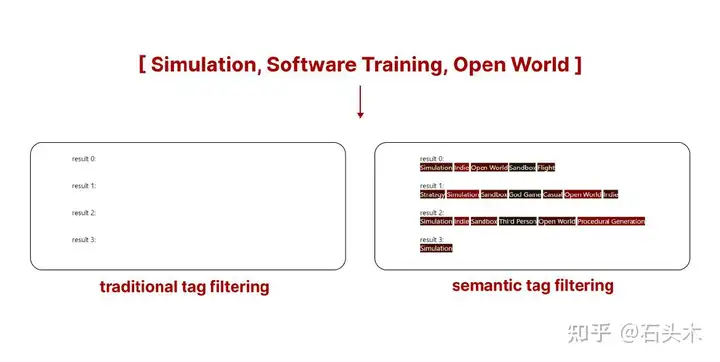
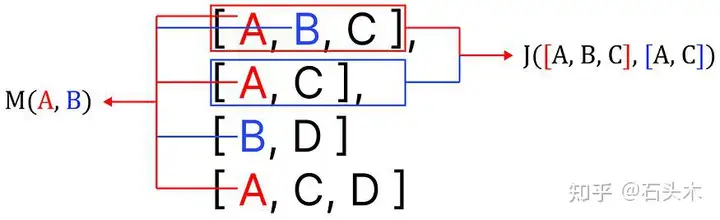
两种搜索的不同之处在于搜索结果的稀缺性
传统的标签搜索是如何工作的?
传统系统采用一种称为 Jaccard 相似性的算法(通常通过 minhash 算法执行),该算法能够计算两组元素之间的相似性(在我们的示例中,这些元素是标记)。如前所述,搜索一点也不灵活(集合要么包含,要么不包含查询的标签)。
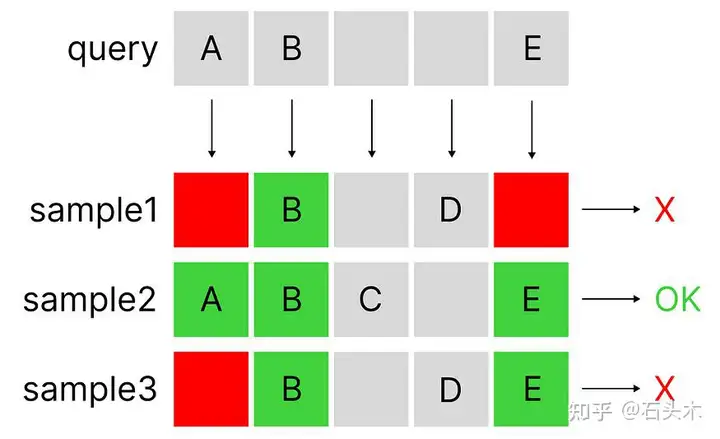
一个简单的 AND 位操作的例子(这不是 Jaccard 相似,但可以是一个近似的过滤方法的想法)
是否能做得更好?
相反,如果我们不只是从匹配的标签中过滤样本,而是考虑样本中所有不相同但与我们选择的标签相似的其他标签,会怎么样?我们可以使算法更加灵活,将结果扩展到非完美匹配,但仍然是好的匹配。我们将直接将语义相似性应用于标签,而不是文本。
语义标签搜索
如前所述,这种新方法试图将语义搜索的功能与标签过滤系统相结合。要构建这个算法,我们只需要做一件事:
- 一个标记样本的数据库
这里使用参考数据是 Steam 游戏库的开源集合(可从 Kaggle )-大约40,000 个样本,这是一个很好的样本量来测试我们的算法。从显示的数据框中我们可以看到,每个游戏都有几个分配的标签,在我们的数据库中有超过 400 个唯一的标签。
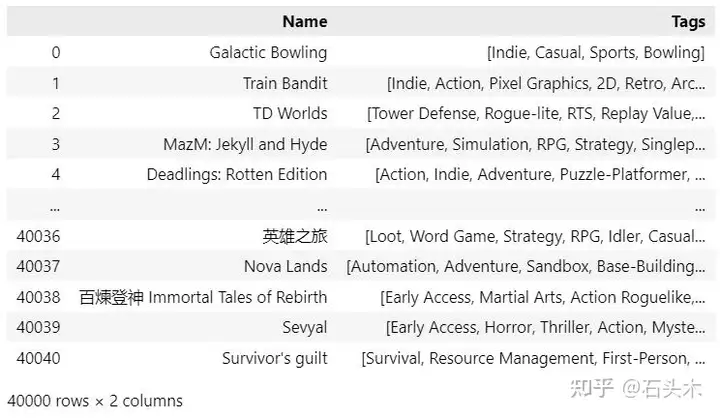
现在有了原始数据,我们可以继续,算法处理步骤如下:
- 提取标签关系
- 编码查询和样本
- 使用向量检索执行语义标签搜索
- 验证
本文只探讨这种新方法背后的数学原理。
1.提取标签关系
想到的第一个问题是我们如何找到标签之间的关系。请注意,有几种算法用于获得相同的结果:
- 使用统计方法
我们可以用来提取标签关系的最简单的可使用方法被称为共现矩阵。
- 使用深度学习
最先进的都是基于 Embeddings 神经网络(比如过去的 Word2Vec,现在常用的是使用transformers,比如 llm),可以提取样本之间的语义关系。创建一个神经网络来提取标签关系(以自动编码器的形式)是一种可能性,在面对某些情况时通常是可取的。
- 使用预训练模型
因为标签是使用人类语言定义的,所以可以使用现有的预训练模型来计算已经存在的相似度。这可能会快得多,也不那么麻烦。然而,每个数据集都有其独特性。使用预训练的模型会忽略客户的行为。
算法的选择可能取决于很多因素,特别是当我们必须处理一个巨大的数据池或者我们有可扩展性问题时。
a.使用Michelangiolo相似度构建共现矩阵
如前所述,使用共现矩阵作为提取这些关系的手段。我的目标是找到每对标签 之间的关系,通过在所有样本集合 (S) 上使用 IoU (Intersection / Union)在整个样本集合上应用以下计数来实现:
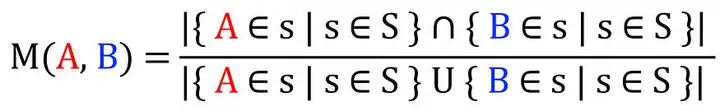
公式来计算一对标签之间的相似性
该算法与Jaccard相似度非常相似。虽然它作用于样本,但这里介绍的作用于元素。
Jaccard相似度和Michelangiolo相似度的区别
对于 40000 个样本,提取相似矩阵大约需要一个小时,结果如下:
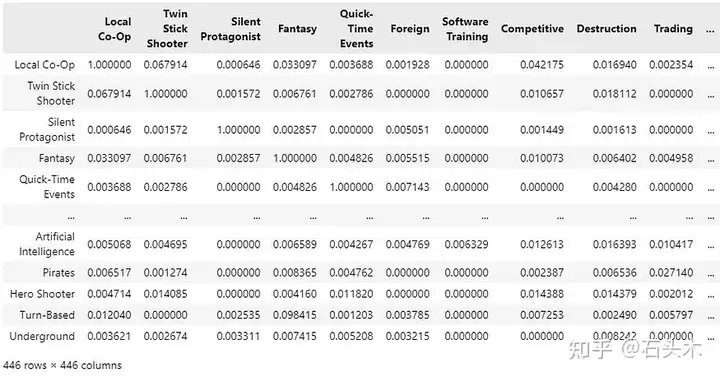
样本列表 S 中所有唯一标签的共现矩阵
让我们对一些非常常见的标签进行top- 10 样本的人工检查,看看结果是否有意义:
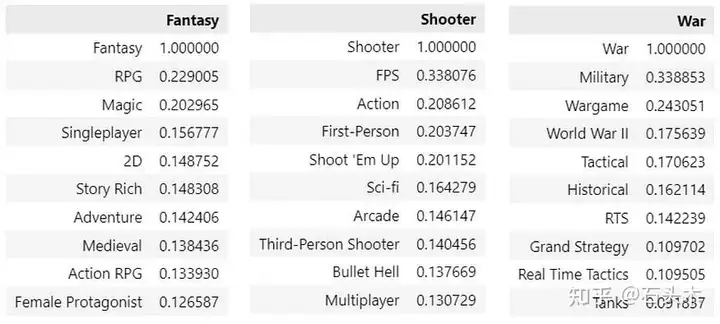
从共现矩阵中提取的样本关系
结果看起来非常有希望!我们从简单的分类数据开始(只能转换为 0 和 1),但我们已经提取了标签之间的语义关系(甚至没有使用神经网络)。
b.使用预训练的神经网络
同样,我们可以使用预训练的编码器提取样本之间的现有关系。然而,这种解决方案忽略了只能从我们的数据中提取的关系,只关注人类语言的现有语义关系。这可能不是一个非常适合在基于零售的数据之上工作的解决方案。
另一方面,通过使用神经网络,我们不需要构建关系矩阵:因此,这是可扩展性的适当解决方案。例如,如果我们必须分析大量 Twitter 数据,我们可以达到 53.300 个标签。从这个数量的标签中计算一个共现矩阵将得到一个大小为 2500,000,000 的稀疏矩阵(相当不实用的壮举)。相反,通过使用输出向量长度为 384 的标准编码器,得到的矩阵的总大小将为 19,200,200。
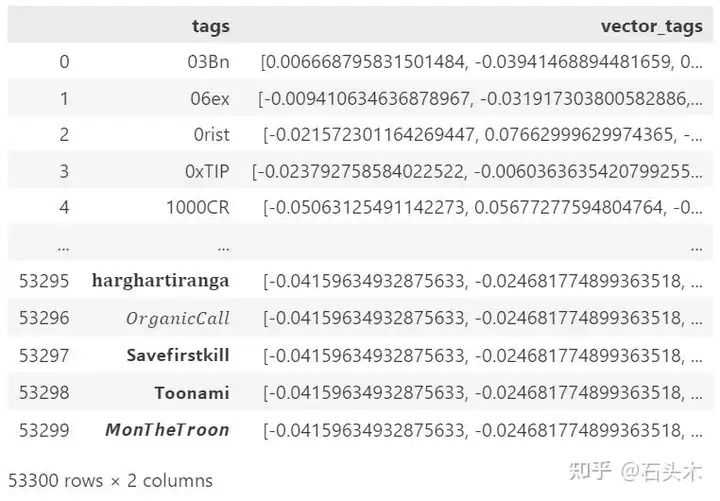
使用预训练编码器的一组编码标签的快照
2.编码查询和样本
我们的目标是构建一个能够支持语义标签搜索的搜索引擎:以我们一直在构建的格式,唯一能够支持这样一个企业的技术是向量搜索。因此,我们需要找到一种合适的编码算法,将我们的样本和查询都转换成向量。
在大多数编码算法中,我们使用相同的算法对查询和样本进行编码。然而,每个样本包含多个标签,每个标签都由一组不同的关系表示,我们需要在单个向量中捕获这些关系。
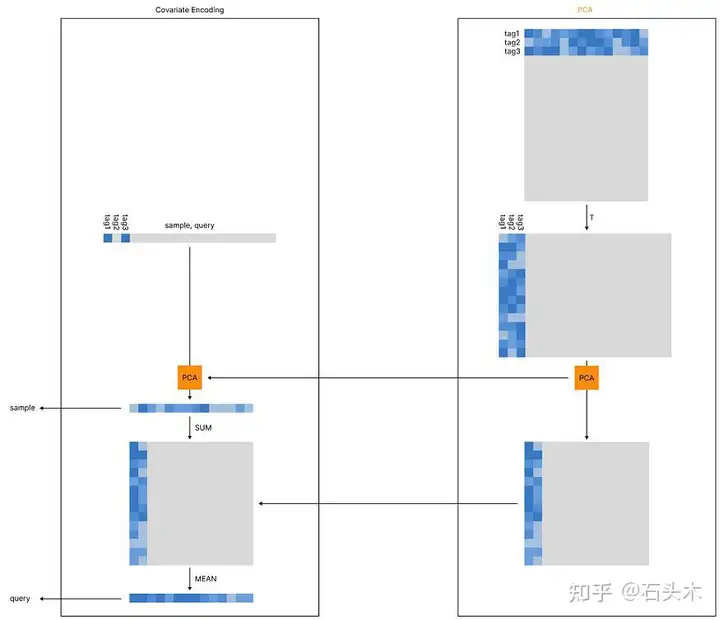
协变量编码
此外,我们需要解决前面提到的可伸缩性问题,我们将通过使用 PCA 模块来解决这个问题(当我们使用共现矩阵时,我们可以跳过 PCA,因为不需要压缩我们的向量)。
当标签的数量变得太大时,我们需要放弃计算共现矩阵的可能性,因为它以平方率扩展。因此,我们可以使用预训练的神经网络(PCA 模块的第一步)提取每个现有标签的向量。例如,all-MiniLM-L6-v2 将每个标签转换成长度为 384 的向量。
然后我们可以对得到的矩阵进行转置,并对其进行压缩:我们将对可用的标签索引使用 1 和 0 来初始编码我们的查询/样本,从而得到与我们的初始矩阵(53,300)长度相同的初始向量。此时,我们可以使用预先计算的 PCA 实例将相同的稀疏向量压缩为 384 个像素。
编码样本
在我们的示例中,该过程刚好在 PCA 压缩之后结束(当激活时)。
编码查询:协变量编码
然而,我们的查询需要进行不同的编码:我们需要考虑与每个现有标签相关联的关系。这个过程是通过首先将我们的压缩向量求和到压缩矩阵(所有现有关系的总和)来执行的。现在我们已经得到了一个矩阵(384x384),我们需要对它求平均值,得到我们的查询向量。
因为我们将使用欧几里得搜索,它将首先优先搜索得分最高的特征(理想情况下,是我们使用数字 1 激活的特征),但它也会考虑额外的次要得分。
加权搜索
因为我们是将向量平均在一起,我们甚至可以在这个计算中应用一个权重,向量受到的影响将不同于查询标签。
3.使用向量检索执行语义标签搜索
你可能会问的问题是:为什么我们要经历这种复杂的编码过程,而不是简单地将这对标签输入到一个函数中,然后获得一个分数 ——f(query, sample)?
如果你熟悉基于向量的搜索引擎,你应该已经知道答案了。通过成对执行计算,在只有 40,000 个样本的情况下,所需的计算能力是巨大的(单个查询可能需要长达 10 秒):这不是一个可扩展的实践。然而,如果我们选择执
行 40,000 个样本的向量检索,搜索将在 0.1 秒内完成:这是一个高度可扩展的实践,在我们的情况下是完美的。
4.验证
一个算法要想有效,就需要被验证。目前,我们缺乏适当的数学验证(乍一看,从 M 中平均相似度得分已经显示出非常有希望的结果,但需要进一步的研究来获得有证据支持的客观指标)。
然而,当使用比较示例进行可视化时,现有的结果是相当直观的。以下是两种搜索方法的最热门搜索结果(你所看到的是分配给这个游戏的标签)。
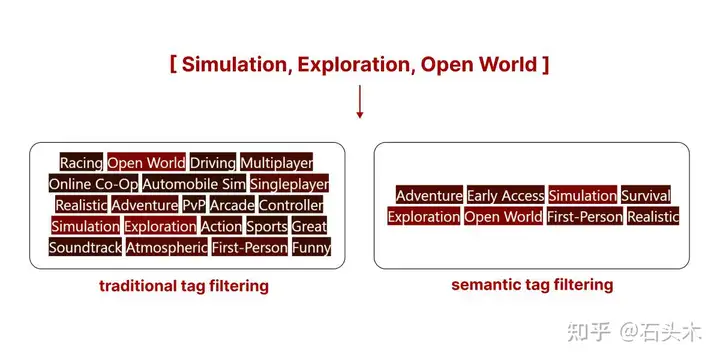
传统标签搜索和语义标签搜索的对比
- 传统标签搜索
我们可以看到,传统搜索可能(没有额外的规则,样本是根据所有标签的可用性进行过滤的,而不是排序的)返回一个标签数量较多的样本,但其中许多标签可能不相关。
- 语义标签搜索
语义标签搜索根据所有标签的相关性对所有样本进行排序,简单来说,它取消了包含不相关标签的样本的资格。
这个新系统的真正优势在于,当传统搜索没有返回足够的样本时,我们可以使用语义标签搜索选择我们想要的尽可能多的样本。
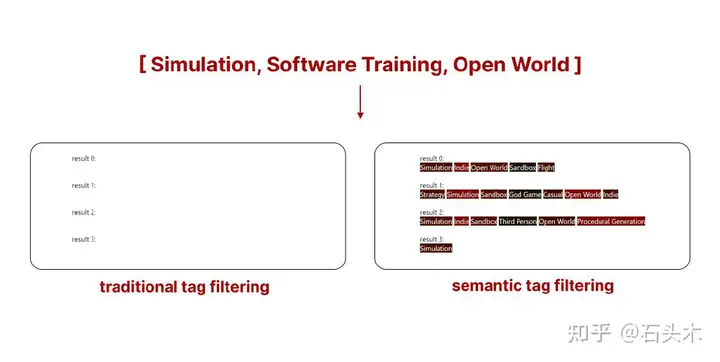
两种搜索的区别在结果的稀缺性面前
在上面的例子中,使用传统的标签过滤不会从 Steam 库中返回任何游戏。然而,通过使用语义标签过滤,我们得到的结果仍然不是完美的,而是与我们的查询匹配的最佳结果。你看到的是匹配我们搜索的前 5 个游戏的标签。
结论
在此之前,如果不采用复杂的方法,如聚类、深度学习或多重 knn 搜索,就不可能同时考虑到它们的语义关系来过滤标签。
该算法提供的灵活性程度应该允许脱离传统的手动标记方法,传统的手动标记方法迫使用户在预定义的标签集之间进行选择,并打开使用 llm 或 vlm
自由地将标签分配给文本或图像的可能性,而不局限于预先存在的结构,为可扩展和改进的搜索方法开辟了新的选择。





