SM 集训记录(2024.11.15 ~ 2024.11.29)
DAY0(2024.11.15)
终于来了www
T2 GYM104787M
首先定义一个副本连通块是只经过编号 \(> n\) 的节点形成的连通块。不难发现一个副本连通块(绿色)会连接着一些编号 \(< n\) 的叶子,然后与原图联通,并且与原图相同部分组成一个对称的连通块。就像下面的图一样:
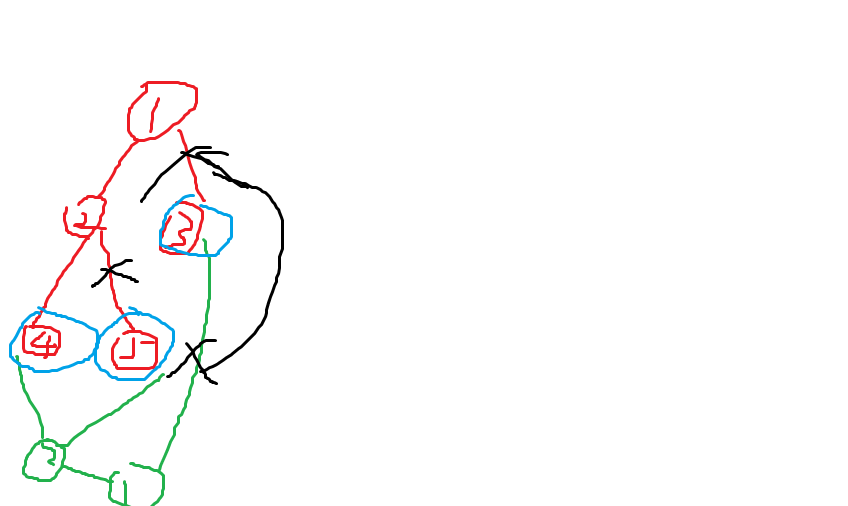
然后假如有 \(lf\) 个叶子(蓝色节点),其实就是要割掉 \(lf - 1\) 条边,且删掉后的图连通。于是把那些删除的边全部翻到原树上,不难发现一个方案合法当且仅当在原树上每个连通块中都有一个叶子。于是直接 \(\mathrm {DP}\) 即可。
关于合法方案的判定
在该题中,一个方案不合法当且仅当两个叶子构成了一个环或者一个点与两个树都不联通。所以这就对应着原树中有两个叶子在一个连通块。反之,该方案合法。- 这启发我们判断充要条件时可以从反面思考。
细节
这里的 $DP$ 设计:设 \(f_u/g_u\) 是节点 \(u\) 所在连通块有一个/没有叶子的方案数,且其子树中的连通块都是合法的。
初始状态:叶子中:\(f_u = 1, g_u = 0\)。
当 \(u\) 遇到一个新的儿子:
qwq
#include<bits/stdc++.h>
#define ll long long
#define pb emplace_back
using namespace std;
const int N = 5000 + 10;
const ll mod = 998244353;
struct edge{
int v, next;
}edges[N << 1];
int head[N], idx;
int n;
bool chosen[N], vis[N];
ll f[N], g[N], pw2[N];
void add_edge(int u, int v){
edges[++idx] = {v, head[u]};
head[u] = idx;
}
int lfcnt;
void dfs(int u, int fa){
//cout << u << " " << fa << "\n";
if(!chosen[u]){lfcnt++; f[u] = 1; g[u] = 0; return;}
f[u] = 0; g[u] = 1; vis[u] = 1;
for(int i = head[u]; i; i = edges[i].next){
int v = edges[i].v; if(v == fa) continue;
dfs(v, u);
f[u] = (f[u] * (g[v] + f[v]) % mod + f[v] * g[u] % mod) % mod;
g[u] = (g[u] * (g[v] + f[v])) % mod;
//cout << u << " " << v << " " << f[u] << " " << g[u] << "\n";
}
}
signed main(){
freopen("tree.in", "r", stdin);
freopen("tree.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n; pw2[0] = 1;
for(int i = 1; i <= n; i++) pw2[i] = 2ll * pw2[i - 1] % mod;
for(int i = 1; i < n; i++){
int x, y; cin >> x >> y;
add_edge(x, y); add_edge(y, x);
}
for(int i = 1; i < n; i++){
int x; cin >> x; chosen[x] = 1;
for(int u = 1; u <= n; u++) vis[u] = 0, f[u] = g[u] = 0;
ll ans = 1;
for(int u = 1; u <= n; u++) if(!vis[u] && chosen[u]) lfcnt = 0, dfs(u, 0), ans = (ans * f[u] % mod * pw2[lfcnt - 1] % mod) % mod;
cout << ans % mod << "\n";
}
return 0;
}
T3 Mod
- Statement
给定长度为 \(n\) 的正整数序列 \(a\),梦梦给出了以下函数:
void mod(int x){
for(int i=1;i<=n;i++)a[i]=a[i]%x;
}
你可以执行这个函数任意次,且每次调用函数的参数可以任意指定,但要求调用的参数 \(x\) 为正整数,请问最终可以得到多少种不同的 \(a\) 序列,答案对 \(998244353\) 取模。
对于 \(50 \%\) 的数据,满足 \(a_i = i\)。
- Solution
首先考虑特殊性质的做法,手玩可以发现,操作过的序列一定形如 \(1, 2, 3, ...., x_1, 0, 1, 2, ...., x_2, 0, 1, 2 ...., x_3, ..... x_n\),且所有数小于 \(x_1 + 1\)。
于是不难发现这也是充要条件,因为我们可以把所有 \(0\) 的位置都插入到取模集合中(注意不一定从小到大)。于是显然可以枚举 \(x_1\),里面套一个 \(O(n ^ 2)\) 的 \(\mathrm {DP}\)。然后对于一般的数据,直接拓展即可。
关于 DP 以及为什么不会算重
首先给出 \(\rm DP\) 设计:设 \(f_{i, j}\) 是原来值为 \(i\),操作后值为 \(j\) 的不同 \(a\) 的数量。
枚举第一个 \(0\) 的位置 \(x\) 进行 \(\mathrm {DP}\),初始状态为 \(f_{x, 0} = 1\)。
转移如下:
- \(f_{i + 1, j + 1} \gets^{+} f_{i, j}\)
- \(if exist a_w = i:\) \(f_{i, j} = \sum_{k = 0}^{x - 1}{f_{lst, k}}(\forall 0 \le j \le {\min(x - 1, i - lst - 1)})\)
qwq
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 500 + 10, mod = 998244353;
int n, a[N], V, vis[N];
ll f[N][N];
void ADD(ll &x, ll y){x = (x + y) % mod;}
ll solve(int s){
memset(f, 0, sizeof f); f[s][0] = 1;
int lst = 0;
for(int i = 1; i <= V; i++){
if(vis[i]){
ll sum = 0;
for(int j = 0; j < s; j++) ADD(sum, f[lst][j]);
for(int j = 0; j <= i - lst - 1; j++) ADD(f[i][j], sum);
lst = i;
}
for(int j = 0; j < s; j++) ADD(f[i + 1][j + 1], f[i][j]);
}
ll ret = 0;
for(int i = 0; i < s; i++) ADD(ret, f[V][i]);
return ret;
}
signed main(){
freopen("mod.in", "r", stdin);
freopen("mod.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n; ll ans = 0;
for(int i = 1; i <= n; i++) cin >> a[i], V = max(V, a[i]), vis[a[i]] = 1;
for(int i = 1; i <= V + 1; i++) ADD(ans, solve(i));
cout << (ans + 1) % mod;
return 0;
}
DAY1
早上打了一场信心赛,AK 了。
下午补了 \(\rm day0 T3\)。
DAY2
晚上尝试和 \(\rm \color{black}l\color{red}arsr\)打一下 \(\rm UNR\),想了一个小时第一题只会
\(\rm T1\) 的 \(O(n^3)\) 做法,还假了(虽然改一下就可以过了)。查询其他人的做题情况,发现都不会 \(\rm T1\),遂放弃。后来写了一下博客,调了一下环境就回宿舍了。
DAY3
早上先补了两个题,然后写了一个 \(\rm \color{black}y\color{red}yc\) 数据结构的题目,对线段树分治有了更多的想法。接着学了一下整体二分,写了一个下午发现数组开小了/ll
感觉效率好低。
傍晚写了一下博客。晚上又打模拟赛,T1 签到,T2 子集容斥,T3 线性基板子题但我不会qwq,T4 神秘,最后 \(100 + 80 + 80 + 20 = 280\)。
DAY4
早上学了线性基。this
下午做里面的练习题。晚上模拟赛,\(\mathrm {T1}\) 花了 \(2h\) 写了一个贪心过掉了所有大样例。然后发现怎么大家都没写完 \(\mathrm {T1}\)?看 \(\mathrm {T2}\) 一点不会啊,怎么还可以更改目标的?\(\mathrm {T3}\) 想了 \(30min\) 会了,直接冲,还剩 \(40min\) 的时候过掉了所有大样例,造了两组 \(\mathrm {hack}\),怎么挂掉了???修修修,发现做法假了。突然意识到应该加个容斥就可以了,我写写写,写一百行,怎么写不完了,呜呜呜。出分,怎么没分?哦等一下就有了,挂分了。这都有 \(rk7\)?哦大家都在看国足。
T2 string
- Statement:
给定 \(n\) 个长度为 \(m\) 的不同的 \(01\) 字符串,一个长度为 \(nm\) 的 \(01\) 字符串 \(S\) 是好的,当且仅当 \(S[1:m],S[m+1:2m],..., S[(n-1)m+1:nm]\) 这 \(n\) 个子串两两不同,且每个子串均为
\(S_1, S_2 ..., S_n\) 中的一个。现在你有一个打字机,有 \(p\) 的概率打错字(即 \(1\) 打成 \(0\),\(0\) 打成 \(1\))。你足够聪明,希望可以打出好的字符串,且可以根据当前打出的字符动态调整策略,问打出好的字符串的概率。\(n, m \le 10^3\)。
- Solution:
不妨把所有操作都放到 \(\mathrm {Trie}\) 树上进行。不难发现一个合法的字符串其实就是在树上走 \(n\) 次,每次走出一个字符串集合内的字符串,换而言之,就是每条 \(\mathrm {Trie}\) 上的边在字符集中出现的次数恰好等于经过的次数。因为在遍历的过程中可以改变目标,所以直接考虑字符串是不可行的,只能一位位的进行考虑。
假设现在走到节点 \(u\),它的左子树对应的那条边需要经过 \(c_1\) 次,右子树的是 \(c_2\)。那么可以转化为有 \(c_1\) 个 \(0\),\(c_2\) 个 \(1\),通过 \(c_1 + c_2\) 次操作恰好打出。可以直接 \(\mathrm {DP}\)。然后再计算它的两个子节点的答案,乘法原理即可。时间复杂度 \(O(nm)\)。
qwq
#include<bits/stdc++.h>
#define ll long long
#define db double
using namespace std;
const int N = 2e6 + 10, M = 1e3 + 10;
db ans = 1, f[M][M];
struct Trie{
int son[N][2], siz[N], tot = 1;
void ins(string str) {
int p = 1;
for(int i = 0; i < str.size(); i++) {
int id = str[i] - '0'; if(!son[p][id]) son[p][id] = ++tot;
p = son[p][id]; siz[p]++;
}
}
void solve(int u) {
// cout << u << " " << siz[son[u][0]] << " " << siz[son[u][1]] << " " << f[siz[son[u][0]]][siz[son[u][1]]] << " " << ans << "\n";
if(!u) return; ans = ans * f[siz[son[u][0]]][siz[son[u][1]]];
solve(son[u][0]); solve(son[u][1]);
}
}tr;
int n, m;
signed main(){
// system("fc string6.out string.out");
freopen("string.in", "r", stdin);
freopen("string.out", "w", stdout);
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
db tb; cin >> n >> m >> tb; tb = max(tb, 1 - tb);
const db p = tb, ip = 1 - tb;
for(int i = 1; i <= n; i++) {
string str; cin >> str; tr.ins(str);
} f[0][0] = 1;
for(int i = 0; i <= n; i++) {
for(int j = 0; j <= n; j++) {
if(i == 0 && j == 0) continue;
if(i > j) f[i][j] = f[i - 1][j] * p + (j == 0 ? 0.0 : (f[i][j - 1] * ip));
else f[i][j] = (j == 0 ? 0.0 : (f[i][j - 1] * p)) + (i == 0 ? 0.0 : (f[i - 1][j] * ip));
// cout << i << " " << j << " " << f[i][j] << "\n";
}
} tr.solve(1);
cout << fixed << setprecision(12) << ans;
return 0;
}
DAY5
写了一些线性基,补了两道 \(\rm DP\),晚上水分大赛。
DAY6
直接变成暴力老哥,\(100 + 0 + 72 + 40 = 212\)。但是 \(T3\) 赛后一句话我就会了,\(T2\) 也是,是瓶颈期了嘛?QAQ
DAY7
T3 match
- Statement:
\(\rm Floating Island\) 正在举办一年一度的魔法比赛,共计有 \(n\) 个人参加,有三种不同的场地,每一名选手在不同的场地上有不同的排名。作为比赛的裁判,小 \(1\) 每次可以任意选择两名没有被淘汰的选手进行比赛,并且指定一种比赛场地,然后在这种场地上较弱的选手会被淘汰。
由于魔法的世界在不断地变化,现在有若干的询问和修改的事件,每一次修改会交换两名选手在某一种场地上的排名。
每次询问,小 \(1\) 想知道 \(x\) 号选手有没有可能赢得比赛。请你帮助她回答这些问题。
\(n, q \le 10^5\)
- Solution:
首先对于每个序列 \(a_i\) 向 \(a_{i + 1}\) 连一条有向边,不难发现只有在三个链的链头组成的强联通分量中的点才可以打败所有点。然后观察发现这个强联通分量 \(S\) 满足是三个链每个长度为 \(len\) 的前缀组成的点集,且点集大小为 \(len\)。换句话说,就是要找到一个最小的 \(len\),使得 \(S_0 = \{a_{0, 1}, a_{0, 2}...., a_{0, len}\}, S_1 = \{a_{1, 1}, a_{1, 2}, ...., a_{1, len}\}, S_2 = \{a_{2, 1} ...., a_{2, len}\}\) 都相同。
那么维护第 \(i\) 个人在三个排列最小的位置 \(L_i\),最大的位置 \(R_i\)。对区间 \([L_i, R_i - 1]\) 区间 \(+1\),最后的答案就是第一个 \(0\) 的位置。线段树直接维护即可。时间复杂度 \(O((n + q) \log n)\)。
考场上暴力 \(\rm tarjan\) 拿了 \(72pts\)。这启发我们对于图论问题不一定需要观察整个图的形态,而只需要关注答案相关,然后转化即可。
qwq
#pragma GCC optimize(3, "Ofast", "inline")
#include<bits/stdc++.h>
#define int long long
using namespace std;
int min(int x, int y){return (x < y) ? x : y;}
int max(int x, int y){return (x > y) ? x : y;}
void chkmin(int& x, int y){if(x > y) x = y;}
void chkmax(int& x, int y){if(x < y) x = y;}
const int N = 1e5 + 10;
int n, a[3][N], rk[3][N], Lmn[N], Rmx[N], ans;
namespace Segtree{
#define ls (o << 1)
#define rs (o << 1 | 1)
#define mid (l + r >> 1)
int tag[N << 2], tmin[N << 2];
void pushup(int o){tmin[o] = min(tmin[ls], tmin[rs]);}
void addtag(int o, int v){tmin[o] += v; tag[o] += v;}
void pushdown(int o){
if(!tag[o]) return;
addtag(ls, tag[o]); addtag(rs, tag[o]); tag[o] = 0;
}
void Segadd(int o, int l, int r, int s, int t, int v){
if(s > t) return;
if(s <= l && r <= t){addtag(o, v); return;}
pushdown(o);
if(s <= mid) Segadd(ls, l, mid, s, t, v);
if(mid < t) Segadd(rs, mid + 1, r, s, t, v);
pushup(o);
}
int fid(int o, int l, int r){
if(l == r) return l;
pushdown(o); //cout << o << " " << l << " " << mid << " " << r << " " << tmin[ls] << "\n";
if(tmin[ls] == 0) return fid(ls, l, mid);
return fid(rs, mid + 1, r);
}
} using namespace Segtree;
void upd(int x, int rkqwq, int id){
// cout << x << " " << rkqwq << " " << id << "\n";
Segadd(1, 1, n, Lmn[x], Rmx[x] - 1, -1);
rk[id][x] = rkqwq; Lmn[x] = Rmx[x] = rk[0][x];
for(int i = 1; i < 3; i++) chkmin(Lmn[x], rk[i][x]), chkmax(Rmx[x], rk[i][x]);
Segadd(1, 1, n, Lmn[x], Rmx[x] - 1, 1);
}
signed main(){
freopen("match.in", "r", stdin);
freopen("match.out", "w", stdout);
// system("fc match.out match6.ans");
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T; cin >> n >> T;
for(int id = 0; id < 3; id++){
for(int j = 1; j <= n; j++){
cin >> a[id][j]; rk[id][a[id][j]] = j;
}
}
for(int i = 1; i <= n; i++){
Lmn[i] = Rmx[i] = rk[0][i];
for(int id = 1; id < 3; id++) chkmin(Lmn[i], rk[id][i]), chkmax(Rmx[i], rk[id][i]);
Segadd(1, 1, n, Lmn[i], Rmx[i] - 1, 1);
}
ans = fid(1, 1, n);
while(T--){
int opt; cin >> opt;
if(opt == 2){
int id, x, y; cin >> id >> x >> y; id--;
int rkx = rk[id][x], rky = rk[id][y];
upd(x, rky, id); upd(y, rkx, id);
ans = fid(1, 1, n); //cout << ans << "\n";
}
else{
int x; cin >> x; cout << (rk[0][x] <= ans ? "Yes" : "No") << "\n";
//cout << "Yes" << "\n";
}
}
return 0;
}
T2 wolf
- Statement:
\(\rm Floating Island\) 中存在一个狼群。狼群中的 \(n\) 只狼被编号为 \(1-n\)。
对于第 \(i\) 只狼,它在初始时位于网格的顶点 \((x_i,y_i)\) 处。在每一轮移动中,它都会选择移动到相邻的 \(4\) 个网格顶点之一,即 \((x - 1, y)\)、\((x + 1, y)\)、\((x, y - 1)\) 和 \((x,y + 1)\) 之一。
在 \(m\) 轮移动结束后,狼群中的 \(n\) 只狼都移动到了同一个网格顶点。求满足条件的狼的移动路径方案数,对 \(10^9 + 7\) 取模。
两种移动路径方案被认为不同,当且仅当存在某一轮移动中,某一只狼的移动方向不同。
\(n \le 50, x_i, y_i \le 10^5\)
- Solution:
不妨考虑一个点可以走到那些点,显然是一个斜的正方形,于是不妨将棋盘旋转 \(45\) 度,一个点的坐标就变成了 \((x + y, x - y)\)。此时一次移动等价于 \((\pm 1, \pm 1)\) 的移动,于是两个坐标就可以分开考虑。枚举最后走到的 \(x + y\) 或者 \(x - y\) 然后推柿子就可以了。
看到 \(x, y\) 较大的情况,可以通过一些方法将两维分开考虑。
DAY8
忘了。
11.26
T4
首先不难发现加入一个字符后,整个 \(S\) 的 \(\rm border\) 都可以对答案产生贡献,具体的,对于长度为 \(k\) 的 \(\rm border\),可以对 \(k\) 的查询产生 \(1\) 的贡献。于是显然可以 \(O(n ^ 2)\)。(你说的对但是考场上写了暴力跳可以过()不难发现,这等价于建出串的失配树,然后每次对新的点所在失配树父亲到根链加。离线可以树剖,但是在线显然不行。
那么不妨考虑使用树剖的思想,通过设置重儿子快速维护链上信息。然后考虑到这是 \(\rm border\) 上的操作,联想到这样一个性质:
- 一个串所有的 \(\rm border\) 可以被分为 \(\log n\) 个等差数列。
于是我们对于一个点 \(u\),设它在失配树上的父亲是 \(fa\),那么加入 \(u\) 有儿子 \(2u - fa\),将它设成重儿子即可。然后套一个树状数组,不难发现这样的时间复杂度是 \(O(n \log^2 n)\) 的。但是题解说是 \(O(n \log n)\) 而且我不会证/fad
note
- Trie 整体异或可以直接打标记,整体 \(+1\) 就从低位到高位贪心就行了。

