2024.8.14 DP Round 2
A.store
Statement:
有 \(n(1 \le n \le 100)\) 个果盘，其中第 \(i\) 个果盘有 \(a_i\) 个水果，容量是 \(b_i(a_i \le b_i \le 100)\)。一次操作可以将一个水果从一个果盘放到另一个果盘中，现在要将所有水果放到最少的盘子中，问最少要用多少盘子以及最少需要多少操作。
Solution:
第一问容易贪心算出。注意到值域很小，于是直接设 \(f_{i, j, k}\) 是考虑前 \(i\) 个果盘，选了 \(j\) 个果盘作为最后有水果的果盘时，以及还剩 \(k\) 个可以放置的水果，然后就做完了。
B.huffman
Statement:
按字典序顺序给出 \(n(1 \le n \le 500)\) 个字符串，第 \(i\) 个字符串出现的次数是 \(a_i\)，现在你要将他们每个分别映射到一个 \(k(1 \le k \le 60)\) 进制的字符串，满足：
-
没有任意一个映射后的字符串是另一个映射后的字符串的前缀。
-
映射后的字符串的字典序顺序必须与原来的字符串顺序一致。
-
\(\sum_{i = 1}^n {len_i a_i}\) 最小，其中 \(len_i\) 是字符串映射后的长度。
Solution:
注意到由于字典序顺序不变，于是一个区间 \([l, r]\) 最后的形态一定是 \([1, 1, 2, 2, ...,k - 1, k, k]\)。即会被分为至多 \(k\) 个单调不降的连续区间。于是考虑区间 \(\rm DP\)，设 \(f_{l, r, cnt}\) 是将区间 \([l, r]\) 分为至多 \(cnt\) 个区间最小的 \(\sum len_ia_i\)，其中 \(f_{l, r, 1}\) 是 \([l, r]\) 区间分为“一个”区间最小的代价，这个东西的定义非常令人不解，但是我们可以在 \(cnt > 1\) 的状态转移方程中得到。
考虑如何转移：
-
\(cnt > 1\): \(f_{l, r, cnt} = \min_{k = l}^{r - 1} f_{l, k, 1} + f_{k + 1, r, cnt - 1}\)
-
\(cnt = 1\): \(f_{l, r, 1} = f_{l, r, cnt} + \sum_{i = l}^r a_i\)
于是得到了一个 \(O(n^3k)\) 的做法（其实拿到树上更好理解，但是我在想的时候还是用的区间）。
先讲正解，注意到分割的方式是 \(1, k - 1\)，其实我们可以利用倍增的思想分为 \(k / 2, k - k / 2\) 的区间，预处理出需要计算的区间，于是可以在 \(O(n^3 \log k)\) 的时间做了。
接下来讲如何卡常：
-
手写 \(\min/\max\)：\(\rm STL\) 中的 \(\min/\max\) 是很慢的，大概可以快个 \(0.5s - 1.5s\) 左右
-
手动 \(\rm O3\)：
#pragma GCC optimize(3, "Ofast", "inline")，真的很快！！！ -
减少 \(\rm \text {cache miss}\)：通过改变循环枚举顺序，使下标尽量连续，将 \(\rm cache\) 用到极致。
C.diversity
Statement:
给定一个 \(n \times m(1 \le n, m \le 200)\) 的矩阵，只由 # 和 . 组成。对于一个子矩阵，它的多样性定义为：
-
假如这个矩阵的字符都一样，则该矩阵的多样性为 \(0\)。
-
假设将这个矩阵从一条横线隔开成为两个子矩阵，设两个矩阵的多样性为 \(a, b\)，则该矩阵的多样性为 \(\max(a, b) + 1\)。
-
假设将这个矩阵从一条竖线隔开成为两个子矩阵，设两个矩阵的多样性为 \(a, b\)，则该矩阵的多样性为 \(\max(a, b) + 1\)。
问整个矩阵的多样性为多少。
Solution:
非常好的一道题。
首先容易有一个 \(O(n^5)\) 的暴力 \(\rm DP\)：设 \(f_{u, d, l, r}\) 是 \([u, d], [l, r]\) 这个矩阵的多样性，\(O(n)\) 枚举即可。
然后注意到答案不会很大（这里的答案上界是 \(\lceil \log n\rceil + \lceil \log m \rceil\)，因为可以一直从中间横着割开，然后割成一条后再竖着割变为一个格子），于是可以考虑换量。设 \(f_{u, d, l, ans}\) 是满足 \([u, d][l, f_{u, d, l, ans}]\) 的多样性 \(\le ans\) 最大的 \(f_{u, d, l, ans}\)。转移：
-
横着割：\(f_{u, d, l, ans} = \max_{k = u}^{d - 1}{\min(f_{u, k, l, ans - 1}, f_{k + 1, d, l, ans - 1})}\)
-
竖着割：\(f_{u, d, l, ans} = f_{u, d, l, f_{u, d, l, ans - 1} + 1, ans - 1}\)
这样就有了一个 \(O(n^4 \log n)\) 的算法。注意到上面的转移瓶颈在于横着割的枚举。
然后注意到这是一个区间 \(\rm DP\) 的形式，于是可以猜出满足决策单调性（证明可以用蒙日矩阵），于是可以均摊 \(O(1)\) 做了，于是有了 \(O(n^3 \log n)\) 的做法。
D.zombie
Statement:
（原题面）
舞王僵尸的最新唱片 “抓住脑子啃啊啃” 在僵尸界的人气正急速飙升。他们准备在戴夫家门前的花园前表演。他们所在的位置排成了一条直线，每个舞王僵尸的位置可以用一个正整数坐标表示。
然而，戴夫在该直线上 \(m\) 个位置隐藏有无限土豆雷。他们暂时与舞王僵尸不在同一个位置上。也就是说，这 \(n + m\) 个坐标都互不相同。我们从左往右将舞王僵尸从 \(1\) 到 \(n\) 标号，将土豆雷从 \(1\) 到 \(m\) 标号。
现在你给舞王僵尸编订了一个舞步顺序。每次舞步可以让所有舞王僵尸向左或向右行进一步，此时它们的坐标会 \(−1\) 或 \(+1\)。每当一个舞王僵尸移动到与土豆雷一样的位置时，土豆雷就会爆炸，从而使舞王僵尸死亡并消失。这个无限土豆雷自始至终不会随着爆炸消失或移动位置，可以消灭任意多的舞王僵尸。
最后，所有的舞王僵尸在你的舞步顺序下都陆续死亡。整个死亡过程可以简化为 \(n\) 个整数
\(p_1, p_2, ..., p_n\) 的死亡序列，其中 \(p_i\) 代表 \(i\) 号舞王僵尸被 \(p_i\) 号土豆雷炸死。容易发现，若你编订的舞步顺序不同，死亡序列也就有可能产生变化。
而两种死亡序列 \(p_1, p_2, ..., p_n\) 和 \(q_1, q_2, ..., q_n\) 本质不同，当且仅当 \(\exists i \in [1, n], p_i \ne q_i\)。
给出每个舞王僵尸和土豆雷的坐标，求有多少种本质不同的死亡序列，答案对 \(10^9 + 7\) 取模。
\(n, m \le 10^5, a_i \le 10^9\)
Solution:
首先注意到一个 \(\rm zombie\) 只可能被夹着它的两个土豆雷炸死，先考虑一个 \(zombie_j\) 可以选择向左边死亡的条件，显然是 \(\forall j \in S_{right}, rd_j < rd_i\)。向右边的条件也是一样。注意到一个元素有两个信息，而且这是一个偏序问题，于是可以放到坐标系上讨论。具体的，对于一个 \(zombie_i\)，我们用 \((ld_i, rd_i)\) 来描述它。考虑一个点选左边带来的影响：
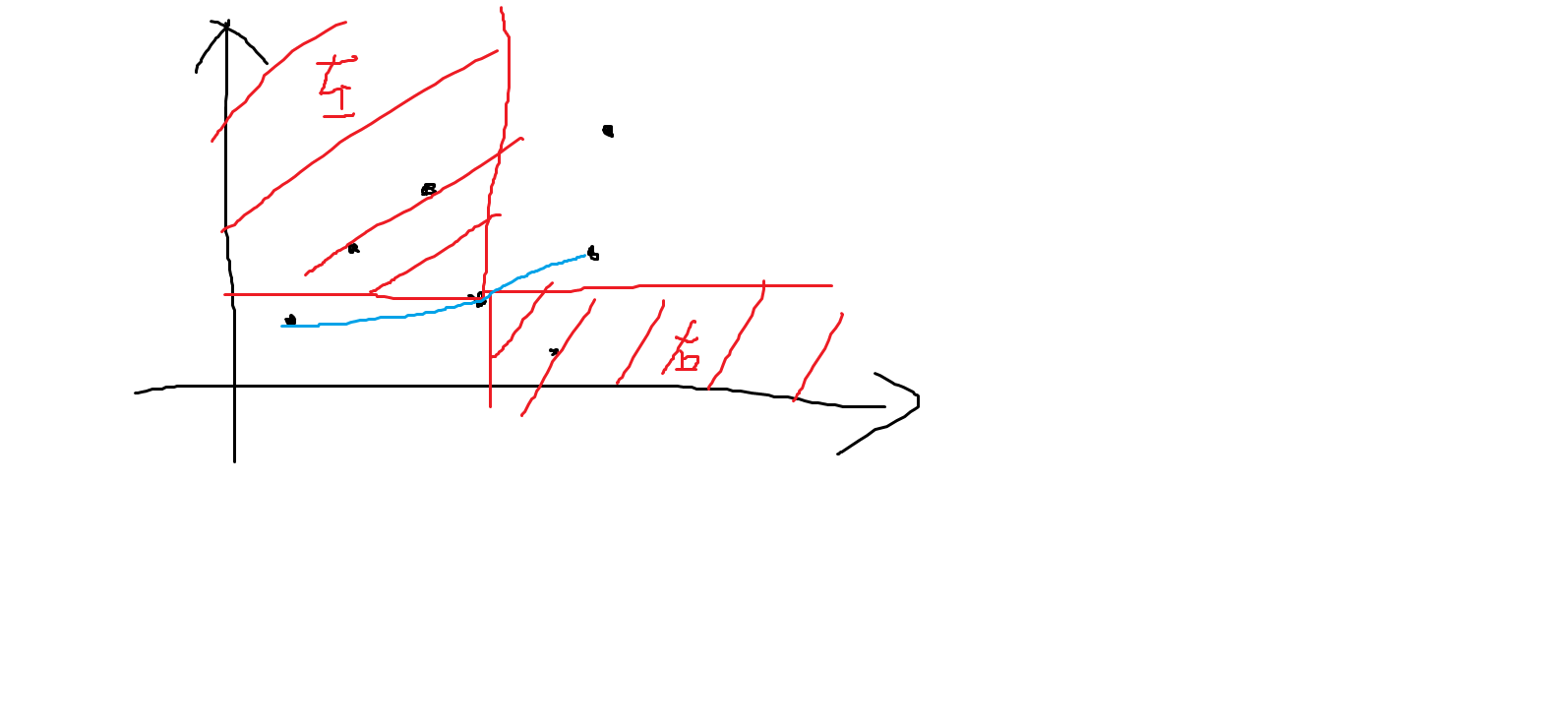
显然假如选左边，它的左上方的所有点都只能选左边，右边同理。于是我们可以发现，上升子序列和合法的选择方案构成一个双射。首先考虑上升子序列向选择方案的映射，我们将在上升子序列的点选左边，覆盖到的点显然也要同时选，而剩下的点选右边即可。然后检查反射，注意到对于不同的上升子序列，其中不同的点覆盖的点显然会至少有一个会在一个序列不被覆盖到而另一个不会被覆盖到，这个画图不难知道。于是那个树状数组直接做即可，时间复杂度 \(O(n \log n)\)。
