GJOI 2024.7.15 总结
T1 CF1607E
简单题，直接模拟即可。
T2 CF1614C
Solution:
容易发现一种可行的构造方案就是对于每个 \(a_i\) 以及包含它的操作 \(C_{i_1, i_2 ... i_t}\)，令 \(a_i = V_{i_1} \& V_{i_2} \& ...V_{i_t}\) 即可。直接硬上线段树即可。
考虑到位运算位之间互不影响的性质，接着我们从分别考虑每一位对答案的贡献。统计的时候分类讨论一下就可以了。
qwq
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int n, m, a[N], two[50];
namespace Segtree{
#define ls (o << 1)
#define rs (o << 1 | 1)
#define mid (l + r >> 1)
int tag[N << 2];
void build(int o, int l, int r){
tag[o] = (1ll << 31) - 1;
if(l == r) return;
build(ls, l, mid); build(rs, mid + 1, r);
}
void pushdown(int o){
if(tag[o] != (1ll << 31) - 1){
tag[ls] &= tag[o]; tag[rs] &= tag[o];
tag[o] = (1ll << 31) - 1;
}
}
void addtag(int o, int l, int r, int s, int t, int val){
if(s <= l && r <= t){tag[o] &= val; return;}
pushdown(o);
if(s <= mid) addtag(ls, l, mid, s, t, val);
if(mid < t) addtag(rs, mid + 1, r, s, t, val);
}
void getval(int o, int l, int r){
if(l == r){a[l] = tag[o]; return;}
pushdown(o); getval(ls, l, mid); getval(rs, mid + 1, r);
}
}
using namespace Segtree;
int calc(int bitid){
int cnt[2] = {1, 0};
for(int i = 1; i <= n; i++){
bool f = (a[i] & (1 << bitid));
int c[2]; c[0] = (cnt[0] + cnt[f]) % mod; c[1] = (cnt[1] + cnt[f ^ 1]) % mod;
cnt[0] = c[0]; cnt[1] = c[1];
}
return cnt[1];
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T; cin >> T; two[0] = 1;
for(int i = 1; i <= 40; i++) two[i] = (two[i - 1] * 2) % mod;
while(T--){
cin >> n >> m; build(1, 1, n);
for(int i = 1; i <= m; i++){
int l, r, v; cin >> l >> r >> v;
addtag(1, 1, n, l, r, v);
}
getval(1, 1, n); int ans = 0;
// for(int i = 1; i <= n; i++) cout << a[i] << " ";
// cout << calc(0) << "\n";
for(int bit = 0; bit <= 30; bit++) ans = (ans + calc(bit) * two[bit] % mod) % mod;
cout << ans << "\n";
}
return 0;
}
T3 CF1611G
Solution:
好题。
首先观察性质，容易发现棋盘上有两类点，他们按对角线为分类，两类点互不可达。换句话说，如果我们对棋盘进行黑白交替染色，可以得到黑白两类点，而且他们互不影响，于是可以分开讨论，下面默认只考虑一个颜色的点对。
其次我们进一步的观察，考虑怎么样的两个点可以被一次吃掉，即怎么样的 \((i, j)\) 点对中 \(i\) 可以走到 \(j\)。我们不妨设 \(i\) 在 \(j\) 的上方，即 \(y_i < y_j\)。通过画图可以发现 \(j\) 一定在 \(i\) 所在两条对角线的夹角下方。如下图：
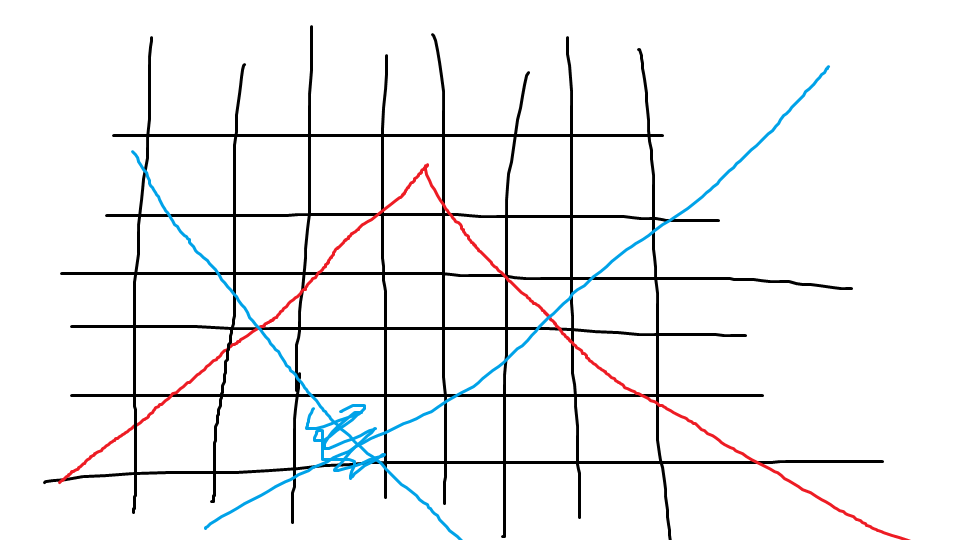
显然红点是可以到蓝点的，但是这样我们并不好去判断。于是我们再次考虑转化问题：，如果拿两条对角线去夹这个蓝点，可以发现蓝点在红点的夹角区域则等价于蓝点两条对角线都在红点两条对角线的下方。点 \((x, y)\) 的两条对角线可以表示为 \(x + y\) 和 \(x - y\)。定义点 \((x, y)\) 的新坐标为 \((x + y, x - y)\)。于是一条合法的路径则满足新坐标的两个数值都单调不下降，问题就变为将原序列任意排列后，最少分为多少个子序列，满足每个子序列的两维坐标均单调不下降。
于是我们一个贪心即可解决问题了。
qwq
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6 + 10, INF = 1e18;
struct point{
int x, y;
}p[N], _p[N];
int n, m, tot, _t;
set<int> s;
bool cmp(struct point p1, struct point p2){return (p1.x != p2.x ? p1.x < p2.x : p1.y < p2.y);}
int calc(){
sort(p + 1, p + tot + 1, cmp); int ans = 0; s.clear();
if(tot){
ans = 1; s.insert(p[1].y);
for(int i = 2; i <= tot; i++){
if(*s.begin() > p[i].y) s.insert(p[i].y), ans++;
else{
auto it = s.upper_bound(p[i].y); it--;
s.erase(*it); s.insert(p[i].y);
}
}
}
return ans;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
int T; cin >> T;
while(T--){
cin >> n >> m; tot = _t = 0;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
char c; cin >> c;
if(c - '0'){
if((i + j) & 1) p[++tot] = {i + j, i - j};
else _p[++_t] = {i + j, i - j};
}
}
}
int ans = calc();
for(int i = 1; i <= _t; i++) p[i] = _p[i]; tot = _t;
cout << ans + calc() << "\n";
}
return 0;
}
T4 序列：
Statement:
给定 \(n, x\) 和一个长度为 \(n\) 的序列 \(a\)。问 \(a\) 中有多少个非空子序列，满足对于任意两个不同元素的异或值均大于等于 \(x\)。\(n \le 10^5\)，\(a_i, x \le 2^{60}\)。
Solution:
套路题。
首先我们找到 \(x\) 的最高位 \(bst\)，并将 \(a\) 中的元素按从 \(60\) 位到 \(bst\) 组成的样式分类。容易发现对于任意在不同两类的数对异或值一定是大于 \(x\) 的，因为他们显然有一位是不同的。于是我们每类单独讨论并计算出方案数，再将每类方案数乘起来即可。
对于一类中的数，我们再按 \(bst\) 上是 \(0\) 还是 \(1\) 分类。观察可知，同一类数中至多选 \(2\) 个数。原因是加入有 \(3\) 个数时，就必然会有两个数 \(bst\) 位是一样的，异或后显然小于 \(x\)。
-
对于选 \(0\) 个数的情况：显然方案数为 \(1\)。
-
对于选 \(1\) 个数的情况：显然方案数为数字个数。
-
对于选 \(2\) 个数的情况：
首先肯定是选一个 \(bst\) 位上是 \(1\) 以及一个为 \(0\) 的。
考虑将为 \(0\) 的从 \(bst - 1\) 位为始建一颗 \(\rm Trie\) 树。对于一个 \(bst\) 位为 \(1\) 的 \(a_i\)，套路的在树上从高位到低位走。假设我们考虑到第 \(bit\) 位，走到节点 \(u\)，有两种情况：
-
\(x\) 该位为 \(1\)，则我们向 \(u\) 节点 \(a_i\) 所对应的反方向的子树递归计算。
-
\(x\) 该位为 \(0\)，\(a_i\) 所对应的反方向的子树中所有数均是合法的，加入答案，并向 \(a_i\) 所对应的方向的子树递归计算。
qwq
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 10, M = 2, mod = 998244353;
namespace Trie{
int ch[N * 60][M], siz[N * 60], cnt = 1;
void init(){
for(int i = 1; i <= cnt; i++){
siz[i] = 0; ch[i][0] = ch[i][1] = 0;
}
cnt = 1;
}
void insert(int x, int bit){
int o = 1; siz[o]++;
for(int i = bit; i >= 0; i--){
bool f = (x & (1ll << i));
if(!ch[o][f]) ch[o][f] = ++cnt;
o = ch[o][f]; siz[o]++;
}
}
int getans(int x, int bit, int upd){
int o = 1, ret = 0;
for(int i = bit; i >= 0; i--){
if(o == 0) break;
bool f = (x & (1ll << i)), pot = (upd & (1ll << i));
if(pot == 0){
ret = (ret + siz[ch[o][f ^ 1ll]]) % mod;
// cout << o << " " << bit << " " << f << "\n";
o = ch[o][f];
}
else o = ch[o][f ^ 1ll];
}
// cout << x << " " << o << " " << siz[o] << "\n";
if(o) ret = (ret + siz[o]) % mod;
return ret;
}
}
using namespace Trie;
int n, upd, a[N], b[N], bst, tot;
struct zsw{
int fir, nxt;
}num[N];
bool cmp(struct zsw z1, struct zsw z2){return z1.fir < z2.fir;}
int calc(){
int ret = tot + 1;
for(int i = 1; i <= tot; i++) if(!(b[i] & (1ll << bst))) insert(b[i], bst);
for(int i = 1; i <= tot; i++) if(b[i] & (1ll << bst)) ret = (ret + getans(b[i], bst, upd)) % mod;
return ret;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> n >> upd; int t = 0, tmp = upd;
for(int i = 1; i <= n; i++) cin >> a[i];
while(tmp){
if(tmp & 1ll) bst = t;
tmp >>= 1; t++;
}
// cout << bst << "\n";
for(int i = 1; i <= n; i++) num[i].fir = (a[i] >> (bst + 1)), num[i].nxt = (num[i].fir << (bst + 1)) ^ a[i];
sort(num + 1, num + n + 1, cmp); b[++tot] = num[1].nxt; int ans = 1; num[n + 1].fir = -1; int d = 0;
for(int i = 2; i <= n + 1; i++){
if(num[i].fir != num[i - 1].fir){
ans = (ans * calc()) % mod; tot = 0;
init(); d++;
}
b[++tot] = num[i].nxt;
}
cout << (ans - 1 + mod) % mod;
return 0;
}
