第二题 题解

一、题目：

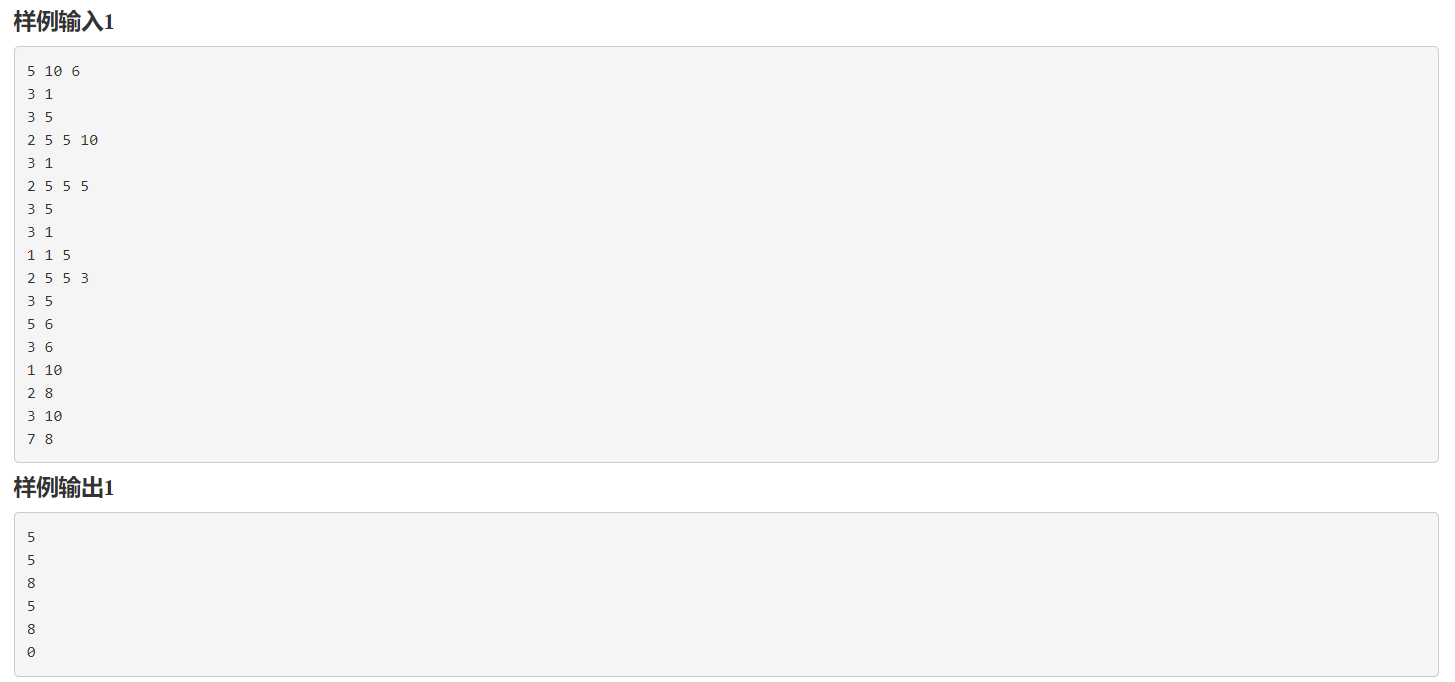
二、思路：

这道题的思路也非常的巧妙。

为了方便叙述，我们将操作 3 称作“小询问”，将需要输出答案的询问称为“大询问”。

将操作按照时刻从大到小排序，依次扫描每个操作，并将大询问 \([l,r]\) 挂在对应的 \(l\) 上。维护以下数据结构。

• 对每个位置维护一个 vector 数组，数组中存储一些小询问的出现时刻。
• 一个 set，维护非空的 vector 数组的下标。
• 一个树状数组，以时刻为下标，存储小询问的答案。

对当前扫描到的操作类型分类讨论，时刻为 \(t\)。

• 当前操作是一个对位置 \(x\) 的一个小询问。

  将时刻 \(t\) 存到位置 \(x\) 的 vector 数组中。实时维护好 set。

• 当前操作是对区间 \([L,R]\) 的覆盖，覆盖的值为 \(v\)。

  将 set 中处于 \([L,R]\) 的那些 vector 中存储的时刻取出来，对于每个时刻，在树状数组中单点修改成 \(v\)。

  然后将这些 vector 清空，并将 set 维护好。

• 当前操作是交换 \((x,y)\)。

  直接将 \(x\) 的 vector 和 \(y\) 的 vector 进行交换。并维护好 set 即可。

对于挂在当前时刻的所有询问。直接在树状数组上查询区间和。

考虑这样做为什么是对的。

我们可以发现，对于一个出现在时刻 \(t\)、对位置 \(x\) 的小询问，只有距离 \(t\) 最近的区间覆盖可以成为这个小询问的答案。所以我们倒序扫描每个操作，在每个区间覆盖之后立即清空所有可以覆盖到的 vector 数组。

树状数组的作用只是快速维护前缀和。

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <set>

using namespace std;
typedef long long LL;
#define FILEIN(s) freopen(s, "r", stdin)
#define FILEOUT(s) freopen(s, "w", stdout)
#define mem(s, v) memset(s, v, sizeof s)

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int MAXN = 1e6 + 5;

int n, m, Q;
LL tr[MAXN], ans[MAXN];

struct Operation {
    int opt, l, r, x;
}ope[MAXN];

vector<pair<int, int> >query[MAXN];
vector<int>vec[MAXN];

set<int>S;
set<int>::iterator it;

#define lowbit(x) (x & (-x))

inline void add(int p, int x) {
    for (; p <= m; p += lowbit(p))
        tr[p] += x;
}

inline LL sum(int p) {
    LL res = 0;
    for (; p; p -= lowbit(p))
        res += tr[p];
    return res;
}

int main() {
    n = read(); m = read(); Q = read();
    for (int i = 1; i <= m; ++ i) {
        ope[i].opt = read();
        if (ope[i].opt == 1) {
            ope[i].l = read(); ope[i].r = read();
        }
        else if (ope[i].opt == 2) {
            ope[i].l = read(); ope[i].r = read(); ope[i].x = read();
        }
        else if (ope[i].opt == 3) {
            ope[i].x = read();
        }
    }
    for (int i = 1; i <= Q; ++ i) {
        int l = read(), r = read();
        query[l].push_back({ r, i });
    }
    for (int i = m; i >= 1; -- i) {
        if (ope[i].opt == 3) {
            int x = ope[i].x;
            if (S.find(x) == S.end()) S.insert(x);
            vec[x].push_back(i);
        }
        else if (ope[i].opt == 2) {
            int l = ope[i].l, r = ope[i].r, v = ope[i].x;
            while (true) {
                it = S.lower_bound(l);
                if (it == S.end() || (*it) > r) break;
                for (auto &t : vec[*it]) {
                    add(t, v);
                }
                vec[*it].clear();
                S.erase(it);
            }
        }
        else {
            int x = ope[i].l, y = ope[i].r;
            if (x != y) {
                if (S.find(x) != S.end()) S.erase(x);
                if (S.find(y) != S.end()) S.erase(y);
                swap(vec[x], vec[y]);
                if (vec[x].size()) S.insert(x);
                if (vec[y].size()) S.insert(y);
            }
        }

        for (auto &p : query[i]) {
            ans[p.second] = sum(p.first);
        }
    }
    for (int i = 1; i <= Q; ++ i) {
        printf("%lld\n", ans[i]);
    }
    return 0;
}