Interstellar 题解

一、题目：

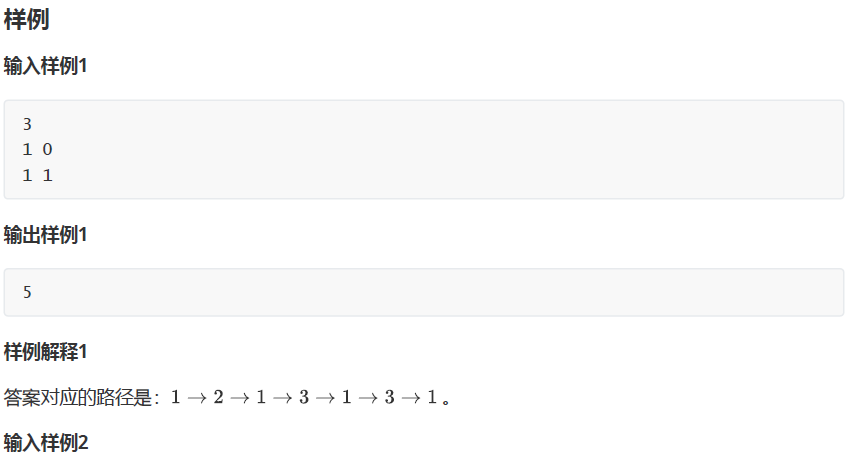
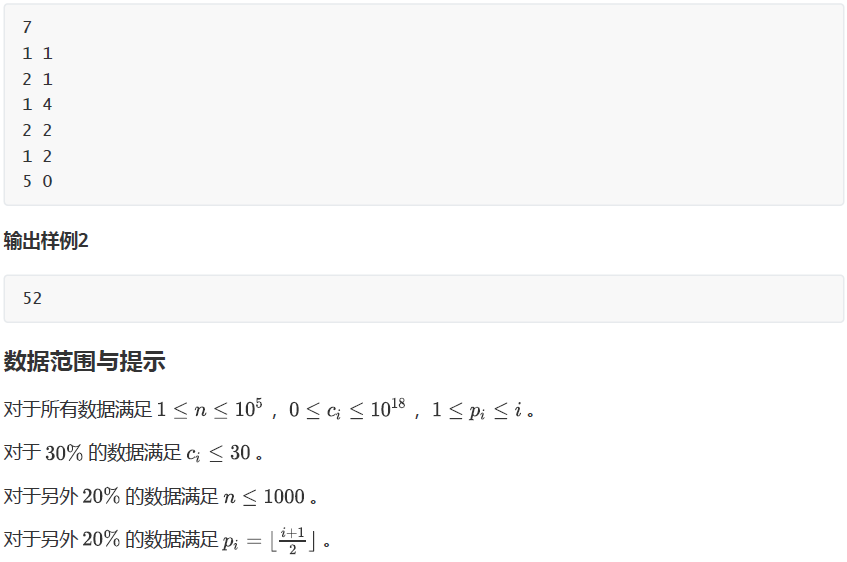
二、思路：

在没看数据范围之前，这道题有一个十分显然的树形DP做法。

设 \(dp(x)\) 表示 \(x\) 及其子树内所能获得的最大代价（题目为什么要使代价最大化呢？），于是有转移方程

\[dp(x)=\max_{y\in son(x)}\{dp(y)+w(x,y)\}+\sum_{y\in son(x)} (dp(y)+w(x,y)) \]

时间复杂度 \(O(n)\)，这题不就解决了吗？

然后看到数据范围 \(0\leq c_i\leq 10^{18}\)，也就是说每条边的权值最大可以是 \(2^{10^{18}}\)，当场去世。

于是考虑用 set 维护每条边的权值中有哪几个2的幂次。加法和比较大小都类似于高精度。

考虑这样的复杂度为什么是对的，因为每条边至多只会贡献一个2的幂次，而且加法每进一位都会少一个1，所以每次均摊复杂度是 \(O(1)\) 的。如果我们再用启发式合并，那总的复杂度就是 \(O(n\log^2 n)\)的。比较大小也一样。

再考虑我们还要取出最大的数进行累加，这时候相当于对一个数乘2，也就是每一个2的幂次都会左移。暴力移肯定不行，考虑使用懒标记。

然后呢？然后就没了。

三、启示：

其实这样的做法很容易想到，这启发我们需要认真分析复杂度，而且当不方便实时维护的时候一定要想到懒标记，有时候能解决很多问题。

四、代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <set>

using namespace std;

#define FILEIN(s) freopen(s".in", "r", stdin)
#define FILEOUT(s) freopen(s".out", "w", stdout)

inline long long read(void) {
    long long x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int maxn = 1e5 + 5, mod = 998244353;

int n, tot = 1, head[maxn];
long long ans[maxn];

struct Edge {
    int y, next;
    long long w;
    Edge() {}
    Edge(int _y, int _next, long long _w) : y(_y), next(_next), w(_w) {}
}e[maxn << 1];

struct Node {
    set<long long>S;
    long long tag;
    inline void insert(long long p) {
        p -= tag;
        while (S.find(p) != S.end()) {
            S.erase(p);
            ++ p;
        }
        S.insert(p);
    }
    inline friend bool operator <(const Node&a, const Node&b) {
        if (b.S.size() == 0) return 0;
        if (a.S.size() == 0) return 1;
        set<long long>::iterator i1 = a.S.end(), i2 = b.S.end();
        -- i1; -- i2;
        while ((*i1) + a.tag == (*i2) + b.tag) {
            if (i2 == b.S.begin()) return 0;
            if (i1 == a.S.begin()) return 1;
            -- i1; -- i2;
        }
        return (*i1) + a.tag < (*i2) + b.tag;
    }
}dp[maxn];

inline long long power(long long a, long long b) {
    long long res = 1;
    for (; b; b >>= 1) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}

inline void connect(int x, int y, long long w) {
    e[++ tot] = Edge(y, head[x], w);
    head[x] = tot;
}

void dfs(int x, int fa) {
    int mx = -1;

    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].y;
        if (y == fa) continue;
        dfs(y, x);
        ans[y] += power(2, e[i].w);
        dp[y].insert(e[i].w);
        if (mx == -1 || dp[mx] < dp[y]) mx = y;
    }

    if (mx != -1) {
        ++ dp[mx].tag;
        (ans[mx] *= 2) %= mod;
    }

    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].y;
        if (y == fa) continue;

        if (dp[y].S.size() > dp[x].S.size()) swap(dp[y], dp[x]);

        for (set<long long>::iterator it = dp[y].S.begin(); it != dp[y].S.end(); ++ it) {
            dp[x].insert(*it + dp[y].tag);
        }

        (ans[x] += ans[y]) %= mod;
    }

}

int main() {
    FILEIN("a"); FILEOUT("a");
    n = read();
    for (int i = 1; i < n; ++ i) {
        int p = read(); long long w = read();
        connect(i + 1, p, w);
        connect(p, i + 1, w);
    }
    dfs(1, 0);
    printf("%lld\n", ans[1]);
    return 0;
}