洛谷 P4354 [CERC2015]Ice Igloos 题解

一、题目：

洛谷原题

codeforces原题

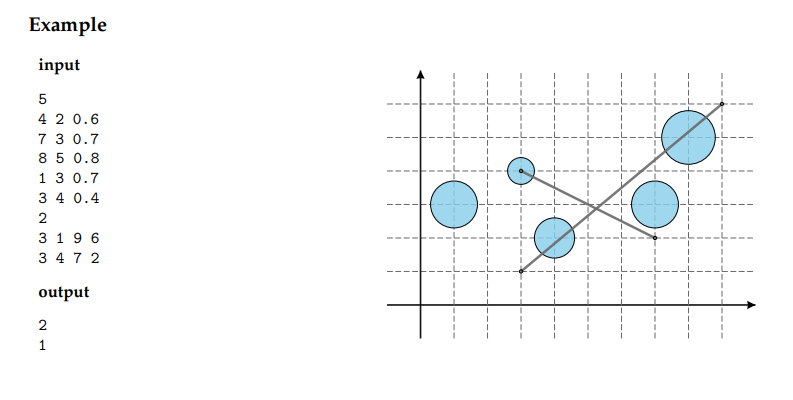
二、思路：

先考虑一个很朴素的想法，就是枚举\(500\times 500\)坐标系中的所有点，如果一个点\(P(x_0,y_0)\)上面存在着 igloo 就判断\(P\)到线段的距离是否小于 igloo 的半径，如果小于，那么就累计到答案中。时间复杂度\(O(q\times {maxx}^2)\)。

注意到题目中的一个重要性质，就是点的坐标都是整数，而且 igloo 的半径都很小。所以，可能产生贡献的点非常有限。即：只有与线段相距小于等于1的点才有可能产生贡献。所以我们只需把这些点找出来进行判断即可。时间复杂度\(O(q\times {maxx})\)。

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>

#define Vector Point
#define eps 1e-8

using namespace std;

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int maxx = 505;

int n, Q;

double radius[maxx][maxx];

inline int sign(double a) {
    if (a < -eps) return -1;
    if (a > eps) return 1;
    return 0;
}

struct Point {
    double x, y;
    Point() {}
    Point(double _x, double _y) : x(_x), y(_y) {}
    inline friend bool operator == (const Point&a, const Point&b) {
        return sign(a.x - b.x) == 0 && sign(a.y - b.y) == 0;
    }
    inline friend Point operator - (const Point&a, const Point&b) {
        return Point(a.x - b.x, a.y - b.y);
    }
};

inline double get_length(Point a) {
    return sqrt(a.x * a.x + a.y * a.y);
}

inline double dot(Vector a, Vector b) {
    return a.x * b.x + a.y * b.y;
}

inline double cross(Vector a, Vector b) {
    return a.x * b.y - b.x * a.y;
}

inline double distance_to_line(Point p, Point a, Point b) {
    Vector v1 = b - a, v2 = p - a;
    return fabs(cross(v1, v2) / get_length(v1));
}

inline double distance_to_segment(Point p, Point a, Point b) {
    if (a == b) return get_length(p - a);
    Vector v1 = b - a, v2 = p - a, v3 = p - b;
    if (sign(dot(v1, v2)) < 0) return get_length(v2);
    if (sign(dot(v1, v3)) > 0) return get_length(v3);
    return distance_to_line(p, a, b);
}

inline void work3(int x1, int y1, int x2, int y2) {
    if (x1 > x2) swap(x1, x2), swap(y1, y2);
    double k = 1.0 * (y2 - y1) / (x2 - x1);
    int dy = sqrt(k * k + 1) + 2, cnt = 0;
    for (int i = x1; i <= x2; ++i) {
        int y = (i - x1) * k + y1;
        for (int j = max(y - dy, 1); j <= min(y + dy, 500); ++j) {
            if (radius[i][j] > 0 && sign(distance_to_segment(Point(i, j), Point(x1, y1), Point(x2, y2)) - radius[i][j]) < 0)
                ++cnt;
        }
    }
    printf("%d\n", cnt);
}

inline void work1(int x1, int x2, int y) {
    if (x1 > x2) swap(x1, x2);
    int cnt = 0;
    for (int i = x1; i <= x2; ++i) {
        if (radius[i][y] > 0) ++cnt;
    }
    printf("%d\n", cnt);
}

inline void work2(int y1, int y2, int x) {
    if (y1 > y2) swap(y1, y2);
    int cnt = 0;
    for (int j = y1; j <= y2; ++j) {
        if (radius[x][j] > 0) ++cnt;
    }
    printf("%d\n", cnt);
}

int main() {
    n = read();
    for (int i = 1; i <= n; ++i) {
        int x = read(), y = read();
        scanf("%lf", &radius[x][y]);
    }
    Q = read();
    while (Q--) {
        int x1 = read(), y1 = read(), x2 = read(), y2 = read();
        if (y1 == y2) { // horizontal
            work1(x1, x2, y1);
        }
        else if (x1 == x2) { // vertical
            work2(y1, y2, x1);
        }
        else work3(x1, y1, x2, y2);
    }
    return 0;
}