洛谷 P4609 [FJOI2016]建筑师 题解

一、题目：

洛谷原题

二、思路：

考虑将高度为\(n\)的建筑加入到高度为\(1\sim n-1\)的建筑群中。

为了易于描述，我们将高度为\(i\)的建筑编号为\(i\)。

容易发现，第\(n\)个建筑左边应该会有\(A-1\)个建筑可以看到，第\(n\)个建筑右边应该会有\(B-1\)个建筑可以看到。

看一下这张图：

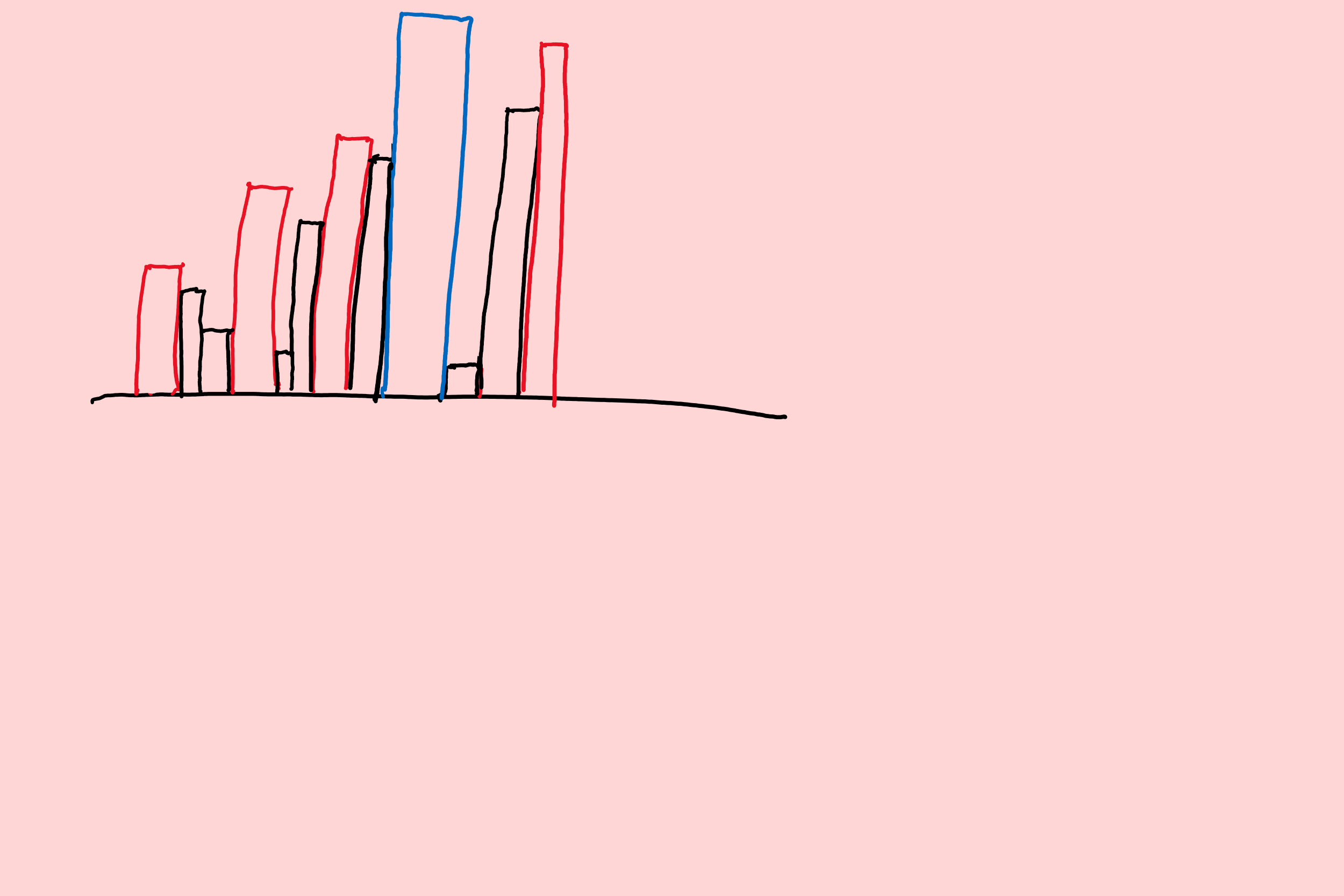
我们发现，每一个红色的的建筑都会挡住一些黑色的建筑。所以，如果我们把每一个红色的建筑与被它挡住的黑色的建筑归为一类的话，那么原问题就可以描述为将\(n-1\)个建筑划分为\(A+B-2\)个圆排列，那么这显然是第一类 Stirling 数\(s(n-1,A+B-2)\)。

但是这还没有完，我们还要从这\(A+B-2\)个组中挑出\(A-1\)个放到蓝色建筑（也就是第\(n\)个建筑）的左边，挑出\(B-1\)个放到蓝色建筑的右边，这对应着组合数\(\dbinom{A+B-2}{A-1}\)。

有些朋友可能会问，当把一些组选出来放到左边（或右边）后，不用再考虑组的放置顺序吗？答案是否定的。原因是因为要想保证这几个组的红色建筑都能被看到，那么这些组一定是按照红色建筑递增（或递减）的顺序排好序了，因此顺序只有唯一的一种。

所以最终的方案数就是\(s(n-1,A+B-2)\times \dbinom{A+B-2}{A-1}\)。

递推求解第一类 Stirling 数以及组合数即可。

\(s(p,0)=0,p\geq 1\)

\(s(p,p)=1,p\geq 0\)

\(s(p,k)=s(p-1,k-1)+(p-1)\times s(p-1,k),1\leq k< p\)

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;
inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int maxn = 50005, maxA = 105, mod = 1e9 + 7;

int T;

int s[maxn][maxA << 1], C[maxA << 1][maxA << 1];

inline void init(void) {
    s[0][0] = 1;
    for (int p = 1; p <= 50000; ++ p) {
        s[p][0] = 0;
        if (p <= 200) s[p][p] = 1;
        for (int k = 1; k < min(p, 200); ++ k) {
            s[p][k] = s[p - 1][k - 1] + 1LL * (p - 1) * s[p - 1][k] % mod;
            s[p][k] %= mod;
        }
    }
    C[0][0] = 1;
    for (int i = 1; i <= 200; ++ i) {
        C[i][0] = 1;
        C[i][i] = 1;
        for (int j = 1; j < i; ++ j) {
            C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % mod;
        }
    }
}

int main() {
    init();
    T = read();
    while (T --) {
        int n = read(), A = read(), B = read();
        int res = 1LL * s[n - 1][A + B - 2] * C[A + B - 2][A - 1] % mod;
        printf("%d\n", res);
    }
    return 0;
}