图 题解

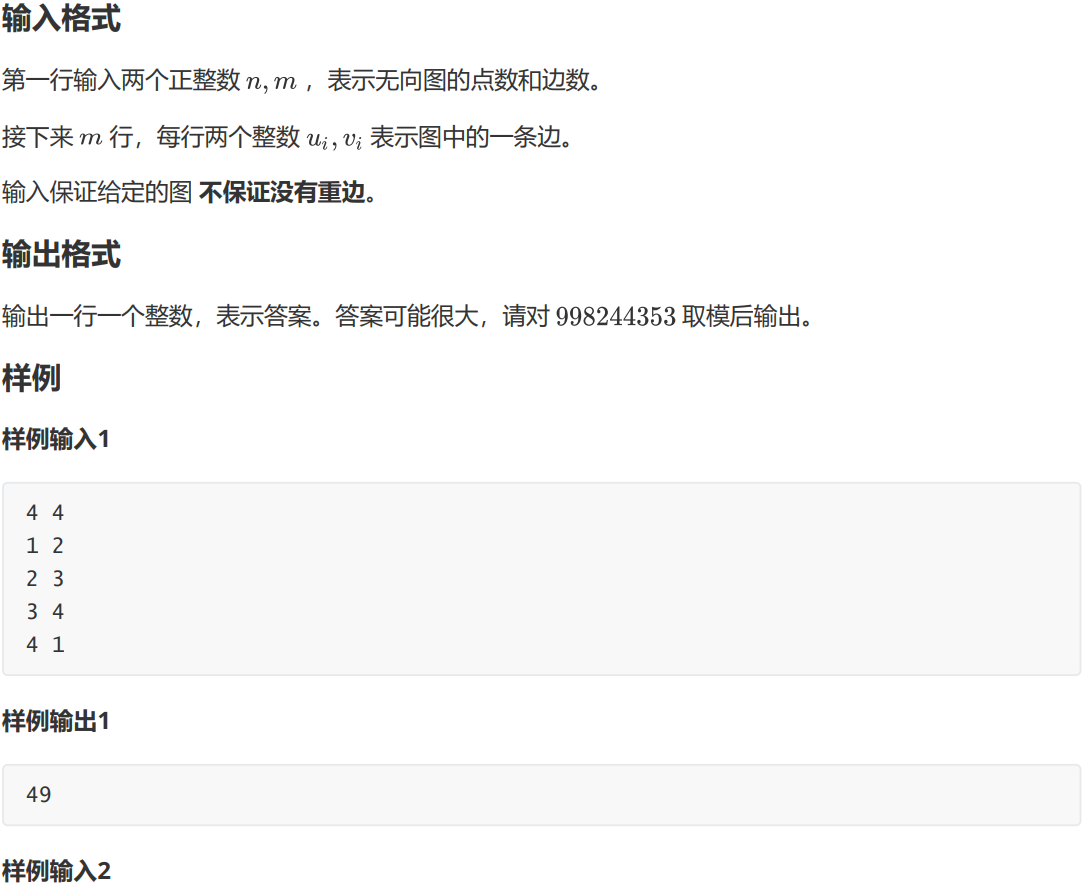
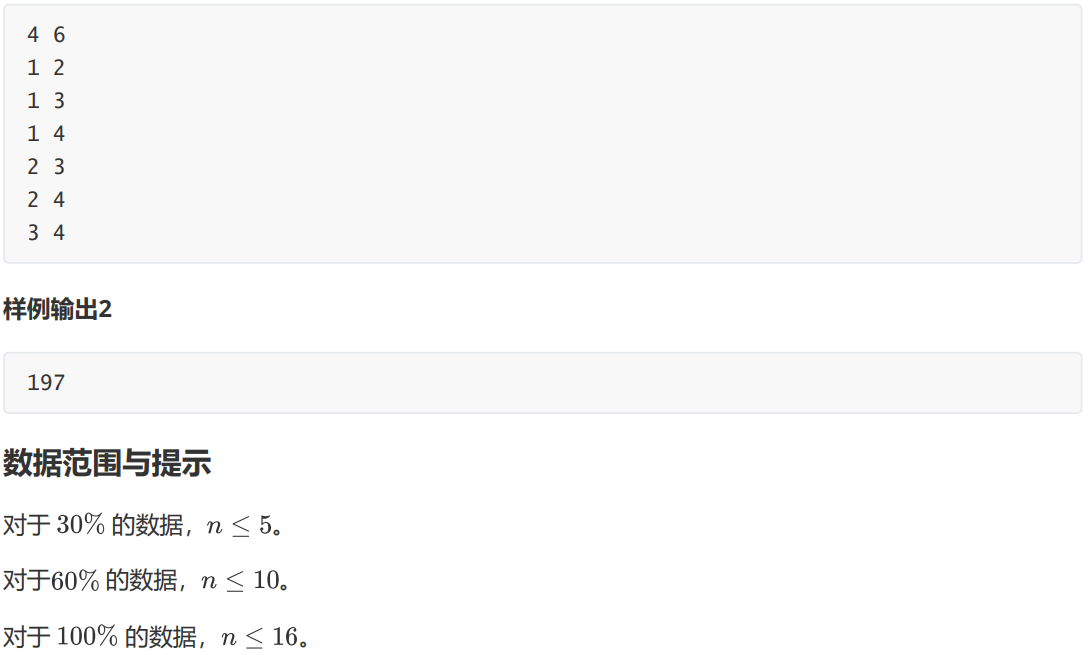
一、题目：

二、思路：

容易看出，本题的意思是说，保留一张图的一些边，图就会被分割成很多个联通块。新的图至多只能有一个环。每种情况的贡献是所有联通块大小的乘积。

我们首先可以用这道题的思路，预处理出\(circle(s)\)，表示由\(s\)这个集合中的点可以组成几个环。

考虑\(O(2^n)\)枚举当前要保留哪个环。设当前环中的所有点的集合是\(s\)。将\(s\)缩点，设缩成的大点是\(S\)。建立一个虚拟节点\(T\)，从虚拟节点向剩下的每个节点连一条无向边。特别地，从\(T\)向\(S\)连\(|s|\)条边。

然后，用矩阵树定理处理出当前图的生成树个数。然后我们惊奇地发现，当前图的生成树个数就等于所有可能的联通块大小之积的总和。这个很容易证明，用映射的思想想一想就可以发现它是对的。重点是需要记住这一个重要的转化。

然后别忘了乘上形成\(s\)环的方案数。

所以矩阵树定理+状压DP即可解决本题。

三、代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <ctime>

#define FILEIN(s) freopen(s".in", "r", stdin)
#define FILEOUT(s) freopen(s".out", "w", stdout)
#define mem(s, v) memset(s, v, sizeof s)

using namespace std;

inline int read(void) {
    int x = 0, f = 1; char ch = getchar();
    while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
    while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
    return f * x;
}

const int maxn = 18, mod = 998244353;

int n, m;

long long circle[1 << maxn], f[maxn][1 << maxn];
long long mat[maxn][maxn], ans;

int G[maxn][maxn];

#define call(s, i) ((s >> i) & 1)

inline int lowbit(int x) { return x & (-x); }

inline int count(int s) {
    int res = 0;
    for (int i = 0; i < n; ++ i) {
        if (call(s, i)) ++ res;
    }
    return res;
}

inline long long power(long long a, long long b) {
    long long res = 1;
    for (; b; b >>= 1) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
    }
    return res;
}

inline void init(void) {
    for (int x = 0; x < n; ++ x) f[x][1 << x] = 1;
    for (int s = 0; s < (1 << n); ++ s) {
        for (int x = 0; x < n; ++ x) {
            if (!call(s, x)) continue;
            for (int y = 0; y < n; ++ y) {
                if (!G[x][y]) continue;
                if (lowbit(s) > (1 << y)) continue;
                if (lowbit(s) == (1 << y)) (circle[s] += f[x][s]) %= mod;
                else if (!call(s, y)) (f[y][s | (1 << y)] += f[x][s]) %= mod;
            }
        }
    }
    for (int s = 0; s < (1 << n); ++ s) {
        if (count(s) <= 2) circle[s] = 0;
        else (circle[s] *= (mod + 1) / 2) %= mod;
    }
}

inline long long Gauss(long long a[maxn][maxn], int n) {
    long long res = 1;
    for (int i = 0; i < n; ++ i) {
        int mx = i;
        for (int j = i; j < n; ++ j) {
            if (a[j][i] != 0) { mx = j; break; }
        }
        if (!a[mx][i]) return 0;
        if (mx != i) swap(a[mx], a[i]), res = -res;
        for (int j = i + 1; j < n; ++ j) {
            long long r = a[j][i] * power(a[i][i], mod - 2) % mod;
            for (int k = i; k < n; ++ k) {
                (a[j][k] -= r * a[i][k] % mod) %= mod;
            }
        }
    }
    for (int i = 0; i < n; ++ i) {
        (res *= a[i][i]) %= mod;
    }
    if (res < 0) res += mod;
    return res;
}

inline void prepare(int s) {
    mem(mat, 0);
    int represent = log2(lowbit(s));
    for (int x = 0; x < n; ++ x) {
        for (int y = 0; y < n; ++ y) {
            if (call(s, x) && call(s, y)) continue;
            if (call(s, x) && !call(s, y))
                (mat[represent][y] -= G[x][y]) %= mod,
                (mat[represent][represent] += G[x][y]) %= mod;
            if (!call(s, x) && call(s, y))
                (mat[x][represent] -= G[x][y]) %= mod,
                (mat[x][x] += G[x][y] % mod) %= mod;
            if (!call(s, x) && !call(s, y))
                (mat[x][y] -= G[x][y]) %= mod,
                (mat[x][x] += G[x][y]) %= mod;
        }
    }
    for (int x = 0; x < n; ++ x) {
        if (x == represent) {
            int cnt = count(s);
            mat[x][n] -= cnt % mod;
            mat[x][n] %= mod;
            mat[n][x] -= cnt % mod;
            mat[n][x] %= mod;
            mat[x][x] += cnt % mod;
            mat[x][x] %= mod;
            mat[n][n] += cnt % mod;
            mat[n][n] %= mod;
        } else {
            mat[x][n] --;
            mat[n][x] --;
            mat[x][x] ++;
            mat[n][n] ++;
        }
    }
}

int main() {
    FILEIN("graph"); FILEOUT("graph");
    n = read(); m = read();
    for (int i = 1; i <= m; ++ i) {
        int x = read(), y = read();
        -- x; -- y;
        G[x][y] = G[y][x] = 1;
    }
    init();
    for (int x = 0; x < n; ++ x)
        for (int y = 0; y < n; ++ y) {
            mat[x][y] -= G[x][y];
            mat[x][x] += G[x][y];
        }
    for (int x = 0; x < n; ++ x) {
        -- mat[x][n];
        -- mat[n][x];
        ++ mat[x][x];
        ++ mat[n][n];
    }
    (ans += Gauss(mat, n)) %= mod;
    for (int s = 0; s < (1 << n); ++ s) {
        if (count(s) <= 2) continue;
        if (!circle[s]) continue;
        prepare(s);
        (ans += Gauss(mat, n) * circle[s]) %= mod;
    }
    printf("%lld\n", ans);
    return 0;
}