点对游戏 题解
一、题目:
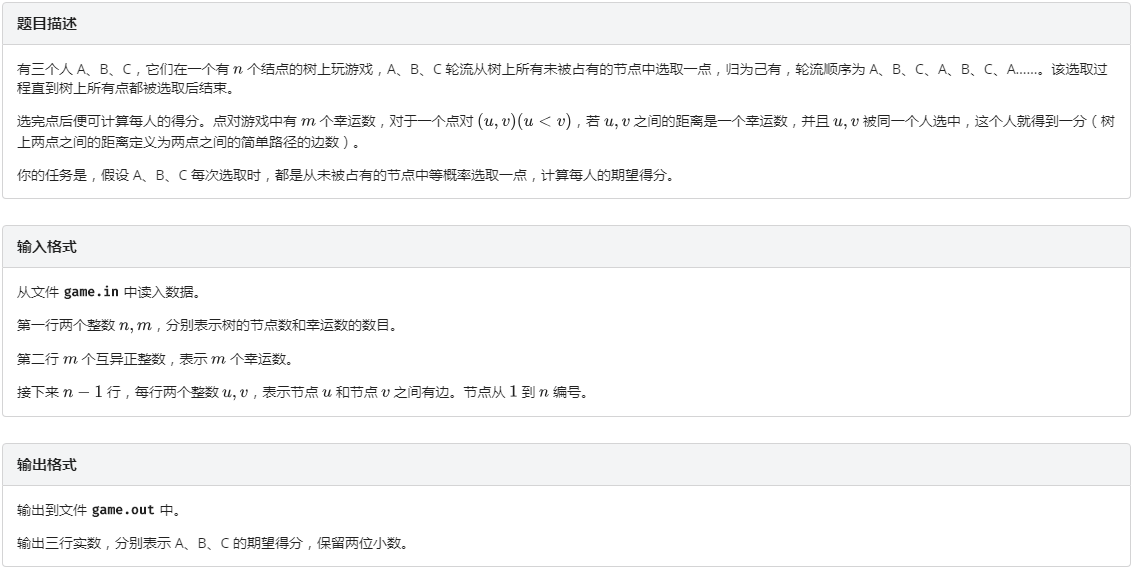
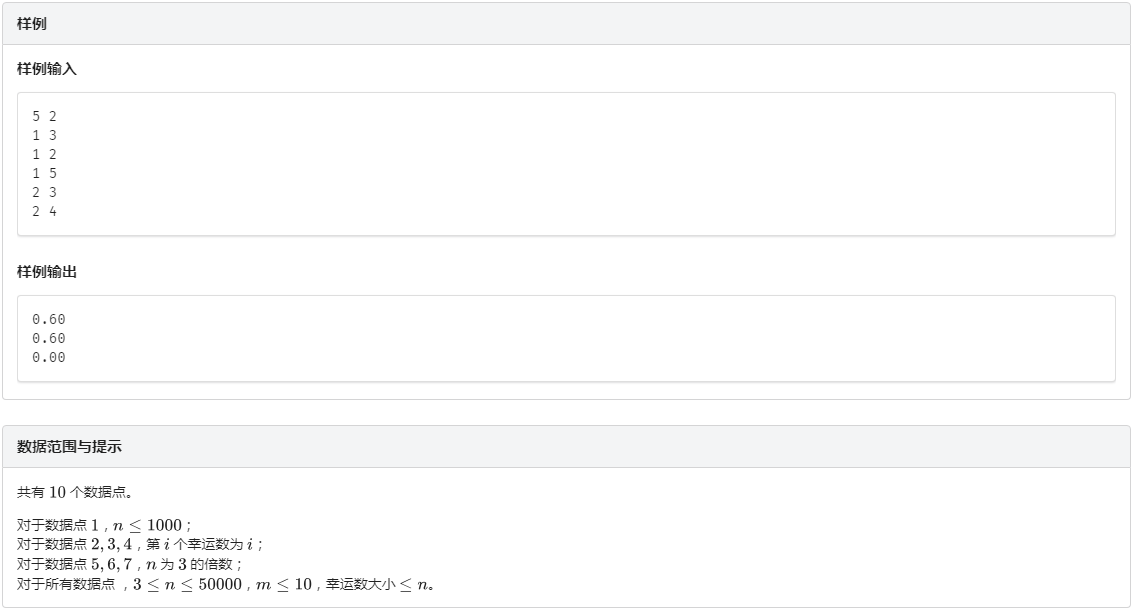
二、思路:
这道题相对来说比较简单,主要考察对于期望的深刻理解。
其实,我是属于那种对数学期望一窍不通的人。我个人感觉做期望题可以从以下三个方面入手:
- 考虑每个元素对答案的贡献。比如说你做一份卷子,只有25道选择题,一道题4分,每道题蒙对的概率是\(\dfrac{1}{4}\)(假设你和我一样是个啥都不会的菜鸡,只能蒙题),那么一道题对于期望的贡献就是\(4\times \dfrac{1}{4}=1\),所以你的期望得分就是25分。并不需要将每种情况列出来,算每种情况的概率乘得分,也就是说不需要像高中数学大题一样求分布列。
- 把“期望”理解为“估摸”,这一种思考方式常用于期望DP。比如给一张有向无环图和起点\(S\)和终点\(T\),开始你站在起点,每次等概率的往下走,问走到终点的期望步数。那么\(dp(u)\)表示走到从\(u\)走到\(T\)的期望步数。那么我们就把它理解成从\(u\)走到\(T\)“估摸着”走\(dp(u)\)步。状态转移方程也就不难列出。
- 对于那种有后效性的题,不能用期望DP,就只能使用高斯消元。一般这样考虑,先求出点的期望,用点的期望再去求出边的期望。
对于本题来说,我们发现A、B、C三个人取点的顺序是无所谓的。这就好比是教室里同学们抽签,谁先抽都无所谓,抽到的概率都一样。
我们设\(cnt\)为距离为幸运数的点对个数,设\(k\)为某个人一共要取的点的个数。那么这个人的答案:\(\dfrac{C_{n-2}^{k-2}}{C_n^k}\times cnt=\dfrac{\dfrac{(n-2)!}{(k-2)!\times (n-k)!}}{\dfrac{n!}{k!\times (n-k)!}}\times cnt=\dfrac{k\times (k-1)}{n\times (n-1)}\times cnt\)。
至于\(cnt\)怎么求,点分治模板题。
三、代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define FILEIN(s) freopen(s".in", "r", stdin)
#define FILEOUT(s) freopen(s".out", "w", stdout)
inline int read(void) {
int x = 0, f = 1; char ch = getchar();
while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
return f * x;
}
const int maxm = 15, maxn = 50005;
int n, m, lucky[maxm], head[maxn], tot = 1;
int p[maxn], q[maxn], ans;
bool vis[maxn];
struct Edge {
int y, next;
Edge() {}
Edge(int _y, int _next) : y(_y), next(_next) {}
} e[maxn << 1];
inline void connect(int x, int y) {
e[++ tot] = Edge(y, head[x]);
head[x] = tot;
}
inline int get_size(int x, int fa) {
if (vis[x]) return 0;
int res = 1;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].y;
if (y == fa) continue;
res += get_size(y, x);
}
return res;
}
inline int get_wc(int x, int fa, int tot_size, int &wc) {
if (vis[x]) return 0;
int res = 1, mx = 0;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].y;
if (y == fa) continue;
int tmp = get_wc(y, x, tot_size, wc);
mx = max(mx, tmp);
res += tmp;
}
mx = max(mx, tot_size - res);
if (mx * 2 <= tot_size) wc = x;
return res;
}
void get_dist(int x, int fa, int dist, int &nq) {
if (vis[x]) return;
q[++ nq] = dist;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].y;
if (y == fa) continue;
get_dist(y, x, dist + 1, nq);
}
}
inline void count(int a[], int len, int k, int t) {
sort(a + 1, a + len + 1);
for (int r = len, l1 = 0, l2 = 0; r >= 1; -- r) {
while (true) {
if (l1 + 1 < r && a[l1 + 1] + a[r] <= k) ++ l1;
else break;
}
while (true) {
if (l2 + 1 < r && a[l2 + 1] + a[r] <= k - 1) ++ l2;
else break;
}
l1 = min(l1, r - 1);
l2 = min(l2, r - 1);
ans += (l1 - l2) * t;
}
}
void solve(int x) {
if(vis[x]) return;
get_wc(x, 0, get_size(x, 0), x);
vis[x] = true;
int np = 0;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].y;
int nq = 0;
get_dist(y, x, 1, nq);
for (int j = 1; j <= m; ++ j) {
count(q, nq, lucky[j], -1);
for (int k = 1; k <= nq; ++ k) {
if (q[k] == lucky[j]) ++ ans;
}
}
for (int j = 1; j <= nq; ++ j) p[++ np] = q[j];
}
for (int j = 1; j <= m; ++ j) {
count(p, np, lucky[j], 1);
}
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].y;
solve(y);
}
}
inline long double calc(int k) {
long double res = 1.0;
res = res * k * (k - 1) * ans / n / (n - 1);
return res;
}
int main() {
FILEIN("game"); FILEOUT("game");
n = read(); m = read();
for (int i = 1; i <= m; ++ i) {
lucky[i] = read();
}
for (int i = 1; i < n; ++ i) {
int x = read(), y = read();
connect(x, y); connect(y, x);
}
solve(1);
int k3 = n / 3, k2, k1;
if (n % 3 == 0) k2 = k1 = k3;
if (n % 3 == 1) k2 = k3, k1 = k2 + 1;
if (n % 3 == 2) k2 = k3 + 1, k1 = k2;
printf("%.2Lf\n%.2Lf\n%.2Lf\n", calc(k1), calc(k2), calc(k3));
return 0;
}

