值域连续 题解

一、题目：

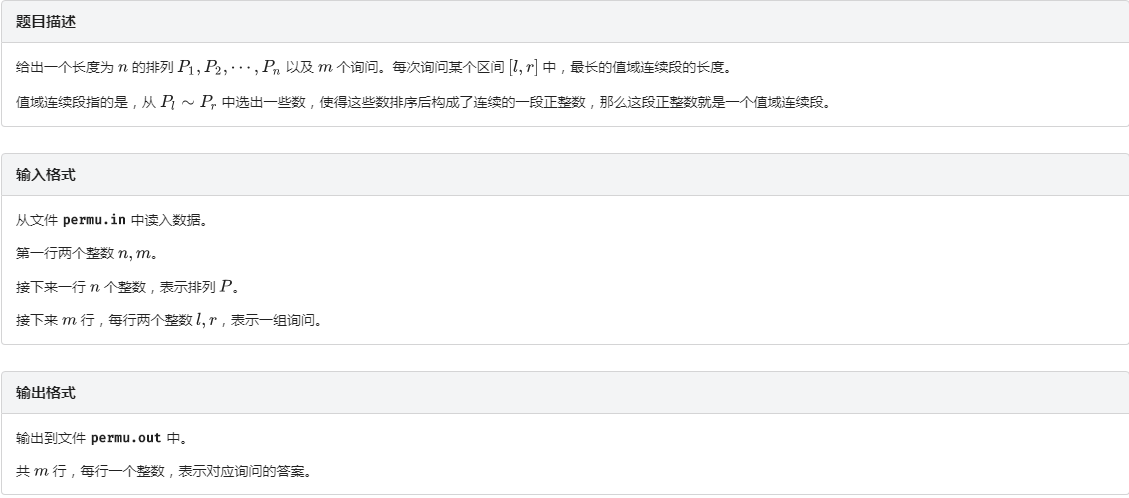
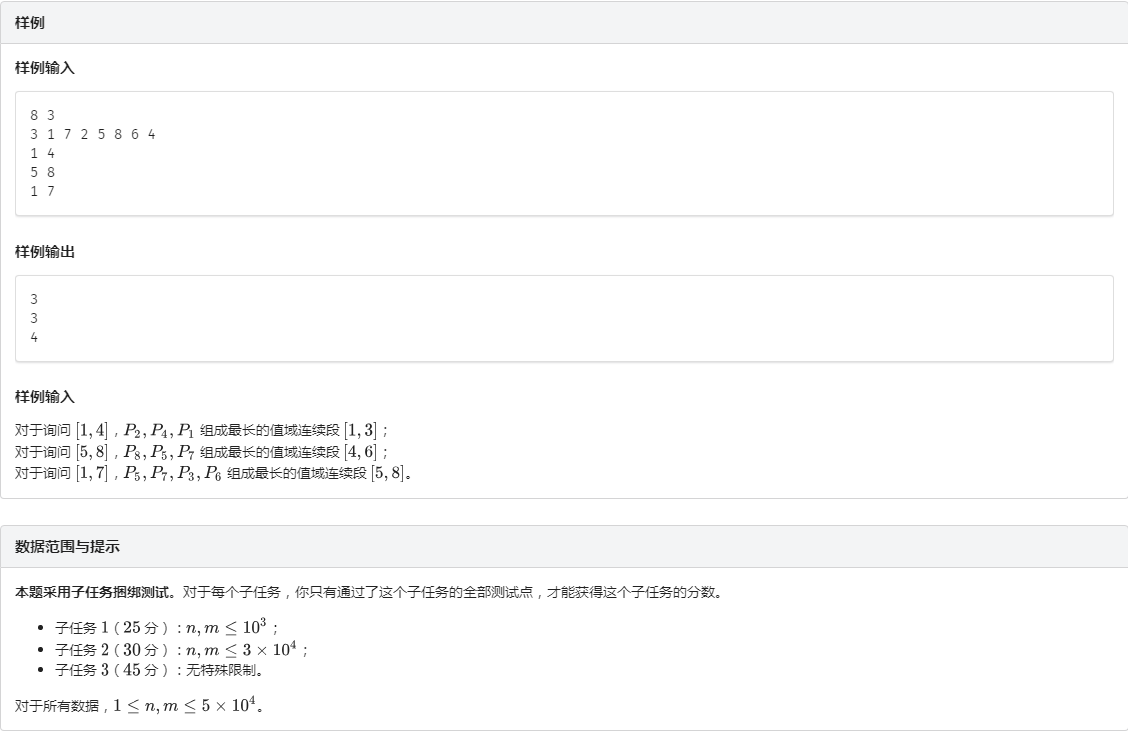
二、思路：

首先我们发现这道题的一些美妙的性质：离线、不带修改（静态）、数据范围较小。这些性质促使我们联想到一种神奇的算法：莫队。

那么普通的莫队是无法处理这种最大值的情况的。于是我们引入“回滚莫队”算法。在这里简单介绍一下。

回滚莫队本质上就是考虑能不能使得莫队区间的移动操作只有“增加”，没有“减少”。具体的做法是这样的。

首先排序和普通的莫队一样，第一关键字是左端点所在块的编号，第二关键字是右端点。

然后考虑对于一个块\(b\)以及左端点在这个块中的所有区间\(S=\{(l, r) | l \in b\}\)，我们将这些区间分成两类。第一类\(S_1\)是右端点也都在\(b\)中的区间，第二类\(S_2\)是右端点不在\(b\)中的区间。

对于\(S_1\)中的所有询问，暴力扫描。

对于\(S_2\)中的询问，初始的时候记\(L = r_b+1,R = r_b\)（\(r_b\)表示块\(b\)的右端点）。每次扫描到\(S_2\)中的一个询问\((l,r)\)，将\(L\)移动至\(l\)，将\(R\)移动至\(r\)，记录该区间的答案。最后将\(L\)重新移动回\(r_b+1\)，并撤销由于\(L\)移动带来的影响。

这样，我们就能保证每次移动指针\(L,R\)，都是“只增不减”的。

对于本题来说，我们可以用并查集维护值域上的连续性。

做完了吗？并没有。

我们发现并查集很难进行“撤销”操作。当然，“难“的前提是使用了”路径压缩“优化，导致树的形态不断发生变化。

所以我们考虑不用“路径压缩”，使用“按秩合并”优化。每次用栈记录并查集树中的哪些节点被改变过，“撤销”的时候依次从栈中弹出每个元素进行撤销即可。

时间复杂度\(O(n\sqrt n\log_2 n)\)。

三、代码：

//写得较为丑陋
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <stack>

using namespace std;

#define LL long long
#define mem(s, v) memset(s, v, sizeof s)

inline int read(void) {
	int x = 0, f = 1; char ch = getchar();
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return f * x;
}

const int maxn = 5e4 + 5;

int n, m, a[maxn], len, tot;

int bll[maxn], blr[maxn], mx;

int siz[maxn], fa[maxn], ans[maxn];

int lasmx;

bool tag[maxn];

stack<int>st;

struct Query {
	int l, r, id;
	inline friend bool operator < (Query x, Query y) {
		if (x.l / len != y.l / len) return x.l / len < y.l / len;
		return x.r < y.r;
	}
}q[maxn];

inline int find(int x) {
	if (x == fa[x]) return x;
	return find(fa[x]);
}

inline void merge(int x, int y) {
	x = find(x); y = find(y);
	if (x == y) return;
	if (siz[x] > siz[y]) swap(x, y);
	fa[x] = y;
	siz[y] += siz[x];
	st.push(x);
}

inline void add(int p) {
	tag[p] = 1;
	if (tag[p + 1]) merge(p, p + 1);
	if (tag[p - 1]) merge(p, p - 1);
	mx = max(mx, siz[find(p)]);
}

int main() {
	freopen("permu.in", "r", stdin);
	freopen("permu.out", "w", stdout);
	n = read(); m = read();
	len = sqrt(n);
	for (int i = 1; i <= n; ++ i) a[i] = read();
	for (int i = 1; i <= m; ++ i) {
		q[i].l = read(); q[i].r = read();
		q[i].id = i;
	}
	sort(q + 1, q + m + 1); tot = q[m].l / len;
	mem(bll, 0x3f);
	for (int i = 1; i <= m; ++ i) {
		bll[q[i].l / len] = min(bll[q[i].l / len], i);
		blr[q[i].l / len] = i;
	}
	for (int bl = 0; bl <= tot; ++ bl) {
		for (int i = 1; i <= n; ++ i) fa[i] = i, siz[i] = 1, tag[i] = 0;
		while (st.size()) st.pop();
		lasmx = 0;

		int i;
		for (i = bll[bl]; i <= blr[bl] && q[i].r <= len * (bl + 1) - 1; ++ i) {
			while (st.size()) {
				int x = st.top(); st.pop();
				siz[fa[x]] -= siz[x];
				fa[x] = x;
			}

			mx = 0;
			for (int j = q[i].l; j <= q[i].r; ++ j) {
				add(a[j]);
			}
			ans[q[i].id] = mx;

			for (int j = q[i].l; j <= q[i].r; ++ j) tag[a[j]] = 0;
		}
        int L = len * (bl + 1), R = L - 1, cnt = 0;
		for (; i <= blr[bl]; ++ i) {

			mx = lasmx;
			while ((int)st.size() > cnt) {
				int x = st.top(); st.pop();
				siz[fa[x]] -= siz[x];
				fa[x] = x;
			}
			while (L < len * (bl + 1)) tag[a[L ++]] = 0;
			while (R < q[i].r) add(a[++ R]);
			cnt = st.size();
			lasmx = mx;
			while (L > q[i].l) add(a[-- L]);
			ans[q[i].id] = mx;
		}
	}
    for (int i = 1; i <= m; ++ i)
        printf("%d\n", ans[i]);
	return 0;
}