【转】后缀数组一·重复旋律 题解
一、题目:
- 样例输入
-
8 2 1 2 3 2 3 2 3 1
- 样例输出
-
4
描述
小Hi平时的一大兴趣爱好就是演奏钢琴。我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。
小Hi在练习过很多曲子以后发现很多作品自身包含一样的旋律。旋律是一段连续的数列,相似的旋律在原数列可重叠。比如在1 2 3 2 3 2 1 中 2 3 2 出现了两次。
小Hi想知道一段旋律中出现次数至少为K次的旋律最长是多少?
输入
第一行两个整数 N和K。1≤N≤20000 1≤K≤N
接下来有 N 个整数,表示每个音的数字。1≤数字≤100
输出
一行一个整数,表示答案。
二、思路:
小Ho:这一次的问题该如何解决呢?
小Hi:嗯,这次的问题被称为最长可重叠重复K次子串问题。
小Ho:那一定是一个经典问题咯?
小Hi:没错!这个问题可以用后缀数组完美解决!
小Ho:后缀数组?我怎么没听说过!
小Hi:没事。且等我慢慢讲来!
小Ho:猴!
小Hi:顾名思义,后缀数组就是记录所有后缀的数组,同时,它也是有序的。后缀数组 SA 可以帮助我们解决单字符串问题、两个字符串的问题和多个字符串的问题等。
比如说字符串banana$,我们暂且把$认为是一个字符(表示字符串结尾)。我们记suffix(i)表示从原字符串第i个字符开始到字符串结尾的后缀。我们把它所有的后缀拿出来按字典序排序:
| 后缀 | i |
|---|---|
| $ | 7 |
| a$ | 6 |
| ana$ | 4 |
| anana$ | 2 |
| banana$ | 1 |
| na$ | 5 |
| nana$ | 3 |
并且我们把排好序的数组记做sa。比如sa[1]=7,sa[4]=2。
小Hi:这个我看懂了。
小Ho:对。另外,后缀数组会顺便记录名次数组 Rank, Rank[i] 保存的是后缀 i 在所有后缀中从小到大排列的“名次”。比如上个字符串中Rank[7]=1,Rank[4]=3
小Hi:那这和这个问题有什么关系呢?
小Ho:你别急嘛。我们现在令 height[i] 是 suffix(sa[i-1]) 和 suffix(sa[i]) 的最长公共前缀长度,即排名相邻的两个后缀的最长公共前缀长度。比如height[4]就是anana$和ana$的最长公共前缀,也就是ana,长度为3。你注意,这个height数组有一个神奇的性质:若 rank[j] < rank[k],则后缀 Sj..n 和 Sk..n 的最长公共前缀为 min{height[rank[j]+1],height[rank[j]+2]...height[rank[k]]}。这个性质是显然的,因为我们已经后缀按字典序排列。
小Hi:我想想……嗯,没错!
小Ho:好,假设我们现在已经求出了后缀数组,我们如何计算height呢?我们有如下结论:height[rank[i]] ≥ height[rank[i-1]]-1。
小Hi:这又是为什么?
小Ho:这个比较难理解。设suffix(k)是排在suffix(i-1)前一名的后缀,则它们的最长公共前缀是height[rank[i-1]]。那么suffix(k+1)将排在suffix(i)的前面(这里要求height[rank[i-1]]>1,如果height[rank[i-1]]≤1,原式显然成立)并且suffix(k+1)和suffix(i)的最长公共前缀是height[rank[i-1]]-1,所以suffix(i)和在它前一名的后缀的最长公共前缀至少是height[rank[i-1]]-1。你好好体会一下。
小Hi:嗯……我好好理解一下。
小Ho:别急,还没完,这样我们按照 height[rank[1]], height[rank[2]] ... height[rank[n]] 的顺序计算,利用height数组的性质,就可以将时间复杂度可以降为 O(n)。这是因为height数组的值最多不超过n,每次计算结束我们只会减1,所以总的运算不会超过2n次。
小Hi:哇!好神奇!
小Ho:有了height,求最长可重叠重复K次子串就方便了。重复子串即两后缀的公共前缀,最长重复子串,等价于两后缀的最长公共前缀的最大值。问题就转化成了,求height 数组中最大的长度为 K的子序列的最小值。
小Hi:哈哈!厉害!转化后的这个问题对我来说太容易了,利用单调队列或者二分都可以轻松搞定。
小Ho:等等!我还没说后缀数组怎么求呢!
小Hi:对哦。忘记这事了。
小Ho:后缀数组的求法有很多,最有名的是两种倍增算法和DC算法。时间复杂度上DC算法更优,但是很复杂。我们这里只介绍相对容易的倍增算法。
小Hi:好的。
小Ho:简单来说,倍增算法分以下四步
- 对长度为 20=1 的字符串,也就是所有单字母排序。
- 用长度为 20=1 的字符串,对长度为 21=2 的字符串进行双关键字排序。考虑到时间效率,我们一般用基数排序。
- 用长度为 2k-1 的字符串,对长度为 2k 的字符串进行双关键字排序。
- 直到 2k ≥ n,或者名次数组 Rank 已经从 1 排到 n,得到最终的后缀数组。
以字符串 "aabaaaab" 为例, 整个过程如图所示。 其中 x、 y 是表示长度为 2k 的字符串的两个关键字。
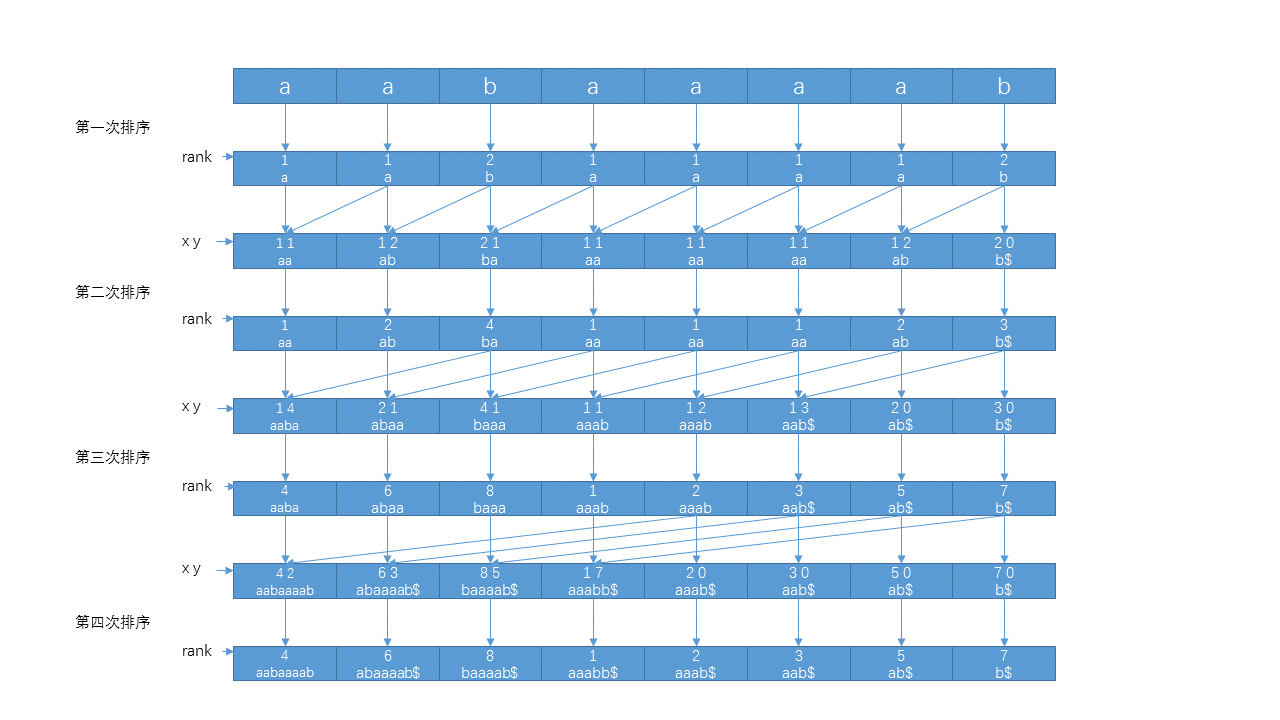
小Hi:我感觉这个算法就是利用已用的后缀排序信息来更新更长串的排序信息嘛!
小Ho:是有这个意思。我把c++代码打出来供你参考:
void solve()
{
for (int i = 0; i < 256; i ++) cntA[i] = 0;
for (int i = 1; i <= n; i ++) cntA[ch[i]] ++;
for (int i = 1; i < 256; i ++) cntA[i] += cntA[i - 1];
for (int i = n; i; i --) sa[cntA[ch[i]] --] = i;
rank[sa[1]] = 1;
for (int i = 2; i <= n; i ++)
{
rank[sa[i]] = rank[sa[i - 1]];
if (ch[sa[i]] != ch[sa[i - 1]]) rank[sa[i]] ++;
}
for (int l = 1; rank[sa[n]] < n; l <<= 1)
{
for (int i = 0; i <= n; i ++) cntA[i] = 0;
for (int i = 0; i <= n; i ++) cntB[i] = 0;
for (int i = 1; i <= n; i ++)
{
cntA[A[i] = rank[i]] ++;
cntB[B[i] = (i + l <= n) ? rank[i + l] : 0] ++;
}
for (int i = 1; i <= n; i ++) cntB[i] += cntB[i - 1];
for (int i = n; i; i --) tsa[cntB[B[i]] --] = i;
for (int i = 1; i <= n; i ++) cntA[i] += cntA[i - 1];
for (int i = n; i; i --) sa[cntA[A[tsa[i]]] --] = tsa[i];
rank[sa[1]] = 1;
for (int i = 2; i <= n; i ++)
{
rank[sa[i]] = rank[sa[i - 1]];
if (A[sa[i]] != A[sa[i - 1]] || B[sa[i]] != B[sa[i - 1]]) rank[sa[i]] ++;
}
}
for (int i = 1, j = 0; i <= n; i ++)
{
if (j) j --;
while (ch[i + j] == ch[sa[rank[i] - 1] + j]) j ++;
height[rank[i]] = j;
}
}
小Hi:我回去研究研究。尽快解决这个问题哈!


