MATLAB模拟布丰投针实验
MATLAB模拟布丰投针实验
标签(空格分隔): 算法
Buffon's Needle
桌面上有距离为a的若干平行线,将长度为L的针随机丢在桌面上,则这根针与平行线相交的概率是多少?假定L < a.
思路:从针据横线的距离与夹角得出。
解决:
- 假设针的中点到最近横线的距离为y,则\(y\in[0,\frac{a}{2}]\);
- 因为投针是随机的,所以y服从均匀分布:
\[ f(y) =
\begin{cases}
\frac{2}{a}, & \text{$0 \leq y \leq \frac{a}{2}$} \\
0, & \text{others}
\end{cases}
\]
- 假定横线向右为正向,记投针与横线正向的角为\(\theta\),则\(\theta \in[0, \pi]\),为均匀分布。
\[f(\theta) =
\begin{cases}
\frac{1}{\pi}, & \text{$0 \leq \theta \leq \pi$} \\
0, & \text{others}
\end{cases}
\]
投针与横线有交点,即\(y \leq \frac{L}{2}sin\theta\)
布丰投针估算\(\pi\) -- 蒙特卡罗模拟
针与横线有交点的概率:
\(P(x) = \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}f(y,\theta)dyd\theta = \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}f(y)f(\theta)dyd\theta \\
= \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}\frac{2}{a} * \frac{1}{\pi}dyd\theta = \frac{2L}{a\pi}\)
如果做n次投针实验,其中有k次针与横线相交,则针与横线相交的频率为:\(\frac{k}{n}\),根据大数定理,频率也就为概率。
$ \frac{2L}{a\pi} \approx \frac{k}{n}$ 即, \(\pi \approx \frac{2Ln}{ak}\)
MATLAB模拟实验
用布丰投针实验近似计算\(pi\)的值:
代码如下:
l = 0.6; %针的长度
a = 1; %平行线的宽度
n = 1000000; %做n次投针试验
k = 0; %记录针与平行线相交的次数
y = unifrnd(0, a/2, 1, n); %在[0, a/2]内服从均匀分布随机产生n个数
theta = unifrnd(0, pi, 1, n); %在[0, pi]内服从均匀分布随机产生n个数
for i=1:n
if y(i) < (l/2)*sin(theta(i))
k = k + 1;
end
end
f = k / n;
Pi = (2*l*n)/(a*k);
结果如图所示:

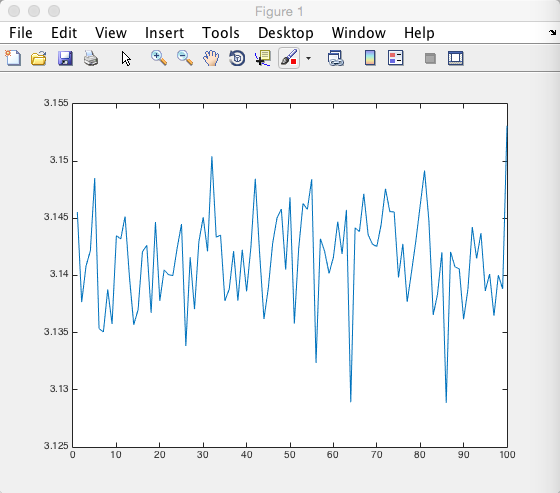
如此进行多次实验,进行估计。
如图为进行100次重复投针实验,每次投针1000000次,结果如图所示: