广度优先算法与NCurses迷宫
概述
广度优先算法也是一种图的遍历(挨个访问)算法。像在线性表中那样,在图 如果我们有这种挨个访问每个节点的能力,我们就具有了搜索的能力。这就是广度优先算法。
我在这里用ncurses字符图形库写成了一个广度优先算法的示例程序, ncurses部分的代码内容在深度优先算法里面有详细的解释。这里先粗略的感受一下广度优先算法的逻辑 广度优先算法
广度优先算法
它并不像深度优先算法那样,在一个方向上深入下去,直到某种情况(例如:碰到墙壁)发生之后, 递归上升。 它是由点及面,然后处理面上各点,各点再由点及面这样进行下去。 它借助了队列这种数据结构达成处理的目的,它是怎样借助的可以由看代码直接感受到。
我这里没有考虑没有出口的情况下,广度优先算法的行为结果。之后会有专门的研究文章。
算法过程
首先我说,我们有一个队列(对,我说有就有)。然后我们再来看一个坐标系:
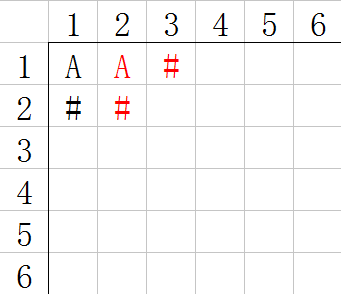
此时A位于坐标(1,1),再走一步(单位长度)它可以到达的点是(1,2)和(2,1) 图中用‘#’进行了标定。我们先把第一个点(1,1)入队,队头指针指向它
我们以 右、下、左、上这样的顺序去考虑这个问题, 让A移动到(1,2)这个位置:
此时A可以一步到达的坐标是(1,3)和(2,2),我们让这两个坐标先后分别入队
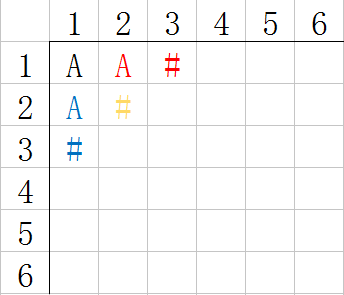
我们考虑完了 以A(1,1)点为基础点,向右一步的情况,我们再考虑以(1, 1)为基础点,向下一步的情况 如图:
此时A可以一步到达的坐标是(3,1)和(2,2), 但是(2,2)我们已经在之前的过程中考虑过了,所以我们不应该重复访问。所以之后我们写代码需要一个标记数组。来标记这个点已经处理过。在这里 我们让(3,1)这个坐标入队
显然A(1,1)不能往左边或者上边走。所以这两种情况这里就在这里不考虑了
以上就是我所谓以点及面。
那现在的情况是什么? 现在队列里面已经不仅仅是一个点的坐标了。有好几个点的坐标等待处理,而我们只需要把队头指针向后移动,挨个处理队头指针指向的点。我们就可以处理完所有的点了。
有点像是把二维的每个点推到了一个一维的情况下,然后处理一维的情况,处理面中各点
代码
因为之前我已经有过对于迷宫程序的介绍,这里, 所以现在我只对寻路这部分进行剖析。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
void go_through(WINDOW *w, Person *p)
{
// 获得当前点的坐标
int cy, cx;
cy = p->y;
cx = p->x;
// 存放下一个点的坐标
int ny, nx;
// 我们需要的数组队列
MLoc que[30 * 13] = {0};
// 找到出口与否的标记
int find = 0;
// 两个头尾指针,这里的套路跟我之前讲过的队列的套路不一致
int head, tail;
head = tail = 1;
// 把第一个点入队
que[tail].y = cy;
que[tail].x = cx;
que[tail].s = 0;
// tail指向了可以存放数据的节点,head指向了当前被处理的节点
tail++;
// book是一个全局变量,这里标记当前点已被处理
book[cy][cx] = 1;
// next数组是一个计算下一个点的坐标的工具
// next[i][j]中的i可以决定方向,而j的值决定y还是x坐标 我们这里是先行后列
int next[4][2] = {
{0, 1},
{1, 0},
{0, -1},
{-1, 0},
};
// 当队列没有被处理完成的时候
while (head < tail) {
// 分别考虑head指向点的各个方向的情况
for (int i = 0; i < 4; ++i) {
// 计算下一个点的坐标
ny = que[head].y + next[i][0];
nx = que[head].x + next[i][1];
// 如果下一个点越界,那么结束这个方向上的考虑
if (ny > 10 || ny < 0 || nx > 29 || nx < 0)
{
continue;
}
// 如果下个点不是墙,也没有走过
if (myth[ny][nx] != '*' && book[ny][nx] == 0) {
// moveTo是一个与curses有关的我自己写成的函数,它负责在图形界面上人的移动
moveTo(w, p, ny, nx);
// 微秒级的sleep
usleep(80000);
// 标定这个点被处理过
book[ny][nx] = 1;
// 把这个点推入队列内
que[tail].y = ny;
que[tail].x = nx;
// 这里是计算步数,没有使用
que[tail].s = que[head].s + 1;
// 把tail移动到下一个可写位置
tail++;
}
// 如果已经走到了出口,出口坐标是(2, 29)
if (ny ==2 && nx == 29) {
// 标记找到了迷宫出口
find = 1;
break;
}
}
// 非常重要,head指针向后移动,挨个处理由tail推入的各个点
head++;
// 如果找到了这个点
if (find) {
// ncurses的打印函数
attron(A_REVERSE);
mvwprintw(stdscr, (LINES-15)/2 + 4 + 6, (COLS-50)/2 - 20 + 60, " DONE ");
attroff(A_REVERSE);
wrefresh(stdscr);
// 跳出while循环
break;
}
}
}
|
总结
不管是深度优先算法还是广度优先算法,只要有了切身体会,代码实践。它们都是也只是非常简单有趣的算法内容。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号