2023 计算机程序设计大作业报告
github:https://github.com/litluo/ComputerProgramming-Reversi
一、项目简介
本大作业完成的是一个经典黑白棋(翻转棋)游戏,支持人机对战和人人对战。
其基本规则为:
- 棋盘为8*8的方格,初始时棋盘中央4个方格放置黑白两枚棋子,黑棋先手。
- 每一步棋,玩家可以将自己的棋子放置在棋盘上的一个空格上,使得棋盘上与该棋子同色的一条直线(横、竖、斜)的末端是玩家所下的棋子,然后将这条直线上的所有对方棋子翻转成己方棋子。
- 如果一方无子可下,则结束游戏。游戏结束时,棋盘上棋子较多的一方获胜。
二、项目实现
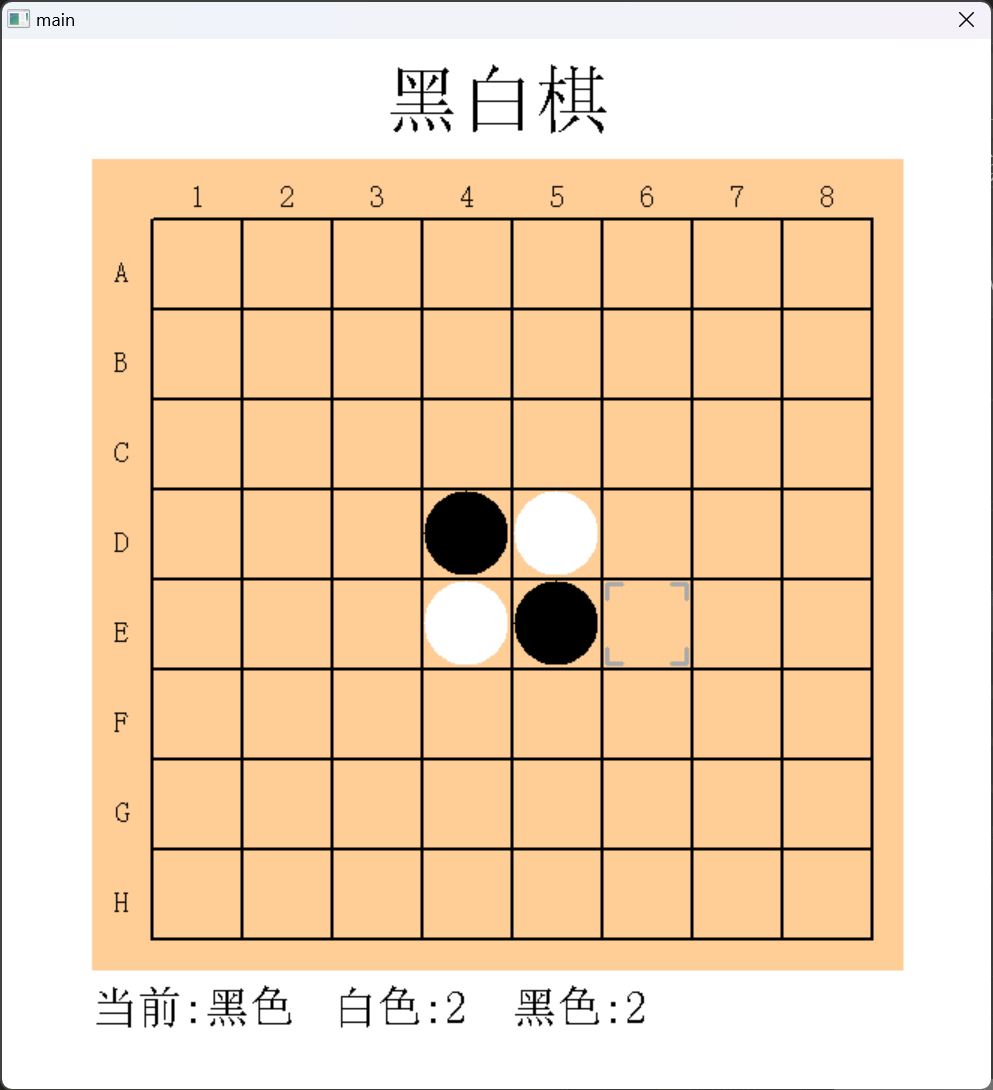
1. 游戏界面
游戏界面使用EasyX实现,主要包括棋盘、棋子、计分板等。
drawChessboard 函数用于绘制棋盘,其主要代码如下:
void drawChessboard(){
TCHAR strnum[8][3] = { _T("1"),_T("2") ,_T("3") ,_T("4"),_T("5") ,_T("6"), _T("7"), _T("8")};
TCHAR strabc[8][3] = { _T("A"),_T("B") ,_T("C") ,_T("D"),_T("E") ,_T("F"), _T("G"), _T("H")};
setbkcolor(WHITE);
cleardevice();
setbkmode(TRANSPARENT);
setfillcolor(RGB(255, 205, 150));
solidrectangle(leftLenth-20, upLenth-20, leftLenth+N*step+40, upLenth+N*step+40);
setlinestyle(PS_SOLID,2);
setcolor(RGB(0,0,0));
for(int i = 0; i <= N; i++){
line(i*step+leftLenth+20,upLenth+20,i*step+leftLenth+20,N*step+upLenth+20);
line(leftLenth+20,i*step+upLenth+20,N*step+leftLenth+20,i*step+upLenth+20);
}
settextstyle(20, 0, _T("宋体"));
for (int i = 0; i < N; i++)
{
outtextxy(leftLenth+step*i+step/2+15, upLenth-5, strnum[i]);
outtextxy(leftLenth-5, upLenth+step*i+step/2+15, strabc[i]);
}
settextstyle(50, 0, _T("宋体"));
RECT r = {0, 0, leftLenth+N*step+rightLenth+20, upLenth-20};
drawtext(_T("黑白棋"), &r, DT_CENTER | DT_VCENTER | DT_SINGLELINE);
for (int i = 0; i < N; i++){
for (int j = 0; j < N; j++){
box[i][j].x1 = leftLenth+20+i*step+3;
box[i][j].y1 = upLenth+20+j*step+3;
box[i][j].x2 = leftLenth+20+i*step+step-4;
box[i][j].y2 = upLenth+20+j*step+step-4;
}
}
}
其中,leftLenth 和 upLenth 表示棋盘左上角的坐标,step 表示棋盘格子的边长,box 数组存储每个格子的坐标。
drawScore 函数用于绘制计分板,其主要代码如下:
void drawScore(int col, BOARD selfboard, int stu = 0){
settextstyle(30, 0, _T("宋体"));
char str[20];
RECT r;
clearrectangle(leftLenth-20, upLenth+N*step+50, leftLenth+20+8*step, upLenth+N*step+90);
r = {leftLenth-20, upLenth+N*step+50, leftLenth+20+2*step, upLenth+N*step+90};
sprintf(str, "当前:%s", col ? "白色" : "黑色");
drawtext(_T(str), &r, DT_SINGLELINE);
r = {leftLenth+20+2*step, upLenth+N*step+50, leftLenth+20+4*step, upLenth+N*step+90};
sprintf(str, "黑色:%d", selfboard.cnt[0]);
drawtext(_T(str), &r, DT_SINGLELINE);
r = {leftLenth+20+4*step, upLenth+N*step+50, leftLenth+20+6*step, upLenth+N*step+90};
sprintf(str, "白色:%d", selfboard.cnt[1]);
drawtext(_T(str), &r, DT_SINGLELINE);
r = {leftLenth+20+6*step, upLenth+N*step+50, leftLenth+20+8*step, upLenth+N*step+90};
switch (stu){
case 0:
drawtext(_T(""), &r, DT_SINGLELINE);
break;
case 1:
drawtext(_T("校验中"), &r, DT_SINGLELINE);
break;
case 2:
drawtext(_T("电脑思考"), &r, DT_SINGLELINE);
break;
}
}
2. 游戏逻辑
棋盘存储采用类 Board 实现,其主要成员函数如下:
class BOARD{
public:
BOARD(){
memset(chess, -1, sizeof(chess));
cnt[0] = cnt[1] = 2;
chess[3][3] = chess[4][4] = 0;
chess[3][4] = chess[4][3] = 1;
}
public:
int chess[N][N]; // -1 for empty, 0 for black, 1 for white
int cnt[2];
public:
void draw(int x, int y);
bool check(int x, int y, int col);
int checkLine(int x, int y, int dx, int dy, int col);
void reversi(int x, int y, int col, int d);
void reversiLine(int x, int y, int dx, int dy, int tot, int col, int d);
bool checkAvilable(int col);
void copy(BOARD selboard);
void play(int x, int y, int col, int d);
};
其中 chess 数组存储棋盘上的棋子,cnt 数组存储黑白棋子的数量。
draw 函数是将棋盘上的棋子绘制出来
void BOARD::draw(int x, int y){
int rx = leftLenth+20+x*step+step/2;
int ry = upLenth+20+y*step+step/2;
COLORREF color = chess[x][y] ? WHITE : BLACK;
setfillcolor(color);
setlinecolor(color);
setlinestyle(PS_SOLID, 2);
fillcircle(rx-0.5, ry-0.5, step/2-3);
return;
}
check 函数是判断在 (x, y) 处落子是否合法
bool BOARD::check(int x, int y, int col){
int dx[8] = {0, 1, 1, 1, 0, -1, -1, -1};
int dy[8] = {1, 1, 0, -1, -1, -1, 0, 1};
for (int k = 0; k < 8; k++){
int tot = checkLine(x, y, dx[k], dy[k], col);
if (tot){
return true;
}
}
return false;
}
checkLine 函数是判断在 (x, y) 处落子后,沿着 (dx, dy) 方向是否可以翻转对方棋子
int BOARD::checkLine(int x, int y, int dx, int dy, int col){
int i, j;
for (i = x+dx, j = y+dy; i >= 0 && i < 8 && j >= 0 && j < 8; i += dx, j += dy){
if (chess[i][j] == -1) break;
if (chess[i][j] == col && i == x+dx && j == y+dy) break;
if (chess[i][j] == col && (i != x+dx || j != y+dy)){
if(dx != 0)
return (i-x)/dx - 1;
return (j-y)/dy - 1;
}
}
return 0;
}
reversi 函数是在 (x, y) 处落子后,沿着 (dx, dy) 方向翻转对方棋子
void BOARD::reversi(int x, int y, int col, int d){
int dx[8] = {0, 1, 1, 1, 0, -1, -1, -1};
int dy[8] = {1, 1, 0, -1, -1, -1, 0, 1};
for (int k = 0; k < 8; k++){
int res = checkLine(x, y, dx[k], dy[k], col);
if (res){
reversiLine(x, y, dx[k], dy[k], res, col, d);
cnt[col] += res;
cnt[!col] -= res;
}
}
cnt[col] += 1;
}
reversiLine 函数是在 (x, y) 处落子后,沿着 (dx, dy) 方向翻转对方棋子
void BOARD::reversiLine(int x, int y, int dx, int dy, int tot, int col, int d){
for (int i = x+dx, j = y+dy; tot; i += dx, j += dy, tot--){
chess[i][j] = col;
if (d)
draw(i, j);
}
}
checkAvilable 函数是判断当前玩家是否有合法的落子点
bool BOARD::checkAvilable(int col){
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
if (chess[i][j] == -1 && check(i, j, col))
return true;
return false;
}
copy 函数是将当前棋盘复制到另一个棋盘
void BOARD::copy(BOARD selfboard){
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
(*this).chess[i][j] = selfboard.chess[i][j];
(*this).cnt[0] = selfboard.cnt[0];
(*this).cnt[1] = selfboard.cnt[1];
}
play 函数是在 (x, y) 处落子后,沿着 (dx, dy) 方向翻转对方棋子,并更新棋盘。
void BOARD::play(int x, int y, int col, int d){
chess[x][y] = col;
if (d)
draw(x, y);
reversi(x, y, col, d);
if (d){
box[x][y].color = LIGHTCYAN;
box[x][y].draw();
int lx = las.first, ly = las.second;
if (lx != -1 && ly != -1){
box[lx][ly].color = RGB(255, 205, 150);
box[lx][ly].draw();
}
las = make_pair(x, y);
//printf("%d %d\n", x, y);
}
}
其中参数 d 表示是否绘制该棋盘,d = 0 表示不绘制,d = 1 表示绘制,该参数用于在计算机模拟对战时,计算机不需要绘制棋盘。
3. 人类落子
人类玩家位置鼠标标记控件设计如下:
通过一直循环,不断获取鼠标位置,当鼠标在对应格子内时,显示鼠标标记,否则隐藏鼠标标记。
该标记采用类 BOX 实现,其主要成员函数如下:
class BOX{
public:
int x1, y1, x2, y2;
int used = 0;
COLORREF color = RGB(255, 205, 150);
public:
void draw();
};
其中,x1, y1, x2, y2 表示标记的左上角和右下角坐标,used 表示标记是否被使用,color 表示标记的颜色。
下定义人类类 HumanPlayer,其主要成员函数如下:
class HumanPlayer{
public:
HumanPlayer(int col):col(col){
;
}
private:
int col;
public:
void play(BOARD *selfboard);
};
其中,col 表示玩家的颜色,play 函数用于玩家落子。
void HumanPlayer::play(BOARD *selfboard){
int oldi, oldj;
while(1){
MOUSEMSG mouse = GetMouseMsg();
for (int i = 0; i < N; i++){
for (int j = 0; j < N; j++){
if (mouse.x >= box[i][j].x1 && mouse.x <= box[i][j].x2 && mouse.y >= box[i][j].y1 && mouse.y <= box[i][j].y2){
if ((*selfboard).chess[i][j] != -1)
continue;
if (mouse.mkLButton){
if ((*selfboard).chess[i][j] == -1){
if ((*selfboard).check(i, j, col)){
box[oldi][oldj].color = RGB(255, 205, 150);
box[oldi][oldj].draw();
(*selfboard).play(i, j, col, 1);
return;
}
}
}
if (i != oldi || j != oldj){
box[i][j].color = LIGHTGRAY;
box[i][j].draw();
box[oldi][oldj].color = RGB(255, 205, 150);
box[oldi][oldj].draw();
oldi = i, oldj = j;
}
}
}
}
}
}
通过不断读取鼠标信息,当鼠标在棋盘上时,判断鼠标是否按下,如果按下,则判断该位置是否可以落子,如果可以落子,则落子并返回。
4. 计算机恒定策略落子
本人参考了 Roxanne 与 Mobility 两种策略,分别对应地定义了两个类 RoxannePlayer 和 MobilityPlayer,其主要成员函数如下:
class RoxannePlayer{
public:
RoxannePlayer(int col):col(col){
}
private:
int roxanne_table[N][N] = {
{1, 5, 3, 3, 3, 3, 5, 1},
{5, 5, 4, 4, 4, 4, 5, 5},
{3, 4, 2, 2, 2, 2, 4, 3},
{3, 4, 2, 9, 9, 2, 4, 3},
{3, 4, 2, 9, 9, 2, 4, 3},
{3, 4, 2, 2, 2, 2, 4, 3},
{5, 5, 4, 4, 4, 4, 5, 5},
{1, 5, 3, 3, 3, 3, 5, 1}
};
int col;
public:
void play(BOARD *selfboard, int d);
};
class MobilityPlayer{
public:
MobilityPlayer(int col):col(col){
}
private:
int mobility_table[N][N] = {
{1, 8, 2, 4, 4, 2, 8, 1},
{8, 9, 7, 6, 6, 7, 9, 8},
{2, 7, 3, 5, 5, 3, 7, 2},
{4, 6, 5, 10, 10, 5, 6, 4},
{4, 6, 5, 10, 10, 5, 6, 4},
{2, 7, 3, 5, 5, 3, 7, 2},
{8, 9, 7, 6, 6, 7, 9, 8},
{1, 8, 2, 4, 4, 2, 8, 1}
};
int col;
public:
void play(BOARD *selfboard, int d);
};
其中,roxanne_table 和 mobility_table 分别表示 Roxanne 与 Mobility 策略的权重表,col 表示该电脑的颜色,play 函数用于计算机落子。
void RoxannePlayer::play(BOARD *selfboard, int d){
int mminx, mminy, mmin = 8;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++){
if((*selfboard).chess[i][j] == -1 && roxanne_table[i][j] < mmin && (*selfboard).check(i, j, col))
mminx = i, mminy = j, mmin = roxanne_table[i][j];
else if ((*selfboard).chess[i][j] == -1 && roxanne_table[i][j] == mmin && rand()%2 && (*selfboard).check(i, j, col))
mminx = i, mminy = j, mmin = roxanne_table[i][j];
}
(*selfboard).play(mminx, mminy, col, d);
}
Mobility 策略与 Roxanne 策略类似,不再赘述。
值得多提的一点,是为了保证同权重的点落子的随机性,避免后面再MCTS中模拟出现单一结果,我在 if 语句中加入了 rand()%2 的判断,这样可以保证同权重的点落子的随机性。
5.MCTS法计算机落子
1. MCTS算法
MCTS算法的基本思想是,通过模拟大量的随机对局,来评估每个落子点的胜率,从而选择最优的落子点。
其主要包含四个步骤:
- select: 从根节点开始,根据一定的策略选择子节点,直到达到叶子节点。
- expand: 对叶子节点进行扩展,生成子节点。
- simulate: 对子节点进行模拟对局,直到结束。
- back_prop:根据模拟对局的结果,更新每个节点的胜率。
其定义类 MCTSPlayer,其主要成员函数如下:
class MCTSPlayer{
public:
MCTSPlayer(int col):col(col){
;
}
private:
int col;
int tick;
public:
void play(BOARD *selfboard);
private:
pii mcts(BOARD selfboard);
TreeNode* select(TreeNode *node, BOARD *selfboard);
void expand(TreeNode *node, BOARD *selfboard);
int simulate(TreeNode *node, BOARD selfboard);
void back_prop(TreeNode *node, int score);
};
其中 TreeNode 类定义如下:
class TreeNode{
public:
TreeNode(TreeNode *parent, int col):parent(parent), col(col){
for (int i = 0; i < 64; i++)
child[i] = NULL;
}
public:
TreeNode *parent;
TreeNode *child[64];
pair<int, int> pos;
int w = 0;
int n = 0;
int col = 0;
};
其中 parent 表示父节点,child 表示子节点,pos 表示落子点,w 表示胜利次数,n 表示模拟次数,col 表示落子颜色。
2. MCTS select 实现
MCTS select 实现的主要思想是,从根节点开始,根据一定的策略选择子节点,直到达到叶子节点。
TreeNode* MCTSPlayer::select(TreeNode *node, BOARD *selfboard){
if ((*node).child[0] == NULL)
return node;
TreeNode *mmove;
double mmax = -1;
int i = 0;
while((*node).child[i] != NULL){
if ((*(*node).child[i]).n == 0){
mmove = (*node).child[i];
break;
}
int N = (*node).n;
int n = (*(*node).child[i]).n;
int w = (*(*node).child[i]).w;
double score = (double)w / n + sqrt(2.0 * log(N) / n);
if (score > mmax){
mmax = score;
mmove = (*node).child[i];
}
i++;
}
if (node->parent != NULL){
int x = (*mmove).pos.first, y = (*mmove).pos.second;
(*selfboard).chess[x][y] = !(*node).col;
(*selfboard).reversi(x, y, !(*node).col, 0);
}
return select(mmove, selfboard);
}
其中权重计方法为 UCT 算法,其计算公式如下:\(\frac{w}{n} + \sqrt{\frac{2\log N}{n}}\)
3. MCTS expand 实现
MCTS expand 实现的主要思想是,对叶子节点进行扩展,生成子节点。
void MCTSPlayer::expand(TreeNode *node, BOARD *selfboard){
int tot = 0;
while((*node).child[tot] != NULL)
tot++;
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++){
if ((*selfboard).chess[i][j] == -1 && (*selfboard).check(i, j, (*node).col)){
(*node).child[tot] = new TreeNode(node, !((*node).col));
(*(*node).child[tot]).pos = make_pair(i, j);
tot++;
}
}
}
4. MCTS simulate 实现
MCTS simulate 实现的主要思想是,对子节点进行模拟对局,直到结束。
int MCTSPlayer::simulate(TreeNode *node, BOARD selfboard){
int colnow = (*node).col;
BOARD silentboard;
silentboard.copy(selfboard);
while(true){
if (!silentboard.checkAvilable(colnow)){
break;
}
RoxannePlayer roxanneplayer = RoxannePlayer(colnow);
roxanneplayer.play(&silentboard, 0);
colnow = !colnow;
}
return silentboard.cnt[col] > silentboard.cnt[!col] ? 1 : 0;
}
5. MCTS back_prop 实现
MCTS back_prop 实现的主要思想是,根据模拟对局的结果,更新每个节点的胜率。
void MCTSPlayer::back_prop(TreeNode *node, int score){
(*node).n++;
(*node).w += score;
if ((*node).parent != NULL)
back_prop((*node).parent, score);
}
6. MCTS mcts 本体实现
MCTS mcts 本体实现的主要思想是,通过模拟大量的随机对局,来评估每个落子点的胜率,从而选择最优的落子点。
pii MCTSPlayer::mcts(BOARD selfboard){
TreeNode root = TreeNode(NULL, col);
while (time(NULL) - tick < 3){
BOARD silentboard;
silentboard.copy(selfboard);
TreeNode *choice;
choice = select(&root, &silentboard);
expand(choice, &silentboard);
int score = simulate(choice, silentboard);
/*
if ((*choice).col != col)
score = 1 - score;
*/
back_prop(choice, score);
}
int mmax = -1;
TreeNode *mmove;
int i = 0;
while(root.child[i] != NULL){
//printf("%d %d %d %d\n", (*root.child[i]).pos.first, (*root.child[i]).pos.second, (*root.child[i]).w, (*root.child[i]).n);
if ((*root.child[i]).n > mmax){
mmax = (*root.child[i]).n;
mmove = root.child[i];
}
i++;
}
return (*mmove).pos;
}
其中,root 表示根节点,choice 表示选择的节点,mmove 表示最优的落子点。
tick 表示开始计时的时间,time(NULL) 表示当前时间,当当前时间减去开始计时的时间大于3秒时,结束模拟。
返回值为最优的落子点。
6.游戏本体
1. 游戏模式选择
定义 init 函数,通过命令行参数选择游戏模式,其主要代码如下:
void init(int *player){
printf("请选择玩家:\n");
printf("1.人类玩家\n");
printf("2.电脑1(Roxanne策略)\n");
printf("3.电脑2(Mobility策略)\n");
printf("4.电脑3(MCTS策略)\n");
while(player[0] < 1 || player[0] > 4){
printf("请输入玩家1(黑棋先手):");
scanf("%d", &player[0]);
}
while(player[1] < 1 || player[1] > 4){
printf("请输入玩家2(白棋后手):");
scanf("%d", &player[1]);
}
initgraph(leftLenth+N*step+rightLenth+20, upLenth+N*step+downLenth+20, NOMINIMIZE);
return;
}
2. 游戏运行
定义 game 函数,实现游戏本体,其主要代码如下:
void game(int player[2]){
bool col = 0;
las = make_pair(-1, -1);
BOARD showboard;
showboard.draw(3, 3);
showboard.draw(4, 4);
showboard.draw(3, 4);
showboard.draw(4, 3);
drawScore(col, showboard);
while(true){
switch(player[col]){
case 1:{
HumanPlayer humanplayer = HumanPlayer(col);
humanplayer.play(&showboard);
break;
}
case 2:{
drawScore(col, showboard, 2);
RoxannePlayer roxanneplayer = RoxannePlayer(col);
Sleep(1000);
roxanneplayer.play(&showboard, 1);
break;
}
case 3:{
drawScore(col, showboard, 2);
MobilityPlayer mobilityplayer = MobilityPlayer(col);
Sleep(1000);
mobilityplayer.play(&showboard, 1);
break;
}
case 4:{
drawScore(col, showboard, 2);
MCTSPlayer mctsplayer = MCTSPlayer(col);
mctsplayer.play(&showboard);
break;
}
}
col = !col;
drawScore(col, showboard, 1);
if (!showboard.checkAvilable(col)){
break;
}
drawScore(col, showboard, 0);
}
drawWin(showboard);
printf("%s胜\n", showboard.cnt[0] > showboard.cnt[1] ? "黑色" : "白色");
while(true){
MOUSEMSG mouse = GetMouseMsg();
if (mouse.mkLButton)
break;
}
return;
}
其中,col 表示当前玩家的颜色,showboard 表示需要绘制棋盘。
其中 las 表示上一次落子的位置,用于在绘制棋盘时,将上一次落子的位置的标记恢复为原来的颜色。
drawWin 函数用于绘制游戏结束时的界面,其主要代码如下:
void drawWin(BOARD selfboard){
settextstyle(60, 0, _T("宋体"));
settextcolor(RED);
clearrectangle(leftLenth-20, upLenth+N*step+50, leftLenth+20+8*step, upLenth+N*step+90);
RECT r = {leftLenth-20, upLenth+N*step+50, leftLenth+20+8*step, upLenth+N*step+downLenth+10};
if (selfboard.cnt[0] > selfboard.cnt[1]){
drawtext(_T("黑色胜"), &r, DT_CENTER | DT_VCENTER | DT_SINGLELINE);
}
else if (selfboard.cnt[0] < selfboard.cnt[1]){
drawtext(_T("白色胜"), &r, DT_CENTER | DT_VCENTER | DT_SINGLELINE);
}
else{
drawtext(_T("平局"), &r, DT_CENTER | DT_VCENTER | DT_SINGLELINE);
}
}
三、总结
本次大作业中,我避免了使用大量的全局变量,将棋盘等信息封装成类,再使用所学的指针知识,将类的对象作为参数传递,使得代码更加规范,避免了多个棋盘同时出现的混乱情况。
虽然在实现程序功能的过程中,我遇到了很多问题,但是通过查阅资料,我都一一解决了,这也让我对C和C++的使用更加熟练。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号