排序算法:merge sort(python)
基本原理
merge sort就是用divide and conquer的方法来实现sort。
它将一个要倍排序的序列,分成两个已经排好序的序列,在将他们的合并起来。

在合并的时候,首先指针都在两个序列的最前端,然后比较大小,将符合的放入新的序列中,指针再后移,再进行相同的比较过程。
错误的第一次实现
错误示例!
#merge sort
def merge(L_l,L_r):
i = 0
j = 0
L_new = []
while i<len(L_l) and j<len(L_r):
if L_l[i] > L_r[j]:
L_new.append(L_l[i])
i += 1
elif L_l[i] < L_r[j]:
L_new.append(L_r[j])
j += 1
else:
L_new.append(L_r[j])
L_new.append(L_l[i])
i += 1
j += 1
print("L_new="+str(L_new))
return L_new
def mergesort(L):
print("lenl="+str(len(L)))
if len(L) <= 1:
return L
else:
mid = len(L)//2
print("mid="+str(mid))
L_sort = L[:]
lefthalf = L[:mid]
righthalf = L[mid:]
L_l = mergesort(lefthalf)
print("L_l done")
print("L_l="+str(L_l))
# mid = len(L)//2
print("mid2="+str(mid))
# L_sort = L[:]
L_r = mergesort(righthalf)
L = merge(L_l,L_r)
return L
L = [1,5,6,3,7,8]
mergesort(L)
print(L)
此方法错误,打印debug信息如下。
L(1)=[1, 5, 6, 3, 7, 8]
mid(1)=3
lefthalf(1)=[1, 5, 6]
righthalf(1)=[3, 7, 8]
L(2)=[1, 5, 6]
mid(2)=1
lefthalf(2)=[1]
righthalf(2)=[5, 6]
L(3)=[1]
L_l_after(2=[1]
L(3)=[5, 6]
mid(3)=1
lefthalf(3)=[5]
righthalf(3)=[6]
L(4)=[5]
L_l_after(3=[5]
L(4)=[6]
L_r_after(3=[6]
L_new=[6]
L_after(3=[6]
L_r_after(2=[6]
L_new=[6]
L_after(2=[6]
L_l_after(1=[6]
L(2)=[3, 7, 8]
mid(2)=1
lefthalf(2)=[3]
righthalf(2)=[7, 8]
L(3)=[3]
L_l_after(2=[3]
L(3)=[7, 8]
mid(3)=1
lefthalf(3)=[7]
righthalf(3)=[8]
L(4)=[7]
L_l_after(3=[7]
L(4)=[8]
L_r_after(3=[8]
L_new=[8]
L_after(3=[8]
L_r_after(2=[8]
L_new=[8]
L_after(2=[8]
L_r_after(1=[8]
L_new=[8]
L_after(1=[8]
[1, 5, 6, 3, 7, 8]
从这个里面可以看到,是merge出的问题,没有将两个全部加入。可以发现,是while循环没有做完出现的问题。因为前面的while结束后,可能还有剩余的部分没有加入,因此需要在写循环把之后的全部加入。
更改后的代码如下:
#merge sort
def merge(L_l,L_r):
i = 0
j = 0
L_new = []
while i<len(L_l) and j<len(L_r):
if L_l[i] > L_r[j]:
L_new.append(L_l[i])
i += 1
elif L_l[i] < L_r[j]:
L_new.append(L_r[j])
j += 1
else:
L_new.append(L_r[j])
L_new.append(L_l[i])
i += 1
j += 1
while i < len(L_l):
L_new.append(L_l[i])
i += 1
while j < len(L_r):
L_new.append(L_r[j])
j += 1
# print("L_new="+str(L_new))
return L_new
def mergesort(L,count):
count += 1
# print("L("+str(count)+")="+str(L))
if len(L) <= 1:
return L
else:
mid = len(L)//2
# print("mid("+str(count)+")="+str(mid))
# L_sort = L[:]
lefthalf = L[:mid]
righthalf = L[mid:]
# print("lefthalf("+str(count)+")="+str(lefthalf))
# print("righthalf("+str(count)+")="+str(righthalf))
L_l = mergesort(lefthalf,count)
# print("L_l_after("+str(count)+"="+str(L_l))
L_r = mergesort(righthalf,count)
# print("L_r_after("+str(count)+"="+str(L_r))
L = merge(L_l,L_r)
# print("L_after("+str(count)+"="+str(L))
return L
count = 0
L = [1,5,6,3,7,8]
L_new = mergesort(L,count)
print(L_new)
此刻可以返回正确的结果。
insert sort 与 merge sort的对比
insert sort比merge sort 的优点在与内存。如果想要完成merge sort,那么需要一个theta(n)的auxiliary space(辅助空间),但是in place sort 只需要theta(1)的auxiliary space。因为merge sort需要复制左右两个序列然后把新的序列存入。
为了解决这个问题,人们提出了in-place merge sort,但是running time会很差,为theta(n^2),因此并不是常用。
时间复杂度
为nlog(n),该过程可以用树来直观的看出。
由merge sort的原理列出式子为:
T(n) = 2T(n/2) + c*n
我们可以通过一个recurrence tree来直观的看出其复杂度。

在这里树里面,每级的叶子都有相同的量。
下面一次为延伸,来使用树计算一些其他的式子的时间复杂度。
例1: T(n) = 2T(n/2) + c

在这种情况下,叶子是主导作用,因此时间复杂度以此计算。
例2: T(n) = 2T(n/2) + c*n^2
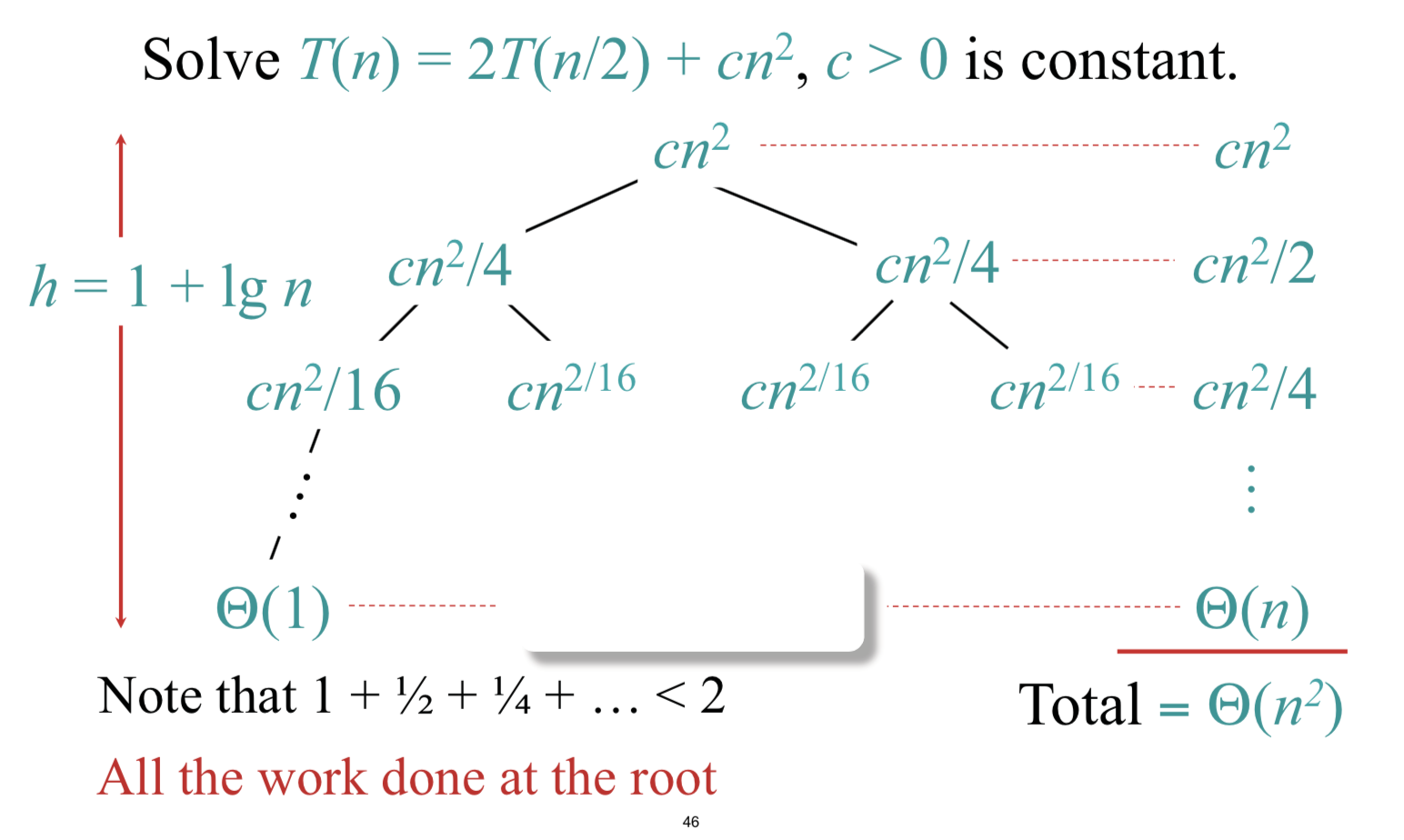
在这种情况下,根起主导作用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号