聚类
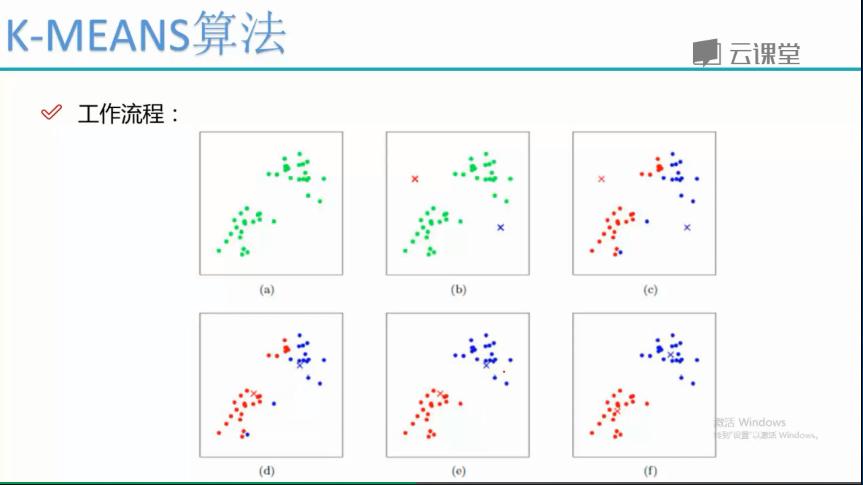
kmeans是一种无监督的聚类问题,在使用前一般要进行数据标准化, 一般都是使用欧式距离来进行区分,主要是通过迭代质心的位置
来进行分类,直到数据点不发生类别变化就停止,
一次分类别,一次变换质心,就这样不断的迭代下去
优势:使用方便
劣势:1.K值难确定
2. 复杂度与样本数量呈线性关系
3.很难发现形状任意的簇
4.容易受初始点的影响
python中使用 sklearn.cluster 模块,使用的时候需要指定参数
第一步:导入数据,提取数据中的变量保存为X
import pandas as pd beer = pd.read_csv('data.txt', sep=' ')X = beer[["calories","sodium","alcohol","cost"]]
第二步:进行kmans聚类分析
from sklearn.cluster import KMeanskm = KMeans(n_clusters=3).fit(X) #聚成三蔟
km2 = KMeans(n_clusters=2).fit(X) #聚成两蔟
beer['cluster'] = km.labels_ #返回聚类的标签结果
beer['cluster2'] = km2.labels_beer.sort_values('cluster') #根据'cluster'进行排序
第三步:根据分类结果画出带颜色的散点图,及其混淆矩阵
from pandas.tools.plotting import scatter_matrixcluster_center = km.cluster_centers_
cluster_center_2 = km2.cluster_centers_
# print(beer.groupby('cluster').mean()) #groupby进行快速分组,mean求平均
print(beer.groupby('cluster2').mean())
centers = beer.groupby("cluster").mean().reset_index() #reset_index()重新添加了序号import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 14 #rcParams 用于修改字体的大小import numpy as np
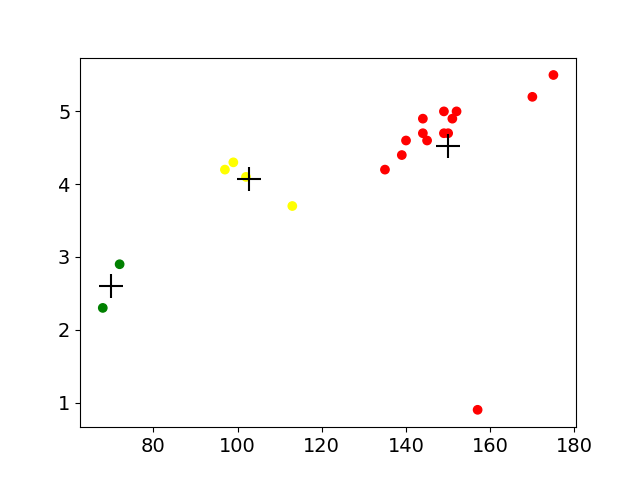
color = np.array(['red', 'green', 'yellow', 'blue'])plt.scatter(beer['calories'], beer['alcohol'], c=color[beer['cluster']])
plt.scatter(centers.calories, centers.alcohol, linewidths=3, marker='+', s=300, c='black')
scatter_matrix(beer[["calories","sodium","alcohol","cost"]], s=100,alpha = 1 ,c=color[beer['cluster']],
figsize=(10, 10)) #alpha 代表不透明的意思
plt.suptitle("With 3 centroids initialized")plt.show()

第四步:对数据进行标准化,再进行kmeans聚类
from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_scaler = scaler.fit_transform(X) #进行转换 new_X_scaler = pd.DataFrame(X_scaler, columns=["calories","sodium","alcohol","cost"])km = KMeans(n_clusters=3).fit(X_scaler)
beer['scaler_cluster'] = km.labels_
beer.sort_values('scaler_cluster')
print(beer.groupby('scaler_cluster').mean())
scatter_matrix(new_X_scaler, alpha = 1 ,c=color[beer.scaler_cluster])
plt.show()
第五步:为了比较处理前后的效果,我们引入了轮廓系数 metrics.silhouette_score,发现未标准化的分类结果要好于标准化
from sklearn import metrics score_scaled = metrics.silhouette_score(X,beer.scaler_cluster) score = metrics.silhouette_score(X,beer.cluster) print(score_scaled, score)
第六步: 我们使用轮廓系数(b(i)-a(i))/max(b(i), a(i)), b(i)一个点到自己蔟的距离,a(i)表示一个点到其他蔟的距离,来挑选蔟的参数n_clusters
scores = [] for i in range(2, 15):</span><span style="color: #0000ff;">print</span>(metrics.silhouette_score(X,KMeans(n_clusters=<span style="color: #000000;">i).fit(X).labels_)) #X变量,</span>KMeans(n_clusters=i).fit(X).labels_分类得到的标签</pre>scores.append(metrics.silhouette_score(X,KMeans(n_clusters=i).fit(X).labels_)) plt.plot(list(range(2, 15)), scores) plt.xlabel('迭代次数') plt.ylabel('轮廓系数') plt.show()





