数字图像处理
1. 图像的基本概念
- 连续图像:二维坐标系上连续变化的图像,图像的像点无限稠密。
- 离散图像:用数字序列表示的图像,像素是组成图像的基本单位。
1.1 图像数字化采样
图像经过采样与量化可以得到一幅数字图像,可以用矩阵表示。每一个像素有三个参数:x值,y值,灰度值。量化方法有等间隔量化与非等间隔量化,一般采用等间隔量化。
图像类型:二值图像、灰度图像、RGB彩色图像、索引图像。
- 二值图像,纯黑白图像,由0和1构成。可以使用以下代码将数值数组转化为逻辑数组。
B=logical(A)
- 灰度图像:整数取值范围
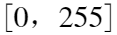 ,0表示纯黑,255表示纯白。
,0表示纯黑,255表示纯白。 - RGB彩色图像:
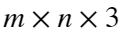 的数组,每一个像素点对应红、绿、蓝三个分量。
的数组,每一个像素点对应红、绿、蓝三个分量。 - 索引图像:有两个分量——数据矩阵X和彩色映射矩阵
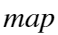 。
。
2. 亮度变换与空间滤波
空域处理表达式如下:
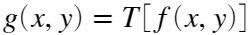
其中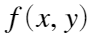 为输入图像,
为输入图像,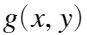 为输出图像。T为对图像进行处理的操作符。matlab可以用imadjust函数进行处理。
为输出图像。T为对图像进行处理的操作符。matlab可以用imadjust函数进行处理。
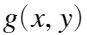 为输出图像。T为对图像进行处理的操作符。matlab可以用imadjust函数进行处理。
为输出图像。T为对图像进行处理的操作符。matlab可以用imadjust函数进行处理。g=imadjust(f,[low_in;high_in],[low_out;high_out],gamma)
此函数将图像f中的亮度值映射到g,gamma为调节权重。
图像翻转:
f=imread('pic1.jpg'); %随便准备一张图片就行
g=imadjust(f,[0;1],[1;0]);
figure(1);
subplot(1,2,1),imshow(f)
subplot(1,2,2),imshow(g)
2.1 线性空间滤波器
使用拉普拉斯滤波器增强图像的基本公式为:
式中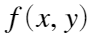 为输入的退化图像;
为输入的退化图像;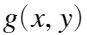 为输出的增强图像;c取1或-1.
为输出的增强图像;c取1或-1.
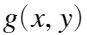 为输出的增强图像;c取1或-1.
为输出的增强图像;c取1或-1. 拉普拉斯算子定义为:
对于离散的数字图像,二阶导数用如下公式近似:
因而有:
拉普拉斯算子对图像的作用就相当于如下矩阵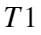 与f相乘:
与f相乘:
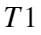 与f相乘:
与f相乘: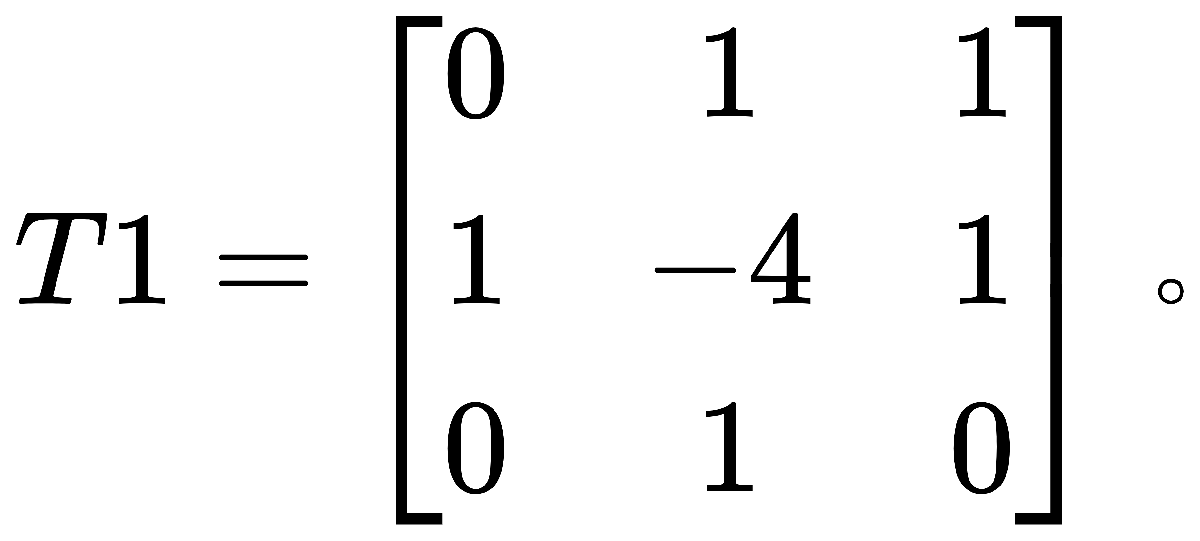
也可以用如下矩阵近似拉普拉斯算子:
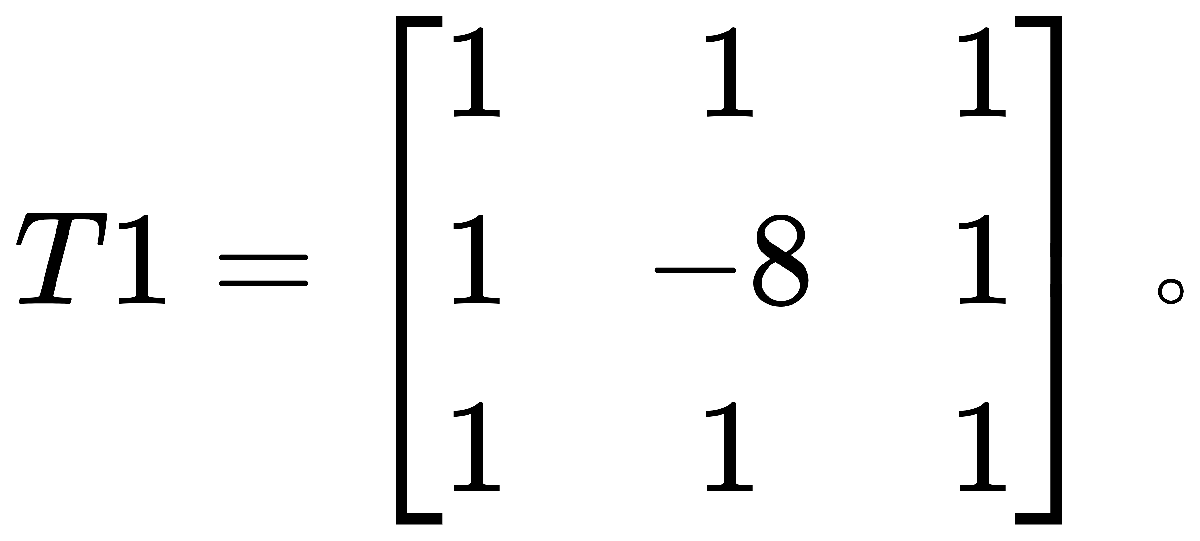
Matlab中函数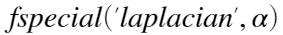 用于实现另一个更为常见的拉普拉斯算子掩模
用于实现另一个更为常见的拉普拉斯算子掩模
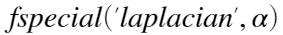 用于实现另一个更为常见的拉普拉斯算子掩模
用于实现另一个更为常见的拉普拉斯算子掩模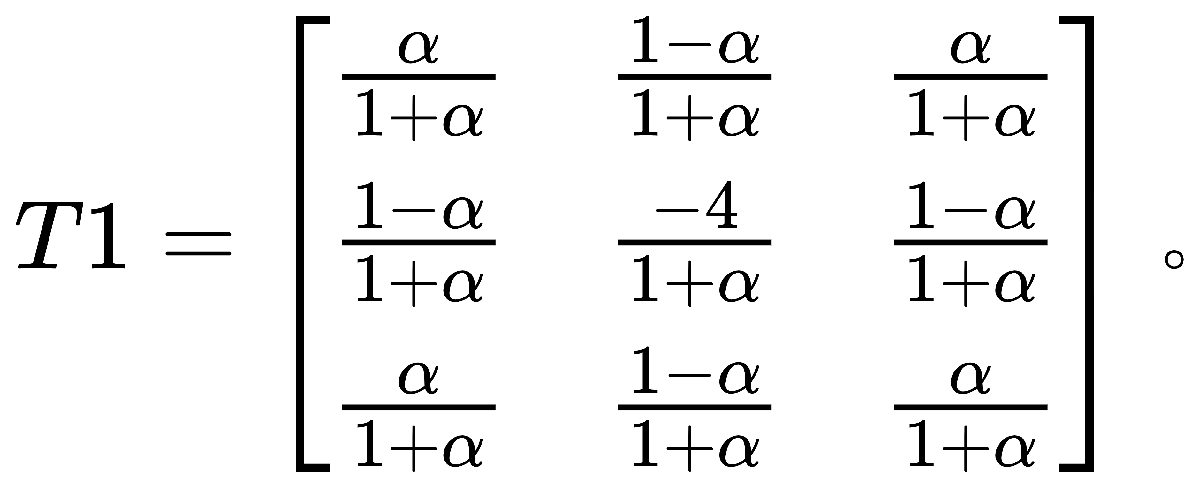
图像恢复实例:
f=imread('pic2.jpg');
h1=fspecial('laplacian',0); %采用第一个T1滤波器。
g1=f-imfilter(f,h1); %中心-4,c=-1,即从原图像减去拉普拉斯计算的结果。
h2=[1 1 1;1 -8 1;1 1 1]; %第二个T1滤波器。
g2=f-imfilter(f,h2);
figure(2);
subplot(1,3,1),imshow(f);
subplot(1,3,2),imshow(g1);
subplot(1,3,3),imshow(g2);
2.2 非线性空间滤波器
Matlab的非线性空间滤波的工具是函数ordfilt2,其响应是基于对图像领域中所包含的所有像素进行排序,然后使用排序确定的结果的值来代替邻域中所包含的中心像素的值。其语法如下:
g=ordfilt(f,order,domain)
详见官方文档。
中值滤波:
f=imread('lena.bmp'); %读原图像
f1=imnoise(f,'salt & pepper',0.02); %加椒盐噪声
g=medfilt2(f1); %进行中值滤波
figure(3);
subplot(1,3,1),imshow(f),title('原图像')
subplot(1,3,2),imshow(f1),title('被椒盐噪声污染的图像')
subplot(1,3,3),imshow(g),title('中值滤波图像')
3. 频率变换
3.1 傅里叶变换
二维连续傅里叶变换:
如果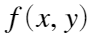 是一幅图像,那么
是一幅图像,那么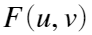 是他的谱。
是他的谱。
定义二维傅里叶变换的频谱、相位谱、和功率谱(频谱密度)如下:
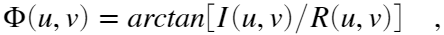
式中R与I分别为F的实部和虚部。
二维傅里叶逆变换定义为;
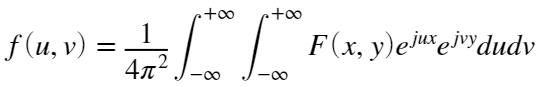
在matlab中由于对象是离散的,二维傅里叶变换的定义为:
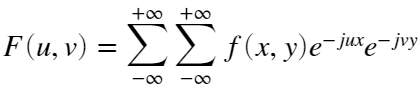
逆变换的定义为:
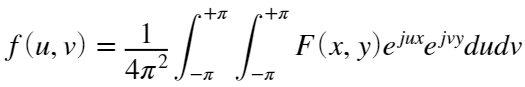
也记为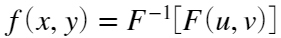 。
。
二维离散傅里叶变换(DFT)
定义如下:
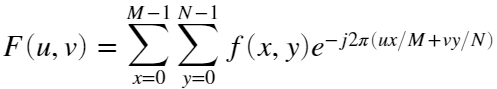
逆变换的定义为:
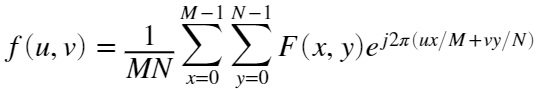
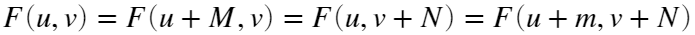
即DFT在u和v方向上都是周期的,周期性也是DFT逆变换的一个重要属性。即对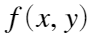 也成立。
也成立。
基于离散傅里叶变换的频率滤波
- 首先计算输入图像的傅里叶变换
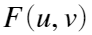 。
。 - 再用滤波器
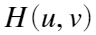 对
对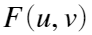 做变换。
做变换。 - 最后对其得到的变换做傅里叶的逆变换就得到频率滤波后的图像。
主要包括以下五个步骤:
- 用
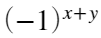 乘以图像进行中心变换,得:
乘以图像进行中心变换,得: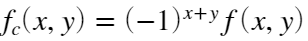
- 计算傅里叶变换:
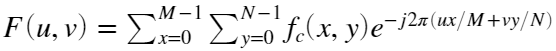
- 用滤波器
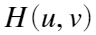 作用
作用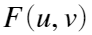 :
: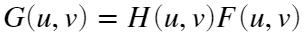
- 傅里叶逆变换并取实部:
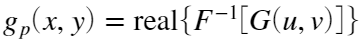
- 用
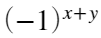 乘以
乘以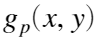 得到中心还原滤波图像:
得到中心还原滤波图像: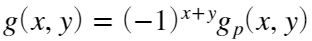
滤波传递函数:
- 理想低通道滤波器,
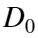 为指定的非负数,
为指定的非负数,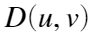 为点到(u,v)到滤波器中心的距离。
为点到(u,v)到滤波器中心的距离。
- n阶巴特沃兹低通滤波器(在距离原点
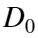 处出现的截止频率)的传递函数为:
处出现的截止频率)的传递函数为:
- 高斯低通道滤波器的传递函数:
一阶巴特沃兹低通道滤波器:
clc,clear
cm=imread('cameraman.tif'); %内置图像文件
[n,m]=size(cm); %计算图像的维数
cf=fft2(cm); %傅里叶变换
cf=fftshift(cf); %进行中心变换
u=[-floor(m/2):floor((m-1)/2)] %水平频率
v=[-floor(n/2):floor((n-1)/2)] %垂直频率
[uu,vv]=meshgrid(u,v); %频率平面上的网格节点
b1=1./(1+(sqrt(uu.^2+vv.^2)/15).^2); %构造一阶巴特沃兹滤波器
cf1=b1.*cf; %逐点相乘,进行低通滤波
cm1=real(ifft2(cf1)); %傅里叶逆变换并取实部
% cm1=ifftshift(cm1);
cm1=uint8(cm1);
figure(4);
subplot(1,2,1),imshow(cm) %显示原图像
subplot(1,2,2),imshow(cm1) %显示滤波后的图像
3.2 离散余弦变换(DCT)
二维DCT变换定义为:
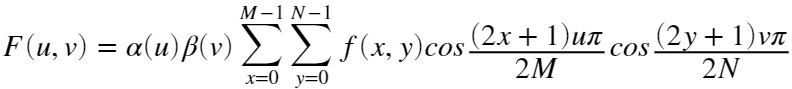
逆变换为:
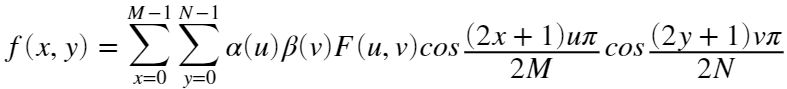
上式: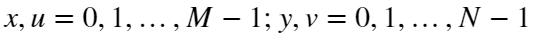 ;且
;且
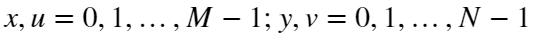 ;且
;且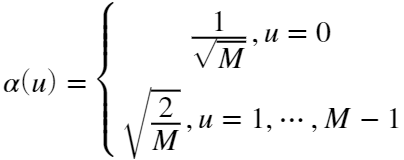
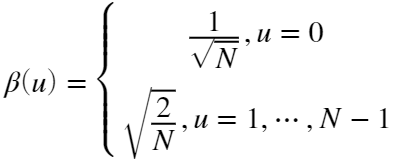
令变换核函数:
DCT变换公式可以写为:
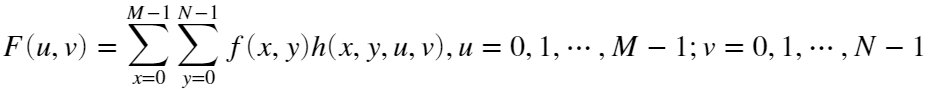
逆变换公式为:
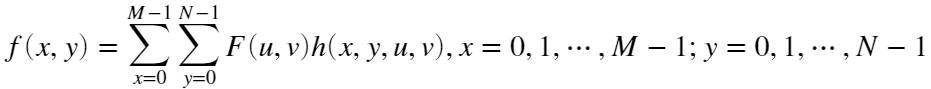
部分定义与DFT相似, 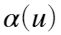 和
和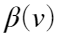 即为每一个对应的空间频率成分在原图像中所占的比重。
即为每一个对应的空间频率成分在原图像中所占的比重。
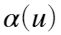 和
和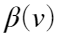 即为每一个对应的空间频率成分在原图像中所占的比重。
即为每一个对应的空间频率成分在原图像中所占的比重。 DCT变换有两种方法:基于快速傅里叶变换(FFT)的算法,基于DCT变换矩阵(Transform Matrix)的算法.
用图像的方法显示 DCT基函数矩阵:
DCT基函数矩阵:
 DCT基函数矩阵:
DCT基函数矩阵:clc, clear, T=dctmtx(8); %8×8的DCT变换矩阵
figure(5);
colormap('gray'); %设置颜色映射矩阵
for m = 1:8
for n = 1:8
subplot(8,8,(m-1)*8+n);
Y=zeros(8); Y(m,n)=1; %8×8矩阵中只有一个元素为1,其余元素都为0
X = T'*Y*T; %做逆DCT变换
imagesc(X); %显示图像
axis square %画图区域是方形
axis off %不显示轴线和标号
end
end
灰度图像压缩对比图:
I = imread('cameraman.tif'); %cameraman.tif是Matlab自带的图像文件
I = im2double(I); %数据转换成double类型
T = dctmtx(8); %T为8×8的DCT变换矩阵
figure(6);
%定义正DCT变换的匿名函数,这里block_struct是Matlab内置的结构变量
dct = @(block_struct) T * block_struct.data * T';
B = blockproc(I,[8 8],dct); %做正DCT变换
mask = [1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0]; %给出掩膜矩阵
%提取低频系数
B2 = blockproc(B,[8 8],@(block_struct) mask .* block_struct.data);
%定义逆DCT变换的隐函数
invdct = @(block_struct) T' * block_struct.data * T;
I2 = blockproc(B2,[8 8],invdct); %做逆DCT变换
subplot(1,2,1), imshow(I) %显示原图像
subplot(1,2,2), imshow(I2) %显示变换后的图像
用DCT变换对RGB彩色图像进行压缩
clc,clear
f0=imread('pic1.jpg');
f1=double(f0);
for k=1:3
g(:,:,k)=dct2(f1(:,:,k));
end
g(abs(g)<0.1)=0; %把DTC系数小于1的变为0
for k=1:3
f2(:,:,k)=idct2(g(:,:,k)); %做DTC逆变换
end
f2=uint8(f2); %将数据转换为uint8的格式
imwrite(f2,'pic2.bmp')
figure(7);
subplot(1,2,1),imshow(f0)
subplot(1,2,2),imshow(f2)
对于通常的图像来说,大多少的DCT系数的值接近0,所以重构图像画质一般不会显著下降。
3.3 图像保真度与质量
1. 客观保真度准则
输入图与输出图的均方根误差,令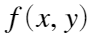 代表输入图,
代表输入图,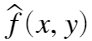 代表先压缩后解压得到的f(x,y)的近似。定义它们之间的误差如下:
代表先压缩后解压得到的f(x,y)的近似。定义它们之间的误差如下:
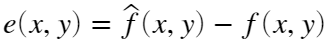
如果两幅图尺寸为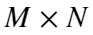 则总误差为:
则总误差为:
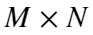 则总误差为:
则总误差为: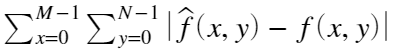 ,
, 均方根误差为:
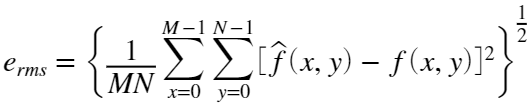
均方信噪比(Signal-to-Noise Ratio,SNR),如果将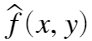 看作原始图
看作原始图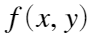 与噪声信号
与噪声信号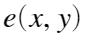 的和,那么输出的均方信噪比为:
的和,那么输出的均方信噪比为:
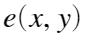 的和,那么输出的均方信噪比为:
的和,那么输出的均方信噪比为: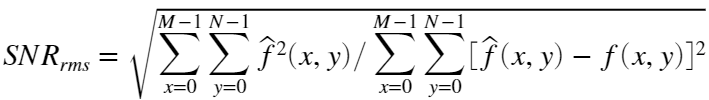
均方根误差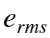 越小,峰值信噪比PSNR越大,处理图像的质量越好。
越小,峰值信噪比PSNR越大,处理图像的质量越好。
2. 主观保真度准则
以人的主观判断为主。
4. 数字水印防伪
略……
5. 图像加密与隐藏
5.1 加密算法
clc, clear
a=imread('pic1.jpg'); ws1=size(a); %读入保密图像,并计算维数
b=imread('pic2.jpg'); ws2=size(b); %读入载体图像,并计算维数
nb=imresize(b,ws1(1:2)); %把载体图像变换成与保密图像同样大小
key=-0.400001; %给出密钥,即混沌序列的初始值
L=max(ws1); x(1)=key; y(1)=key; alpha=1.4; beta=0.3;
for i=1:L-1 %生成两个混沌序列
x(i+1)=1-alpha*x(i)^2+y(i); y(i+1)=beta*x(i);
end
x(ws1(1)+1:end)=[]; %删除x后面一部分元素
[sx,ind1]=sort(x); [sy,ind2]=sort(y); %对混沌序列按照从小到大排序
ea(ind1,ind2,:)=a; %打乱保密图像的行序和列序,生成加密图像矩阵ea
figure(8);
imshow(ea) %显示保密图像加密后得到的图像
nb2=bitand(nb,240); %载体图像与11110000((二进制)=240(十进制))逐位与运算
ea2=bitand(ea,240); %加密图像与11110000逐位与运算
ea2=ea2/16; %加密图像高4位移到低4位
da=bitor(nb2,ea2); %把加密图像嵌入载体图像的低4位,构造合成图像
da2=bitand(da,15)*16; %这里15(十进制)=00001111,提取加密图像的高4位,
da3=da2(ind1,ind2,:); %对加密图像进行解密
figure(9);
subplot(1,2,1), imshow(da3) %显示提取的并解密以后的原图像
subplot(1,2,2), imshow(da) %显示嵌入加密图像的合成图像
Danke!
本文来自博客园,作者:litecdows,作者在其他博客平台均使用此昵称!
转载请注明原文链接:https://www.cnblogs.com/litecdows/p/digital_image_processing.html











 浙公网安备 33010602011771号
浙公网安备 33010602011771号