基于灰色模型和Bootstrap理论的大规模定制质量控制方法研究
基于GM的生产质量预测:
- 原始质量指标数列为:
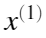 是
是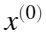 的累加序列为:
的累加序列为:
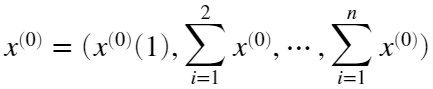
经过该处理,可以使粗糙的原始离散数列变为光滑的离散数列。
- 建立基本的预测模型GM(1,1),其白化方程为
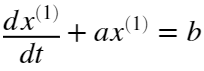
式中,a、b为常系数,且符合
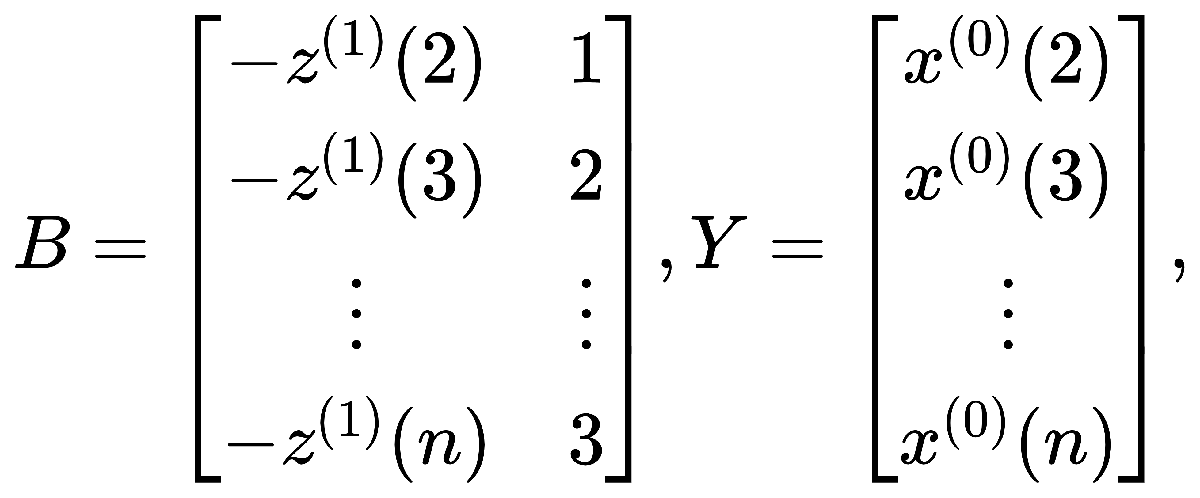
式中: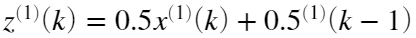 。且
。且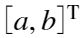 的结果是多元线性回归分析的结论得出,即满足
的结果是多元线性回归分析的结论得出,即满足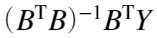 可实现最小二乘。
可实现最小二乘。
- 对建立的GM(1,1)模型进行精度检验和评估。检验依据后验差比值c和小误差概率p两个指标,模型精度等级见表。其中c与p的定义如下:
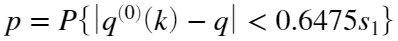 ,
,式中: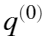 为残差序列,q为残差序列的均值;
为残差序列,q为残差序列的均值;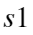 为原始序列的标准差;
为原始序列的标准差;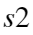 为残差序列的标准差。
为残差序列的标准差。
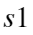 为原始序列的标准差;
为原始序列的标准差;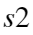 为残差序列的标准差。
为残差序列的标准差。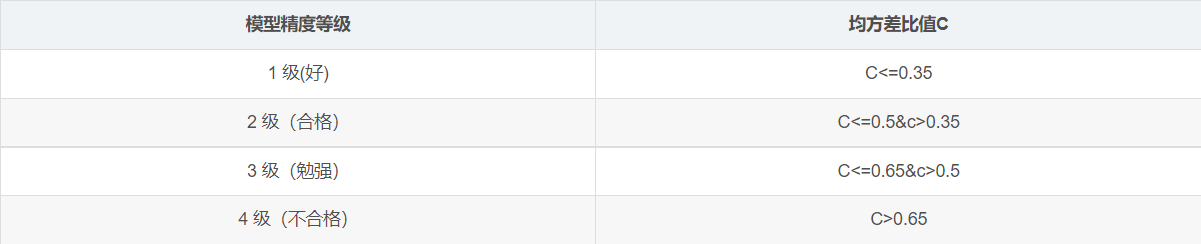
如果精度不合要求,可以用残差序列建立GM(1,1)模型对原模型进行修正,以提高其精度。若GM(1,1)满足要求时,其还原数据与预测值如下:
如果要进一步提高精度,可以采用GM(1,1)新陈代谢模型。
基于Bootstrap理论的过程质量分析:
估计误差:
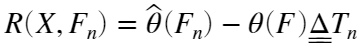
Bootstrap的实质就是再抽样的过程。
- 根据观测样本
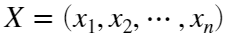 构造经验分布函数
构造经验分布函数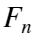 。
。 - 从
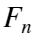 中抽取样本
中抽取样本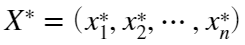 ,称其为Bootstrap样本。
,称其为Bootstrap样本。 - 计算相应的Bootstrap统计量
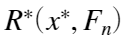 ,其表达式为:
,其表达式为:
- 重复(2)(3)B次,得到Bootstrap统计量
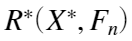 的B个可能值,将它们从小到大排列即为样本统计量的Bootstrap经验分布。
的B个可能值,将它们从小到大排列即为样本统计量的Bootstrap经验分布。 - 用
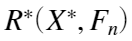 的分布去逼近
的分布去逼近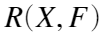 的分布,即用
的分布,即用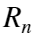 的分布去近似逼近
的分布去近似逼近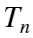 的分布,可得到参数
的分布,可得到参数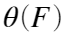 的B个统计值,即可统计求出参数θ的分布及其特征。
的B个统计值,即可统计求出参数θ的分布及其特征。
本文来自博客园,作者:litecdows,作者在其他博客平台均使用此昵称!
转载请注明原文链接:https://www.cnblogs.com/litecdows/p/GM_Bootstrap.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号