[SDOI2013]费用流

Description:

Alice和Bob在图论课程上学习了最大流和最小费用最大流的相关知识。 最大流问题：给定一张有向图表示运输网络，一个源点S和一个汇点T，每条边都有最大流量。

一个合法的网络流方案必须满足：

(1)每条边的实际流量都不超过其最大流量且非负；

(2)除了源点S和汇点T之外，对于其余所有点，都满足该点总流入流量等于该点总流出流量；而S点的净流出流量等于T点的净流入流量，这个值也即该网络流方案的总运输量。

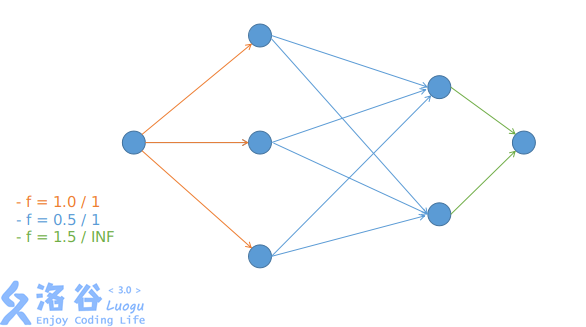
最大流问题就是对于给定的运输网络，求总运输量最大的网络流方案。 上图表示了一个最大流问题。对于每条边，右边的数代表该边的最大流量，左边的数代表在最优解中，该边的实际流量。需要注意到，一个最大流问题的解可能不是唯一的。

对于一张给定的运输网络，Alice先确定一个最大流，如果有多种解，Alice可以任选一种；之后Bob在每条边上分配单位花费（单位花费必须是非负实数），要求所有边的单位花费之和等于P。

总费用等于每一条边的实际流量乘以该边的单位花费。需要注意到，Bob在分配单位花费之前，已经知道Alice所给出的最大流方案。现茌Alice希望总费用尽量小，而Bob希望总费用尽量大。我们想知道，如果两个人都执行最优策略，最大流的值和总费用分别为多少。

Hint:

\(n \le 100\)

Solution:

比较巧妙的一道题

第一问就是裸的最大流

对于第二位,考虑Bob的最优策略一定是全部对最大的那条边收费(这不显然吗)

所以我们要使最大边最小

二分答案,每次判断是否流没有减少

注意要实数二分,因为有这种情况:

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1 
#define rs p<<1|1
using namespace std;
typedef long long ll;
const int mxn=1e6+5;
int n,m,S,T,cnt,hd[mxn],cur[mxn],dep[mxn];
double mid,inf=10000000.0,eps1=1e-6,eps2=1e-9,ans,mxf;

inline int read() {
	char c=getchar(); int x=0,f=1;
	while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
	while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
	return x*f;
}
inline void chkmax(int &x,int y) {if(x<y) x=y;}
inline void chkmin(int &x,int y) {if(x>y) x=y;}

struct ed {
	int to,nxt; double trw,w; 
}t[mxn<<1];

inline void add(int u,int v,double w) {
	t[cnt]=(ed) {v,hd[u],w,w}; hd[u]=cnt++;
	t[cnt]=(ed) {u,hd[v],0,0}; hd[v]=cnt++;
}

int bfs() {
	memset(dep,0,sizeof(dep));
	queue<int > q; q.push(S); dep[S]=1;
	for(int i=0;i<=n+1;++i) cur[i]=hd[i];
	while(!q.empty()) {
		int u=q.front(); q.pop();// cout<<u<<"\n";
		for(int i=hd[u];i!=-1;i=t[i].nxt) {
			int v=t[i].to;
			if(dep[v]==0&&t[i].w-eps2>0.0) 
				dep[v]=dep[u]+1,q.push(v);
		}
	}
//	for(int i=1;i<=T;++i) cout<<i<<" "<<dep[i]<<"\n";
	return dep[T];
}

double dfs(int u,double f) {
	if(u==T) return f;
	for(int i=hd[u];i!=-1;i=t[i].nxt) {
		int v=t[i].to;
		if(t[i].w-eps2>0.0&&dep[v]==dep[u]+1) {
			double tp=dfs(v,min(f,t[i].w)); 
			if(tp-eps2>0.0) {
				t[i].w-=tp;
				t[i^1].w+=tp;
				return tp;
			}
		}
	}
	return 0;
}

void Dinic() {
	for(int i=1;i<=cnt;++i) if(t[i].to!=T&&t[i].to!=1) t[i].w=min(t[i].trw,mid);
	while(bfs()) {
		double tp=dfs(S,inf);
		if(tp>eps2) ans+=tp;
		else break ;
	}
}

int main()
{
	int u,v,p; double w; memset(hd,-1,sizeof(hd));
	n=read(); m=read(); p=read(); add(S,1,inf); T=n+1; add(n,T,inf);
	for(int i=1;i<=m;++i) {
		u=read(); v=read(); w=read();
		add(u,v,w); 
	} mid=500000.0; Dinic(); mxf=ans;
	double l=0.0,r=500000.0;
	while(r-l>eps1) {
		mid=(l+r)/2.0; ans=0.0; Dinic();
		if(mxf-ans<eps2) r=mid;
		else l=mid;
	}
	printf("%d\n%.4lf",(int)mxf,1.0*mid*p);
    return 0;
}