[JLOI2015]骗我呢

Description:

求一个n行m列矩阵的方案数,并满足限制:
1.对于任意\(x_{i,j} <x_{i,j+1}\)
2.\(x_{i,j}<x_{i-1,j+1}\)
3.\(0 \le x_{i,j} \le m\)

Hint:

\(n,m \le 10^6\)

Solution:

这题神了

先找下规律,由于要求行内单调,且受值域的限制,所以每行必有且仅有m-1个值

考虑在行之间转移

设\(dp[i][j]\)为第i行没有j的方案数

有 \(dp[i][j]=\sum_{k=0}^{k=j+1} dp[i-1][k]\) (手模显然)

再化简:

\(dp[i][j]=dp[i-1][j+1]+dp[i][j-1]\)

这个式子很像组合数

重点来了,我们"数形结合"一下:

其实就是这个

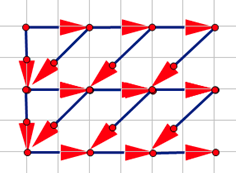
等价于

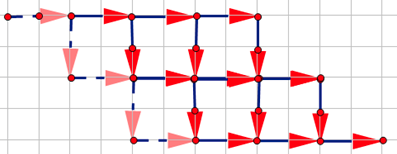
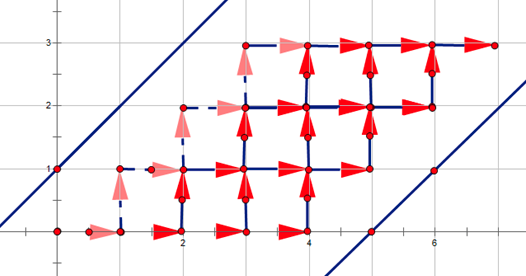
即求从原点走到(n+m+1,n)且不经过y=x+1和y=x-m-2的方案数

没有限制很好求,就是C(n+m+1+n,n)

考虑容斥

我们用总答案减去经过一条直线的,再加上经过两条直线的,再减去经过两条直线又绕回去的.......

就可以了

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1 
#define rs p<<1|1
using namespace std;
typedef long long ll;
const ll mxn=6e6+5,mod=1e9+7;
ll n,m,x,y,ans,cnt,hd[mxn],fac[mxn],ifac[mxn];

inline ll read() {
    char c=getchar(); ll x=0,f=1;
    while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
    while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
    return x*f;
}
inline void chkmax(ll &x,ll y) {if(x<y) x=y;}
inline void chkmin(ll &x,ll y) {if(x>y) x=y;}

struct ed {
    ll to,nxt;
}t[mxn<<1];

inline void add(ll u,ll v) {
    t[++cnt]=(ed) {v,hd[u]}; hd[u]=cnt;
}

inline ll C(ll x,ll y) {
    return 1ll*fac[x]*ifac[y]%mod*ifac[x-y]%mod;
}

ll qpow(ll a,ll b) {
    ll res=1,bs=a;
    while(b) {
        if(b&1) res=1ll*bs*res%mod;
        bs=1ll*bs*bs%mod;
        b>>=1;
    }
    return res;
}

inline ll cal(ll x,ll y) {
    return C(x+y,y);
}

void flip1(ll &x,ll &y) {
    --y; 
    swap(x,y);
    ++y;
}

void flip2(ll &x,ll &y) {
    y+=m+2;
    swap(x,y); 
    y-=m+2;
}

int main()
{
    n=read(); m=read(); fac[0]=ifac[0]=1;
    for(ll i=1;i<=max(n,m)*5;++i) fac[i]=1ll*fac[i-1]*i%mod;
    ifac[max(n,m)*5]=qpow(fac[max(n,m)*5],mod-2);
    for(ll i=max(n,m)*5-1;i>=1;--i) ifac[i]=1ll*ifac[i+1]*(i+1)%mod;
    x=n+m+1,y=n; ll ans=cal(x,y);
    while(x>=0&&y>=0) {
        flip1(x,y); ans=(ans-cal(x,y))%mod;
        flip2(x,y); ans=(ans+cal(x,y))%mod;
    }
    x=n+m+1,y=n; 
    while(x>=0&&y>=0) {
        flip2(x,y); ans=(ans-cal(x,y))%mod;
        flip1(x,y); ans=(ans+cal(x,y))%mod;
    }
    printf("%lld",(ans+mod)%mod);
    return 0;
}