BZOJ 3143 游走(贪心+期望+高斯消元)

一个无向连通图，顶点从1编号到N，边从1编号到M。 
小Z在该图上进行随机游走，初始时小Z在1号顶点，每一步小Z以相等的概率随机选 择当前顶点的某条边，沿着这条边走到下一个顶点，获得等于这条边的编号的分数。当小Z 到达N号顶点时游走结束，总分为所有获得的分数之和。 
现在，请你对这M条边进行编号，使得小Z获得的总分的期望值最小。

 

总分的期望值=每条边的期望经过次数*边的编号 之和。

不论我们如何编号，每条边的期望经过次数是不会变的，要使得边权和的期望最小，只需要贪心地使期望次数和边权倒序对应即可。 

考虑如何求每条边的经过次数，记每个点度数为di，期望通过次数为xi,每条边期望通过次数为yi则

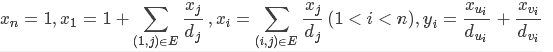
变形一下高斯消元即可。

 

# include <cstdio>
# include <cstring>
# include <cstdlib>
# include <iostream>
# include <vector>
# include <queue>
# include <stack>
# include <map>
# include <bitset>
# include <set>
# include <cmath>
# include <algorithm>
using namespace std;
# define lowbit(x) ((x)&(-x))
# define pi acos(-1.0)
# define eps 1e-8
# define MOD 1000000007
# define INF 1000000000
# define mem(a,b) memset(a,b,sizeof(a))
# define FOR(i,a,n) for(int i=a; i<=n; ++i)
# define FDR(i,a,n) for(int i=a; i>=n; --i)
# define bug puts("H");
# define lch p<<1,l,mid
# define rch p<<1|1,mid+1,r
# define mp make_pair
# define pb push_back
typedef pair<int,int> PII;
typedef vector<int> VI;
# pragma comment(linker, "/STACK:1024000000,1024000000")
typedef long long LL;
inline int Scan() {
    int x=0,f=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
inline void Out(int a) {
    if(a<0) {putchar('-'); a=-a;}
    if(a>=10) Out(a/10);
    putchar(a%10+'0');
}
const int N=505;
//Code begin...

struct Edge{int u, v; double w;}edge[N*N];
int dee[N], equ, var;
bool G[N][N];
double a[N][N], x[N];

int Guass(){
    int i, j, k, col, max_r;
    for (k=0,col=0; k<equ&&col<var; ++k,++col) {
        max_r=k;
        for (i=k+1; i<equ; ++i) if (fabs(a[i][col])>fabs(a[max_r][col])) max_r=i;
        if (fabs(a[max_r][col])<eps) return 0;
        if (k!=max_r) {
            for (j=col; j<var; ++j) swap(a[k][j],a[max_r][j]);
            swap(x[k],x[max_r]);
        }
        x[k]/=a[k][col];
        for (j=col+1; j<var; ++j) a[k][j]/=a[k][col];
        a[k][col]=1;
        for (i=0; i<equ; ++i) if (i!=k) {
            x[i]-=x[k]*a[i][col];
            for (j=col+1; j<var; ++j) a[i][j]-=a[k][j]*a[i][col];
            a[i][col]=0;
        }
    }
    return 1;
}
bool comp(Edge a, Edge b){return a.w>b.w;}
int main ()
{
    int n, m, u, v;
    scanf("%d%d",&n,&m);
    FOR(i,1,m) scanf("%d%d",&u,&v), G[u][v]=G[v][u]=true, ++dee[u], ++dee[v], edge[i].u=u, edge[i].v=v;
    equ=var=n-1;
    FOR(i,1,n-1) {
        if (i==1) x[i-1]=1;
        a[i-1][i-1]=1;
        FOR(j,1,n-1) {
            if (!G[i][j]) continue;
            a[i-1][j-1]=(-1.0)/dee[j];
        }
    }
    Guass();
    FOR(i,1,m) {
        u=edge[i].u; v=edge[i].v;
        edge[i].w=x[u-1]/dee[u]+x[v-1]/dee[v];
    }
    sort(edge+1,edge+m+1,comp);
    double ans=0;
    FOR(i,1,m) ans+=edge[i].w*i;
    printf("%.3f\n",ans);
    return 0;
}