有序表查找---斐波那契查找
注意:斐波那契查找的前提和折半查找和插值查找的条件相同,即待查找的查找表必须是顺序存储且有序。
斐波那契查找与折半查找很相似,他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1,及n=f(k)-1。
开始将key值与第f(k-1)位置的记录进行比较(及mid=low+f(k-1)-1),比较结果也分为三种
- key = a[mid]:mid位置的元素即为所求。
- key < a[mid]:high=mid-1,k-=1
high=mid-1说明待查找的元素在[low,mid-1]范围内,k-=1 说明范围[low,mid-1]内的元素个数为f(k-1)-1 个,f(k-1)-1是怎么求出来的呢? [low, mid-1]中元素个数为:high-low+1=mid-1-low+1=low+f(k-1)-1-1-low+1=f(k-1)-1。所以可以递归 的应用斐波那契查找。 - key > a[mid]:low=mid+1,k-=2
low=mid+1说明待查找的元素在[mid+1,hign]范围内,k-=2 说明范围[mid+1,high]内的元素个数为n - (f(k-1))= f(k)-1-f(k-1)=f(k)-f(k-1)-1f(k-2)-1个,所以可以递归的应用斐波那契查找。
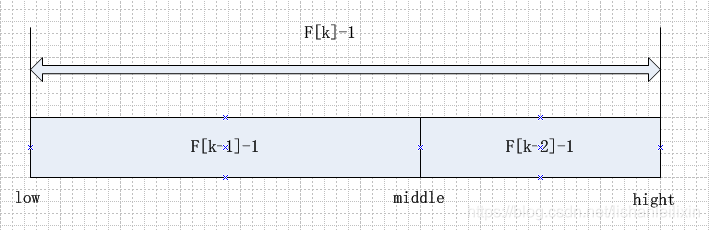
n=f(k)-1是为什么?
是为了格式上的统一,以方便递归或者循环程序的编写。表中的数据是f(k)-1个,使用mid值进行分割又用掉一个,那么剩下f(k)-2个。正好分给两个子序列,每个子序列的个数分别是f(k-1)-1与f(k-2)-1个,格式上与之前是统一的。不然的话,每个子序列的元素个数有可能是f(k-1),f(k-1)-1,f(k-2),f(k-2)-1个,写程序会非常麻烦。
代码如下(Java):
import java.util.Arrays;
public class FibonacciLookup {
public int max_size = 20;
public int[] f;
public FibonacciLookup(int max_size) {
this.max_size = max_size;
this.f = new int[this.max_size];
}
public FibonacciLookup() {
this.f = new int[this.max_size];
}
public void Fibonacci() {
this.f[0] = 0;
this.f[1] = 1;
for (int i = 2; i < this.max_size; i++) {
this.f[i] = this.f[i - 1] + this.f[i - 2];
}
}
public int Fibonacci_Search(int[] a, int n, int key) {
int low = 0, high = n - 1, mid;
int k = 0;
this.Fibonacci();
while(n > (this.f[k] - 1)) {
++k;
}
int[] temp = Arrays.copyOf(a, this.f[k] - 1);
for (int i = n; i < temp.length; i++) {
if(i >= n) {
temp[i] = temp[n - 1];
}
}
while(low <= high) {
mid = low + this.f[k - 1] - 1;
if(key < temp[mid]) {
high = mid - 1;
k=k-1;
}
else if(key > temp[mid]) {
low = mid + 1;
k = k-2;
}
else {
if(mid <= high) {
return mid;
}
else {
return high;
}
}
}
return -1;
}
public static void main(String[] args) {
int[] a = {1, 16, 24, 35, 47, 59, 62, 73, 88, 99};
FibonacciLookup f = new FibonacciLookup();
System.out.println(f.Fibonacci_Search(a, 10, 59));
}
}



