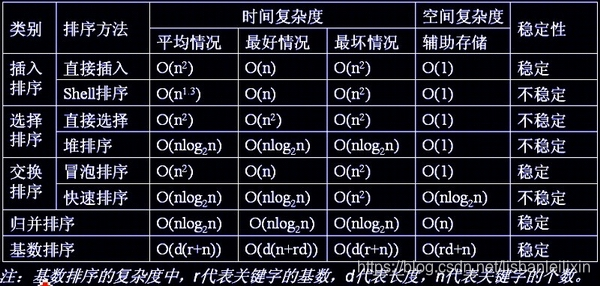
堆排序(最大堆)的理解和实现(Java)

堆的定义

堆是具有下列性质的完全二叉树：每个节点的值都大于或等于其左右孩子节点的值，称为大顶堆；或者每个节点的值都小于或等于其左右孩子的值，称为小顶堆。如下图举例：

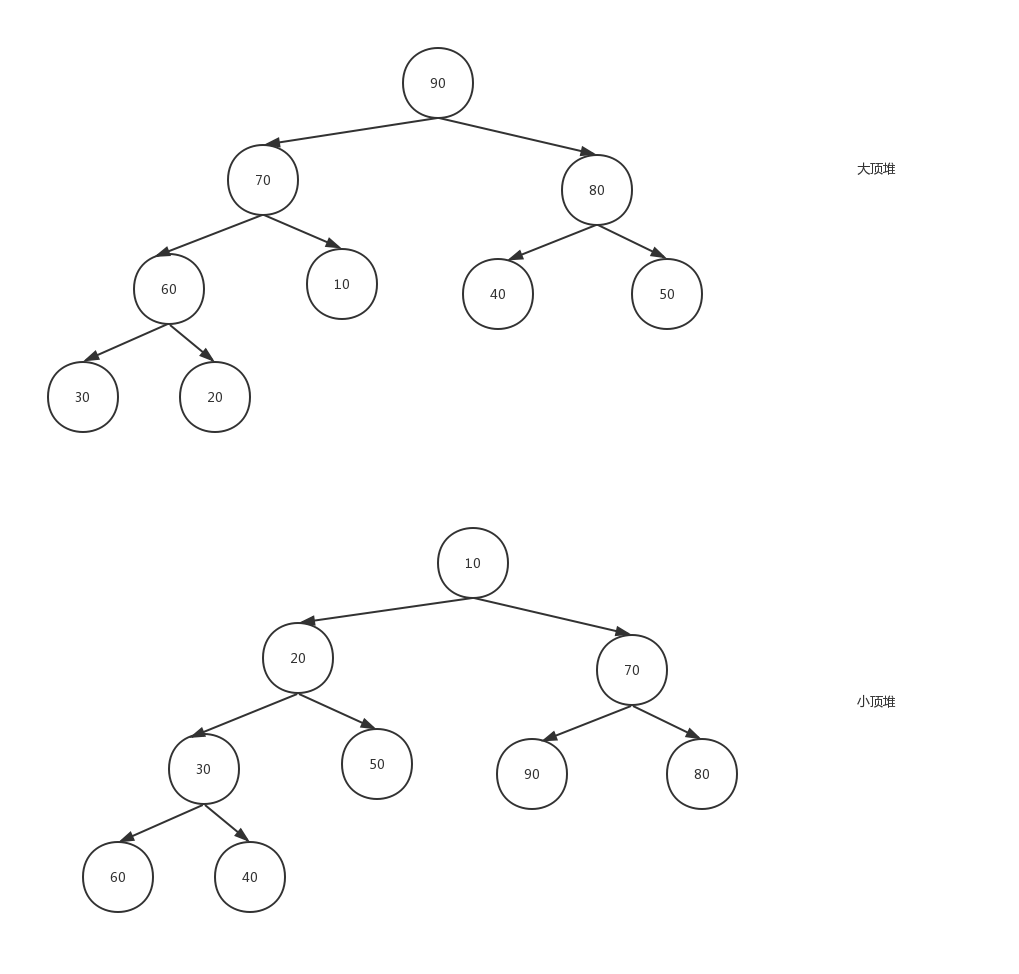
通过堆的定义可知，根节点一定是对中所有节点的最大(小)值。较大(小)的节点靠近根节点(并不绝对，比如上图小顶堆中60, 40均小于70，但它并没有70靠近根节点)
按层序方式给节点从1开始编号，则节点之间满足下列关系:
$\left \{\begin{array}{cc} k_i \geq k_{2i}\\ k_i \geq k_{2i+1} \end{array}\right.$
或：
$\left \{\begin{array}{cc} k_i \leq k_{2i}\\ k_i \leq k_{2i+1} \end{array}\right.$
其中i满足：1 $\leq$ i $\leq$ $\frac{n}{2}$

这里i为什么小于等于 $\frac{n}{2}$呢？
根据完全二叉树的性质，对于一棵完全二叉树，如果某一个节点的下标i=1，则这个节点是二叉树的根，无双亲；如果i > 1，则其双亲是节点$\frac{i}{2}$。那么对于有n个节点的二叉树来说，它的i值自然就是小于等于$\frac{n}{2}$了。

堆排序算法原理

堆排序(Heap Sort)就是利用堆(这里我们假设利用的最大堆，最小堆类似)进行排序的方法，它的基本思想就是，将待排序的序列构造成一个大顶堆。此时整个序列的最大值就是堆顶的根节点。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中次大值，如此反复执行，就能得到一个有序序列。

算法流程：

1. 将含有n个元素的待排序的序列 ($r_1$, $r_2$, $r_3$, …, $r_n$) 初始化成一个大顶堆，此堆为初始的无序区。
2. 将堆顶元素r[1]和最后一个元素r[n]进行交换，交换完成后得到新的无序区：($r_1$, $r_2$, $r_3$, …, $r_{n-1}$)，和一个新的有序区 ($r_n$)。
3. 交换后的新的堆顶元素r[1]可能破坏堆的性质，所以重新将当前无序区调整为一个新堆。然后再将堆顶元素r[1]和无序区最后一个元素进行交换，得到一个新的无序区 ($r_1$, $r_2$, …, $r_{n-2}$)和一个新的有序区 ($r_{n-1}$, $r_n$)。
4. 重复上述过程，直到有序区的元素个数为n-1，整个排序过程完成

举例说明：
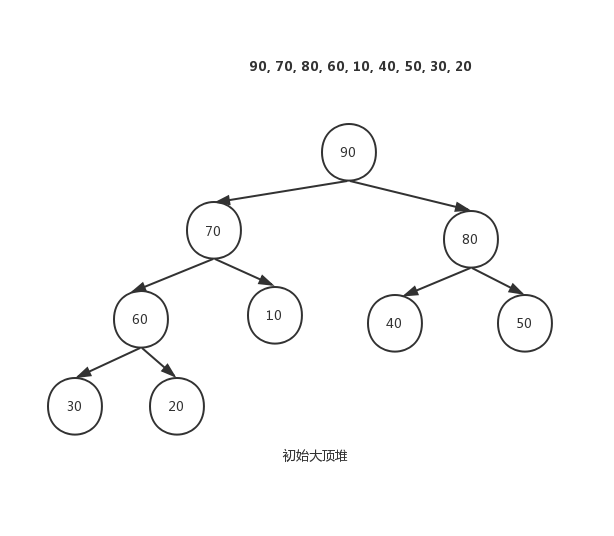
假设我们要排序的序列是{50, 10, 90, 30, 70, 40, 80, 60, 20}，长度为9
将待排序序列初始化为一个堆：

则堆排序过程如下：

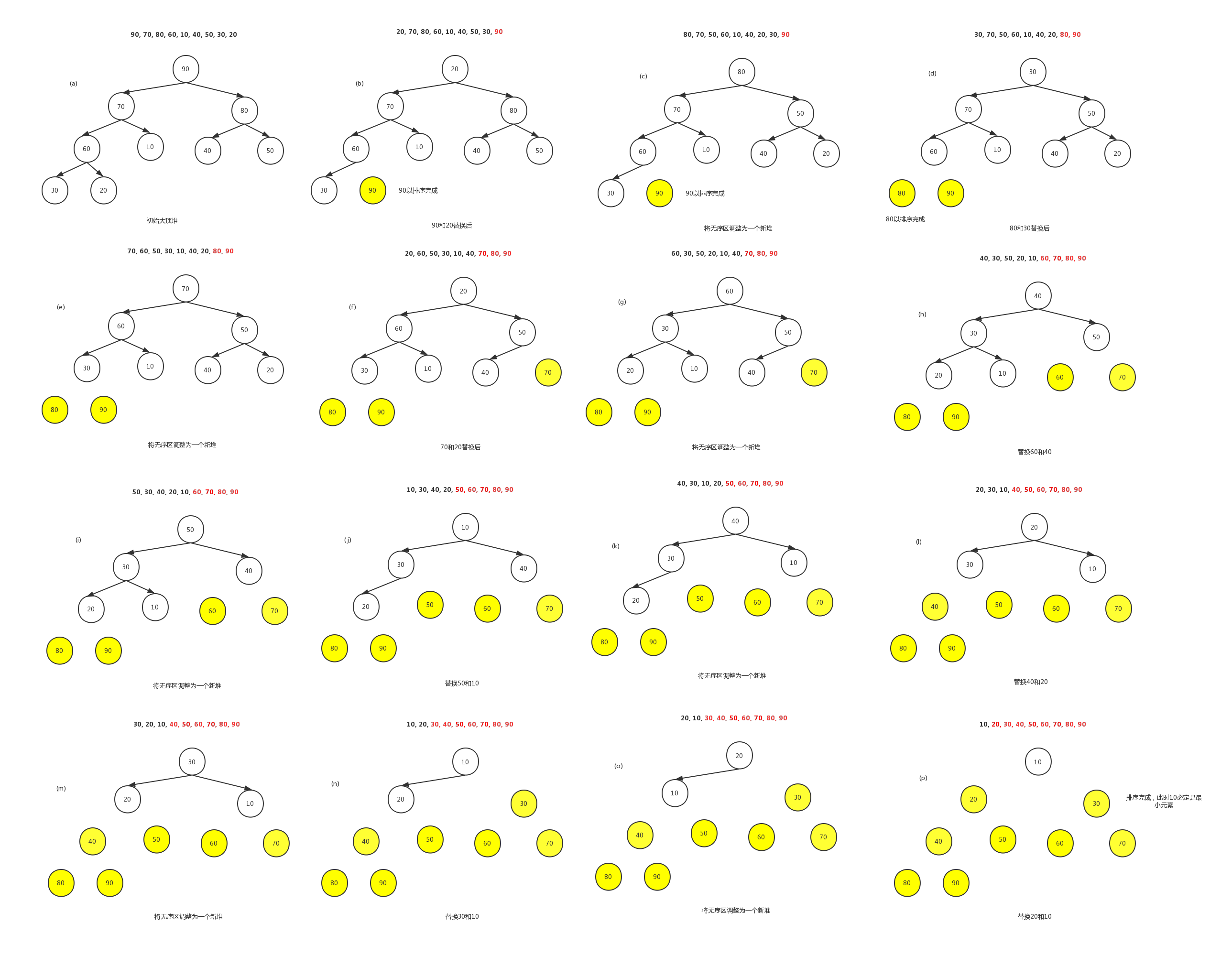
(ps：画图一度画疯…)

现在我们了解了堆排序的过程，但是还有两个问题：

1. 如何减肥一个无序序列构建成一个堆？
2. 如何在输出堆顶元素后，调整剩余元素成为一个新的堆？

我们所谓的将待排序的序列构造成一个大顶堆，其实就是从下往上、从右到左，将每个非终端(非叶子节点)节点当做根节点，将其和其子树调整成最大堆。
具体看代码：

public class MaxHeapSort {

	/**
	 * 已知elem[s....m]中记录的关键字除elem[s]之外满足堆的定义
	 * 本函数调整elem[s]的关键字，使elem[s.....m]成为一个大顶堆
	 * @param elem
	 * @param s
	 * @param m
	 */
	public void maxHeapAdjust(int[] elem, int s ,int m) {
		int temp, j;
		temp = elem[s];
		for (j = 2 * s; j <= m; j *= 2) {  //沿关键字较大的孩子节点向下筛选
			if(j < m && elem[j] < elem[j + 1]) {  //判断左孩子大还是右孩子大
				++j;                    //j为关键字中较大的下标
			}
			if(temp >= elem[j]) {
				break;
			}
			elem[s] = elem[j];
			s = j;
		}
		
		elem[s] = temp;   //插入
	}
	
	public void swap(int[] elem, int i, int j) {
		int temp = elem[i];
		elem[i] = elem[j];
		elem[j] = temp;
	}
	
	/**
	 * 对顺序表elem进行堆排序
	 * @param elem
	 */
	public void maxHeapSort(int[] elem) {
		int length = elem.length - 1;
		for (int i = length / 2; i > 0; i--) {  //把elem构建成一个大顶堆
			maxHeapAdjust(elem, i, length);
		}
		
		for (int i = length; i > 1; i--) {
			swap(elem, 1, i);    //将堆顶记录和当前未经排序子序列的最后一个记录交换
			maxHeapAdjust(elem, 1, i - 1);  //将elem[1.....i-1]重新调整为一个大顶堆
		}
	}
	
	public static void main(String[] args) {
		MaxHeapSort m = new MaxHeapSort();
		int[] elem = {0, 50, 10, 90, 30, 70, 40, 80, 60, 20};
		m.maxHeapSort(elem);
		
		for (int i = 1; i < elem.length; i++) {
			System.out.print(elem[i] + ", ");
		}
	}
}

输出：

10, 20, 30, 40, 50, 60, 70, 80, 90, 

堆排序复杂度分析

堆排序的运行时间主要是消耗在初始构建堆和重建堆时的反复筛选上。
在构建堆的过程中，因为我们是完全二叉树从最下层最右边的非终端节点开始构建，将它和其孩子进行比较和若有必要的交换，对于每个非终端节点来说，其实最多进行两次比较和互换操作，因此真个构建堆的时间复杂度是O(n)。
在正式排序时，第i次取堆顶记录重建堆需要用O(logi)的时间 (完全二叉树的某个节点到根节点的距离是[$log_2$i] + 1)，并且需要取n-1次堆顶记录，因此重建堆的时间复杂度为O(n$\log$n)。
所以堆排序的整体时间复杂度为O(n$\log$n)。由于堆排序对原始记录的排序状态并不敏感，因此无论是最好，最坏和平均时间复杂度均为O(n$\log$n)。
空间复杂度上，只有一个用来交换的暂存单元，但是由于记录的比较与交换是跳跃式进行的，因此堆排序也是一种不稳定的排序方法
另外，由于初始构建堆所需的比较次数比较多，因此他不适合待排序序列个数较少的情况。