剑指：构建乘积数组

题目描述

给定一个数组 A[0, 1, …, n-1]，请构建一个数组 B[0, 1, …, n-1]，其中 B 中的元素 B[i]=A[0]×A[1]×… ×A[i-1]×A[i+1]×…×A[n-1]。

不能使用除法。

样例

输入：[1, 2, 3, 4, 5]

输出：[120, 60, 40, 30, 24]

思考题：

• 能不能只使用常数空间？（除了输出的数组之外）

 

解法

把 B 的每个元素 B[i] 看成两半的乘积，即 A[0]xA[1]x...xA[i-1] 和 A[i+1]xA[i+2]xA[n-1]。

• 对于左半部分：B[i] = B[i - 1] * A[i - 1]

即是说：

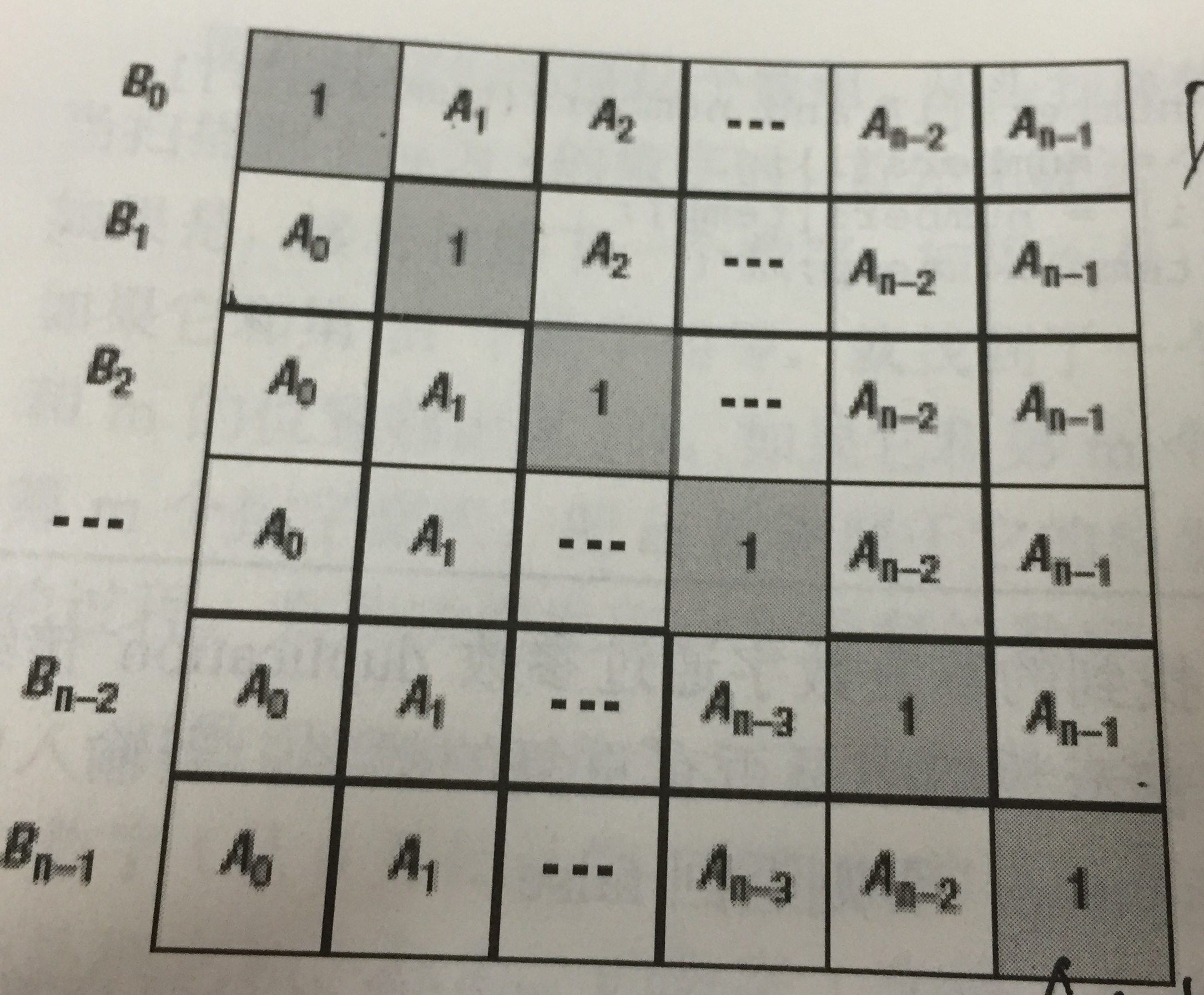
B[i]的值可以看作下图的矩阵中每行的乘积。

下三角用连乘可以很容求得，上三角，从下向上也是连乘。

因此我们的思路就很清晰了，先算下三角中的连乘，即我们先算出B[i]中的一部分，然后倒过来按上三角中的分布规律，把另一部分也乘进去。

 

 

public class Solution {
    public int[] multiply(int[] A) {
        if(A==null||A.length<1){
            return A;
        }
        int n = A.length;
        int[] B = new int[n];
        B[0] = 1;
        for(int i=1; i<n; i++){
            B[i] = B[i-1] * A[i-1];
        }
        int t = 1;
        for(int j=n-2;j>=0; j--){
            t *= A[j+1];
            B[j] *= t;
        }
        return B;
    }
}