剑指：旋转数组的最小数字

旋转数组的最小数字

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

输入一个升序的数组的一个旋转，输出旋转数组的最小元素。

例如数组 {3,4,5,1,2} 为 {1,2,3,4,5} 的一个旋转，该数组的最小值为 1。

数组可能包含重复项。

注意：数组内所含元素非负，若数组大小为 0，请返回 -1。

样例

输入：nums=[2,2,2,0,1]

输出：0

解法

解法一

直接遍历数组找最小值，时间复杂度 O(n)，不推荐。

class Solution {

    /**
     * 获取旋转数组的最小元素
     *
     * @param nums 旋转数组
     * @return 数组中的最小值
     */
    public int findMin(int[] nums) {
        if (nums == null || nums.length == 0) {
            return -1;
        }
        int min = nums[0];
        int n = nums.length;
        if (min < nums[n - 1]) {
            return min;
        }
        for (int i = 1; i < n; ++i) {
            min = Math.min(min, nums[i]);
        }
        return min;
    }
}

 

解法二

思想：

首先，旋转后的数组实际可以划分为两个排序的子数组，而最小的元素刚好是这两 个子数组的分界线(第二个子数组的首位)。而且前面的子数组的元素都大于或等于后面的子数组的元素。

在排序数组中可以用二分查找实现O(logn)的查找。

所以我们可以通过二分查找的思路来寻找这个最小的元素。

 

算法：

利用指针 start,end 指向数组的首尾，如果 nums[start] < nums[end]，说明数组是递增数组，直接返回 nums[start]。否则进行如下讨论。

计算中间指针 mid：

• 如果此时 nums[start], nums[end], nums[mid] 两两相等，此时无法采用二分方式，只能通过遍历区间 [start,end)获取最小值；
• 如果此时 start,end 相邻，说明此时 end 指向的元素是最小值，返回 nums[end]；
• 如果此时 nums[mid] >= nums[start]，说明 mid 位于左边的递增数组中，最小值在右边，因此，把 start 指向 mid，此时保持了 start 指向左边递增子数组；
• 如果此时 nums[mid] <= nums[end]，说明 mid 位于右边的递增数组中，最小值在左边，因此，把 end 指向 mid，此时保持了 end 指向右边递增子数组。

 

执行过程图示例：(阴影部分为第二个子数组)

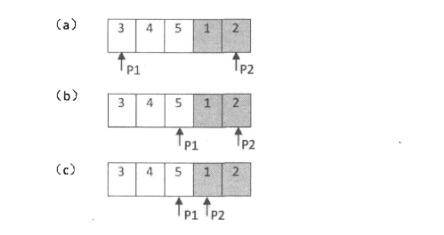
(a) 把p1指向数组的第一个数字，p2指向数组的最后一个数字。中间数字5大于p1指向的数字(递增)，所以中间的数字在第一个子数组中。下一步把p1指向中间的数字。

(b) p1和p2中间的数字1小于p2指向的数字，中间的数字在第二个子数组中。下一步把p2指向中间的数字(最小值在第二子数组首位，向左靠)。

(c) p1和p2指向两个相邻的数字，则p2指向的数组中的最小数字。

 

特殊情况：

在这两个数组中，第一个数字、最后一个数字和中间的数字都是1(相等)，无法确定中间的数字1属于第一个递增子数组还是第二个。

public class Solution {
        
    public static int findMin(int[] nums){
        if(nums==null || nums.length==0) return -1;
        
        int start=0, end=nums.length-1;
        
        if(nums[start] < nums[end]) return nums[start]; //旋转了0个元素的情况
        
        int mid = 0;
        while(nums[start] >= nums[end]){//前面的子数组的元素都大于或等于后面的子数组的元素
            if(end-start==1){ 
                mid = end;
                break;
            }
            mid = (start + end)/2;
            
            if(nums[start] == nums[end] && nums[mid] == nums[start]){ //start、end、mid均相等，则只能顺序查找了
                return findMin(nums, start, end);
            }
            
            if(nums[mid]>=nums[start]) //在第一个子数组
                start = mid;
            else if(nums[mid]<=nums[end]) //在第二个子数组
                end = mid;
        }
        
        return nums[mid];
    }
     
    private static int findMin(int[] nums, int start, int end) {
        int min = Integer.MAX_VALUE;
        for(int i=start;i<end;i++)
            min = Math.min(min, nums[i]);
        return min;
    }

    public static void main(String[] args) {
        int[] nums = {3,4,5,1,2,3};
        int[] nums1 = {1,0,1,1,1};  
        int[] nums2 = {1,1,1,0,1};  
        System.out.println(findMin(nums1));
    }
}